Word-Classes in automatic syntactic analysis

Jacob Mey (Oslo)

[Články]

(pdf)

Slovní druhy v automatické syntaktické analýze / Классы слов в автоматическом синтаксическом анализе / Classes des mots dans l’analyse syntaxique automatique

[*]Introduction. In a very unsophisticated interpretation, word-classes are nothing else than classes of words. The problem is to delimitate those classes, ie., to find criteria for establishing subsets of the set of all words of a language. (Another problem is to define the concept of word, but we are not concerned with this issue here.)

There have been attempts to classify the words of a language on a purely semantical basis, as in Ancient and Medieval grammar, the so-called classical school grammar, and, in a more refined form, in Brøndalʼs work on word-classes.[1]

Other, more recent approaches have taken their starting point in what one might term very broadly as a distributional view of linguistic classification. This approach, based on the concepts of narrow and wide environments, is represented by such [221]scholars as Bloomfield and Wells[2] among many others. The question what comes first, morphology or syntax, and, consequently, which criterion should be considered primary, has been answered in mainly two different ways, neither of them quite satisfactory. One way is to accept the basic paradox of definitory circularity by incorporating the circularity itself into the definiton; another, to abolish the paradox by blurring, or lifting the boundaries between syntax and morphology altogether. Both alternatives have been proposed and/or accepted: the first one is implicit in most American structural descriptions of the last thirty years, and is occasionally made explicit in works of more theoretical nature;[3] the second has its most outspoken advocates in linguists like Nida, Pike and Harris.[4] As far as European linguistics is concerned, the glossematic position is well known, and coincides with the second alternative of American linguistics.[5] Some of the ideas presented by members of the Prague School give rise to interesting implications that until recently have not been taken into account; I will comment on this in the following sections.

Syntactic and morphological word-classes. From what has been said above, it follows that there are mainly two ways of approaching the problem of word-classes. One can define word-classes on a purely morphological basis: the classical division of words into “parts of speech” (but without its semantic implications) can be interpreted in terms of morphological differences between classes of words (e. g. in English: nouns, verbs, adverbs and the like). It has been often remarked, and should go without saying, that these kinds of word-classes are hard to define on a general linguistic basis: but some generalization can, of course, be made (such as the use of the term “noun” for the German Mensch as well as for the French homme and so on). It should be noted that the so-called commutation test (or substitution test, in American linguistic parlance) aims at the establishment of morphological word-classes, even though the test in itself is basically independent of the choice of the criterion of morphology. The syntactical relations of glossematics are thus established on a purely morphological basis; this adds to precision but detracts from generality.

On the other hand, one can take oneʼs starting point in syntax, and from there on try to define the word-class. Using the commutation technique, but taking as oneʼs basis the syntactical concepts of subject, predicate etc., one can establish the notion of “syntactic word” as done e. g. by Šmilauer.[6] In this way one defines a class of words or word-like elements that can figure in the same environments as some given word, or, in other terms, that can play the same syntactic role as a given word. Thus, a number word, a pronoun, an infinitive etc. can play the same parts in the sentence as can the noun, that is, they can be subjects, objects etc. In this way we determine a class of “syntactic nouns”. It is important that the basic concept here is not that of noun as such, but of the syntactic role. This concept will be analyzed in detail in the following.

[222]But one need not tie oneself up with the narrow interpretation of the commutation test that is usually accepted. The glossematic approach, often criticized for its lack of broadmindedness, has suffered more by the scholasticity of its followers than by the attacks of its adversaries. Why should the “test” be confined to the word as such, why not widen the frame to comprise not words, but rather “places” or “fields”? One of the most successful attempts to define syntactic roles in these terms rather than in terms of individual words, is that by Paul Diderichsen.[7] His idea is to „choose certain fixed members in the totality (of the sentence, JM) as point of departure for the position rules“. In recent years, Diderichsenʼs ideas have been fruitfully and originally developed by Hans Karlgren[8] in the direction of a quantitative mathematical model. Important to notice are two main differences from the “syntactic word” approach: (1) the “places” (fields, positions) do not concern only words, but also (and more often) groups, i.e. sequences of words;[9] (2) the positions are non-homogeneous as to morphological characteristics of the words that occupy them (by this I mean that they may contain homogeneous words, but they need not do so). I have thus introduced two important concepts: syntactic word class and syntactic role. We will need both in what follows; a more precise definition will have to wait. First of all, we will have to examine the concept of word-class as it is used in automatic syntactic analysis (ASA), as indicated by the title of this paper.

Word-classes in ASA. Automatic syntactic analysis can be characterized as a method for establishing a transition (in a finite number of steps) from the actual string (the “process”, in glossematic parlance) to the structure “behind” it (the “system”[10]). In order to establish an effective procedure, one has to start with a certain corpus of well-formed sentences (strings of words). The first step in a predictive system like that developed by Kuno and Oettinger[11] is to replace the elements of the string (the words) by the categories (the word-classes) to which they belong. We can obtain an extensional definition of any word-class by looking up the rules with a certain word-class symbol at their right hand side in some kind of reverse dictionary (like that provided in Appendix B of Kuno 1963b). Supposing that the dictionary is complete, and that there are no homographs, the word-classes established in this manner will induce a partition on the set of all words.

Furthermore, if I want to define the word-classes intensionally, I must look for some defining properties in the realm of syntactics. In the categorial [223]grammar as developed by e.g. Lambek, the syntactic properties of the categories are very neatly described and clearly symbolized in the cancellation rules (note that there is a certain interplay between dictionary entry — “type assignment” — and grammar rule[12]). In Kuno and Oettingerʼs much more elaborate predictive analysis procedure the syntactic properties are bound up with the concept of prediction: each word (or rather, the class it represents) taken together with its precedessor gives rise to a number of possible constructions (“predictions”); some of these may combine successfully with the next word, and so on, until I have obtained one or more successful parsings of the whole sentence. A prediction is nothing else than a possible structure, i.e. a possible continuation of the string of category symbols established so far. The only purpose of the categories is thus to enable us to make predictions. These should be “as general as possible until it becomes compulsory to make them specific” (Kuno and Oettinger, I-7): the assignment of word-class symbols to words should comprise every possible structure in which the word and its (possible) successors can occur. So, if we want to determine the intension of a word-class, we must ask: in what rules can this word-class occur, or (which amounts to the same): what kind of predictions can I establish on the basis of this particular word, viewed on the background of preceding words or structures, its own syntactic role(s), and possibly (e.g. in the case of homographs) its semantic content. Note that the traditionally emphasized criterion of morphological shape does not explicitly enter into the criterion, but only insofar as it allows us to make some statement about some of the other points. Thus, morphological differences in words belonging to the same root (like conjugation forms of the verb) do not constitute a sufficient (and sometimes not even a necessary) condition for establishing a word-class. Languages with explicit morphological indication of syntactic roles (such as Latin, most Slavonic languages) will be inclined to put more emphasis on the morphological differences than does English, where the syntactic roles more often than not are manifested independently of (word) morphology. The intension of the category thus corresponds, in an informal way, to all possible structures that can be predicted on the basis of: (1) the symbol itself; (2) its syntactic role; (3) its preceding structure (prediction).

The following is an attempt to formalize these notions and their relations in a way that is mainly dependent on the characterization of the grammatical matching function in Oettinger and Kuno, I-6. The angle of approach, however, is different, since we are interested in the theoretical implications of the definitions (especially that of syntactic word class), and their practical interpretation in terms of linguistic entities. Besides the system is somewhat idealized, cf. below.

An (automatic) syntactic analysis system is considered as a sextuple ⟨S, P, P*, R, G, Q⟩ where:

S: a non-empty finite set of syntactic word-class symbols s₁ … s_m;

P: a non-empty finite set of grammatical prediction symbols p₁ … p_n;

R: a non-empty finite set of syntactic role indicators r₁ …r_q;

[224]S, P and R are disjoint sets.

G, Q: two binary relations, to be defined in the following.

An associative concatenation operation is defined on the set P, such that we obtain a free semigroup P containing all possible strings of p_i ∊ P (prediction symbols). P* is a subset of P, containing the “marked” strings on P (marked in a sense akin to that of Kulagina;[13] p^*₁ … p^*_r ∊ P*.

Now we define Q (p^*) = r, ie. Q is represented by the set of ordered couples ⟨p^*, r⟩: Q maps P* onto R; consequently, for every p^*_j ∊ P* we have one and only one r_k ∊ R (but each r_k can have several p^*_j ∊ P*).[14]

The relation G is now defined as follows:

Let A, a non-empty finite set of arguments, (or argument pairs, more correctly) be defined as the direct (Cartesian) product of P and S: A = P × S, a_l ∊ A, the set of all couples (p, s). Let now ⟨p^*, r⟩ be symbolized by q; q_s, ∊ Q, a subset of P* × R. Then we define G (q) = a, i.e. the extension of this relation G is the set of ordered couples ⟨q, a⟩. Again, since for every q_s there is only one a_l, while for every a_l we have one or several q_s, we have a mapping onto.

Before we go any further, remark the following:

A is to be taken as P × S, and not P* × S.

This is because the pushdown store mechanism that operates in connection with the analysis, gives us only a p ∊ P (ie. a single prediction symbol at a time), and not a p^* ∊ P* (ie. a string of predictions, or, if one prefers, a structure). Now, according to my interpretation of the mapping G, together with the definition of a mapping onto, there should be at least one element in the definition set for every element in the value set. This means that there should be no a ∊ A that do not correspond to some q ∊ Q. However, under a given concrete linguistic interpretation of the formalism, it is to be expected that some of the argument pairs do not have a corresponding structure in Q (unless we introduce a zero element in Q into which all „incompatible“ argument pairs map). This problem will be discussed in the next paragraphs.

According to Kuno and Oettinger (l.c.), the mapping is not from the set Q into the argument set: instead, they define a binary relation G' (a) = q (for every a ∊ A), that is not a function at all. In fact, we have (I use the symbolism introduced here, to save space and for greater convenience), for example:

Let A be {a₁, a₂, a₃, a₄, a₅}.

Let Q be {q₁, q₂, q₃, q₄}. To this set we add q₀, the zero element, and call the new set Q'. Next, we set up the following correspondences between elements of A and elements of Q' (called rules, resp. subrules of the grammar under the interpretation):

 

Fig. 1

 

[225]If we look at the above table together with the corresponding graphical representation (Fig. 1), we easily see that we have fulfilled the conditions put by Kuno and Oettinger (l.c.):[15] “To each ordered argument pair (P_i, S_j), G assigns a set, possibly empty, of ordered pairs . Each element of G (P_i, S_j) corresponds to a set of structures that may follow when the syntactic structure represented by the given prediction P_i is initiated by a word belonging to class S_j. Whenever P_i and S_j are grammatically incompatible, G (P_i, S_j) = ∅, the empty set.” On the other hand, G' is not a unique mapping, because it does not assign a unique value in Q' for each a ∊ A.[16] (We cannot formally object to the fact that in some cases G' (a₁) = ∅, ie. maps into the zero element). Moreover, we have not fulfilled our own condition above: “for every q_s we have only one a_q”. This condition says that every particular couple in Q' may be generated only by one argument pair. Superficially speaking, this seems to be an unnecessary complication: cannot one and the same structure be generated by different argument pairs? This is, seemingly, also in accordance with Kuno and Oettinger, l.c. who talk about the elements of G' (S_i, P_j) as “structures”, and structures (taken as strings of prediction symbols) may of course be generated by different argument pairs. However, if we limit the use of the term structure (as I have done) to the elements of the set P, the elements of Q do not contain sets of structures, but are rather pairs consisting of one structure plus one syntactic role indicator each. For these couples, the relation to the argument pairs is not far from being unique, as one can verify in the interpretation, ie. the grammar table, by comparing syntactic roles and new predictions (structures) to their corresponding argument pairs.[17] In order to obtain uniqueness from Q to A, we have to correct our example for instance in the following way: take out the couples (a₂, q₂), (a₅, q₄), and delete the corresponding lines in the diagram. Thus we get the following graphical representation:

 

Fig. 2

 

Now we see that apart from the dual representation of q₀ in A, the set Q' qualifies for uniqueness with respect to A: to every q corresponds a unique a (the requirement for a function). The closest we can come to a unique mapping is to exchange the sets A and Q with respect to the relation G, taking Q' as the definition set and A as the value set. As seen from Fig. 2, the only hindrance is the existence of the element q₀. On the other hand, the set A is far too large for our purposes: what we really need is a set of “marked” arguments (in the sense mentioned above) A* ⊂ A. Both problems are taken care of in the following way:

[226]We know Q to be a subset of Q', since we obtained Q' by adding p₀ to Q.[18] Now, we look for the images of Q in the set A: wee se that we have a mapping of Q into A (Fig. 3).

If we ask ourselves how this mapping was obtained, the answer is: by taking out the zero element q₀ in the set Q', ie., by destroying all the couples with the second coordinate q₀ in the table of Fig. 2. By doing this, we automatically obtain the set A*, a subset of A, for whose elements we have images in Q; the mapping

 

Fig. 3

 

Q → A will be a mapping onto: G (Q) = A*. This set of all marked arguments is thus obtained by logical construction; the result is shown in Fig. 4.

 

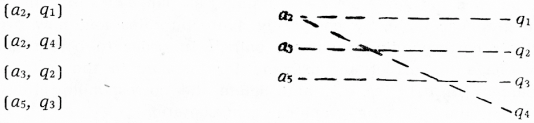
Fig. 4

 

I will now turn to the original question; how to determine the intension of the concept of “syntactic word class” (SWC)? It should be kept in mind that my concept of SWC is not exactly coincident with Kuno and Oettingerʼs, because of the idealization introduced above.) Basing ourselves on the formal characterization given in the preceding paragraphs, it is not difficult to see what the SWC “does”: together with a given (old) prediction, it forms a unique argument pair corresponding to every couple that consists of a given syntactic role indicator (SRC) and a given (new) prediction. The following will be an attempt to give a concrete linguistic interpretation of the formalism, following, as close as possible, that developed in Kuno and Oettinger, Kuno 1936a and b, but trying to make the interpretation more explicit, while keeping it in accordance with the formalism presented here.

The sets S, P and R are disjoint sets, ie. they have no members in common. Under the interpretation, however, we can have the same interpretata for some of the members of some or all of the classes. E.g. the symbol PRD (∊ S) and PD (∊ P) have the same interpretation PERIOD (.). TIT (∊ S) and TI (∊ R) are both interpreted as TEMPORARY SUBJECT. And so on. This should cause no difficulties, since the symbols (the members of S, P, R) are different.

[227]Another question is: what do these symbols represent in terms of words, strings of words, parts of speech, phrases etc.?

S, the set of SWC symbols, is represented by words (typographical): for every word there is at least one SWC. Appendices A and B of Kuno 1963b give SWC sorted by words (alphabetically) and words sorted by SWC, respectively. The list of SWC is given in Kuno 1963a as a fold-out. There are 133 SWC. Typical members (described in full in Appendix A of Kuno 1963a) are: ADJECTIVE 1 through 7, AUXILIARY VERB, COMMA, HAVE-TENSE AUX, INFINITE VT 1 through 7, PREPOSITION, PAST P OF VT 1 through 7, TO FOR INFINITIVE, SINGLE OBJECT VT, COORDINATE CONJ 1 and 2.

P, the set of prediction (P) symbols, is represented by predictions, ie. roughly speaking, possible structures in the language. Note that although the set P consists of single symbols, the interpretation is by no means restricted to single words for single symbols or vice versa. A structure of words may correspond to one prediction symbol (like S for SENTENCE); a symbol may correspond to a single “word” (like PD for PERIOD (.)). Briefly, the predictions characterize abstract structures, not concrete (strings of) words. There are 82 predictions in the system, apart from the suffixed predictions (used to specify more closely when needed): e.g. NC stands for NOUN CLAUSE, NC-C for SUBJECT CLAUSE, NC-D for OBJECT CLAUSE and so on. The prediction table is found in Kuno 1963a, II-15, the subclassified predictions ib., 18—24. Unsuffixed predictions are used in argument pairs and new predictions, suffixed prediction symbols only in argument pairs. Typical members are: SUBJECT, THANCLAUSE, PREPOSITIONAL PHR, NOUN CLAUSE, AUXILIARY VERB, ADVERB, GERUND, RELATIVE PRONOUN ACC, PARTICIPLE.

R, the set of syntactic role (SRC or SR) symbols, is represented by the syntactic role played by the words, whose classes figure as second coordinates of the argument pairs of the grammar rules in question. The 32 SRC symbols are found in Kuno 1963a, II-32. Typical members are: ADVERB, ADVERBIAL NOUN PHRASE, END OF CLAUSE, END OF SENTENCE, IMPERATIVE VERB, OBJECT, PREDICATE VERB, SUBJET OF PREDICATE VERB. The interpretation of the SRC is not without difficulties. There is a marked difference in the frequency of their use: about 1/4 of them are used only once or twice (two symbols CN, SN, occurring only in one rule each, are not defined or mentioned at all in the SRC Table or the text); the most frequently used codes are those that correspond to the traditional concepts of sentence analysis such as SV (SUBJECT OF PREDICATE VERB), PR (PREDICATE VERB) and the like. Now, SRC do not only concern words, but also, in many cases, groups of words (cp. Kuno 1963b, I-100). Assigning an SRC to an SWC corresponding to a word that is the beginning of a group of words entails the necessity of assigning the role code to the rest of the structure, ie. to the whole of the new prediction, as well. (See the relevant discussion on “mixing of levels” as compared to a generative grammar, Kuno 1963b, I-103-4). The SRC gives in this case additional information about the structure to follow, ie. the new prediction; and this information is not always contained in the prediction itself. Of course, there are cases where the SRC is univocal, like in the case of PH (PREPOSITION) that characterizes, in every single instance, an SWC PRE (PREPOSITION), without having any influence on the following predictions.

The interpretation of the relation Q does not seem to correspond to any commonly recognized linguistic concept. However, after what has been said on account of the SRC, we can better understand why P*, the set of all marked (in the interpretation, either “actual” or “possible”, cf. Revzin, o.c., 21) prediction structures, is mapped onto R, and not e.g. onto or into S. In fact, R is by far the smallest set of the three, and the actual frequently occurring codes are again a small subset of R. S, on the other hand, is the largest set. If we map P* onto a small set, we obtain a more general characterization; [228]doubtless an advantage at this stage in the building of the formalism. As far as the subset P* of P is concerned, we may invoke an oracle to define its establishing. But if we want to interpret the set in accordance with the general approach of the system, we take P* as the set of actually occurring prediction structures (in a given text or corpus). It should be kept in mind that this characterization of Q, when interpreted in the Kuno and Oettinger system, is in fact a simplification; I have tried to motivate this above. The question naturally arises: what is meant by “actually occurring prediction structures”? I will discuss this below in connection with the general characterization of the predictive system.

The relation G', called the “grammatical matching function” by Kuno and Oettinger, is not a function in the usual sense of the term, unless we adopt the simplification suggested above. If we decide to do so, we obtain a mapping of the set Q onto the set A. This means (since the couples of A have the “old” prediction as their first coordinate, and the SWC of the “new” word as their second): if we assume some a ∊ A*, where a is of the form (p_i, X), X symbolizing some as yet unknown s ∊ S, and given a certain p_j^* ∊ P* plus its corresponding, unique r_k ∊ R, we should have one, and only one, possible SWC for the new word. This holds e.g. in the following instance: we have an old prediction, say PD (PERIOD) and we want to continue with the new prediction “ZERO” (meaning: no new predictions are generated); now the only possible SRC of the new word is ES (END OF SENTENCE) and its SWC has to be PRD (PERIOD); the only “word” qualifying for this is, of course, the period mark (.) itself. Note that in this very simple example we have redundancy, as pointed out above; in other cases the situation will demand a more specified analysis, ie. the possibility to specify the predictions and the SWC, resp. the SCR of the preceding word (cf. discussion below).

Under this interpretation, then, it is easy to see what the relation G does: if we think of the “place” of a word X in a string as determined by its predecessor and possible successors, we have the following: given a certain predecessor structure (resulting in the old prediction) and given that we want to continue with a certain successor structure (the new prediction), there is a certain (unique) preliminary determination of the word in question by the SRC; the specified determination of its syntactic properties is then given by the SWC. In other terms, the mapping G guarantees that for a given a ∊ A*, there is some q ∊ Q, ie. a SRC and a new prediction to continue with, for some, or all, SWC of the word X (s_i ∊ S, 1 ⩽ i ⩽ m). Or, if I fix the SWC, for each s_i I have a number of r_k (r_k ∊ R, 1 ⩽ k ⩽ q), each qualified by its relevant new prediction (p^*).

Before I try out this interpretation of the formalism on some concrete example, let me make clear that my aim is not to criticize the work of Kuno and Oettinger, but rather, to clarify the issue of the word classes in their system. In this connection, the relationship between the SWC and SRC is of vital importance, but, as far as I can see, there is no ad hoc treatment of this in their work. The following then, is an attempt to supply a theoretical basis for a discussion. First then, a practical example, taken from the presentation by Kuno (1963a, 1963b).

[229]Suppose I have the old prediction SUBJECT (1X). Further, that the sequence I want to continue with after X, the word to be processed, is: DECLARATIVE CLAUSE + (and, or + NOUN CLAUSE). (+ separates individual prediction symbols, ( ) indicate possible absence, the comma alternative choices. In the notation of the grammar: SG—C + ZC—W + SG—C.) According to my first simplification, the function Q should assign a unique SRC to this prediction structure. As a matter of fact, the SRC is CO (CONJUNCTION). Now, the function G maps this couple onto an argument pair (unique, by my second simplification): (1X, CO1) (CO1 is for NOUN CONJUNCTION, only members: if, that, whether). So that the requirements on X are now quite clear: after the old prediction SUBJECT, the only three words that are compatible with the given new prediction, are if, that and whether. The case is illustrated by the example: There is nothing more uncertain than whether she is leaving or whether she is staying. (An obvious criticism: why cannot the same structure follow as an object after CO1, is countered by the use of subclassification indices on the predictions: in fact, SG—C stands for a declarative clause as a subject (—C), and so on.)

In this way, I determine the syntactic word class as a specification of the syntactic role. Now, in the concrete case, this gives some sense: CO1 is in fact one of the possible conjunctions, so that we can say: CO1 qualifies for its role, namely that of being a CO.

The example, however, was deliberately chosen a very simple one (apart from my idealization, which I will discuss later on). To get a more general idea of the relationship of SRC and SWC, one should examine the question: what SWC correspond to what SRC? The following cases should be distinguished: (1) SR determines SWC, ie. to a certain SR we have always the same SWC; (2) SR is a dummy symbol, to be determined from information contained in the topmost prediction in p_i^* (3). One SR may combine with different SWC: (a) the SR determines a category of more or less homogenous symbols; (b) the SR determines several different categories.

I will comment on each of these cases below.

1. SR determines uniquely the SWC of the word being processed.[19] There are 15 SR of this type, two (CN, SN) not being defined in the text. Most of these play a very modest role: many of them occur only in few rules, like BC (BEGINNING OF CLAUSE) in two rules with CMA (COMMA). The only big SR here is PH (PREPOSITION, 121 rules with PRE (PREPOSITION)). Together the 13 defined SR (about 40 %) occur in 259 (about 13 % of the) rules. In these cases, the simplified model would, in its interpretation, admit the dropping of the SWC altogether, since the SR determines these uniquely.

2. SR is a “dummy symbol”. The grammar has an SR, symbolized YY, that can combine with the majority of the SWC (88 out of 133). This SR occurs moreover in 536 rules (more than 25 %). However, the information that it gives us for our purpose is meagre, since the symbol YY is not a role, but an instruction. Somewhat simplified, it says: Do not assign any SR before all predictions are fulfilled, then take whatever information is contained in the topmost prediction for the word to be processed (meaning the subclassification index of this particular prediction) and transfer it to the SR. The reference of the subclassification index is to the Prediction Table: what is found there (a prediction) is made into a syntactic role. In this way, a prediction CN— (COMMA) (by means of the symbol CN—B, looked up in the subclassification index) is turned into a syntactic “role” COMPOUND OBJECT (which is not among the original SR). These “new” SR serve only to memorize a structure, not to determine it, [230]and we can therefore drop them in the present discussion. YY tells us nothing about the syntactic “value” of the place of the word to be processed, before this place has been filled up definitively.

3. The third case is split up into two, for reasons that will appear.

a) The SR determine a morphologically homogeneous class of SWC. Examples: CO (CONJUNCTION) combines only with the following SWC: CO1, CO2, CO3, CO4, CO8, CCO, XCO, YCO, CIF, all different classes of conjunctions. Likewise, GS (GERUND-SUBJECT) determines only classes of gerunds, as may be expected, AD (ADVERBS) only adverbs, and so on. At first sight this seems to fit in with our interpretation of the SR as a rough preliminary determination of the potential word-space, whereafter the more accurate determination would have to be given by the SWC of the selected argument pair. It is, however, not the case that the SR establish a partition on the set of SWC: some SWC occur in subsets pertaining to different SR, moreover some SWC do not occur in their appropriate subsets at all (like CO5, CO7 that do not pertain to the SR CONJUNCTION). Moreover, it can be asked what relevance the criterion of morphological similarity has to the present issue, and how we define similarity in morphological terms. Rather than discuss these matters here, however, let us now consider the second group of SR.

b) In this group, one finds 6 SRC (representing altogether 334 rules) that determine morphologically heterogeneous groups of SWC. As an instance, I will discuss the biggest group: SV (SUBJECT OF PREDICATIVE VERB, 24 SWC, 139 rules). In this group one finds, besides the expected nominal (pronominal, relative, numerical) SWC: a number of adverbial classes (comprising such adverbs as very, too), adjectival classes, conjunctions, participles (but no infinitives). The difficulty of giving a reasonable interpretation of, say, an adverb like too playing the syntactic role of SV, together with the problems encountered above in subgroup 3a, warns against dismissal of these difficulties as hardships due only to an incomplete interpretation of the concept of SR in a minority of cases (besides, the SR of this group form rather a strong minority, occurring in 16 % of the rules).

How then, can one assign an SR SUBJECT OF PREDICATE VERB to an adverb? If we look up the appropriate rules in the Grammar Table, we will find (in this case as in the other dubious roles) that the role is assigned not to the word in question only, but to the virtual group that is constituted by the word itself and some (or all) of the words that belong to the prediction that follows. In our example (SE, AV8) we have Too initiating a group: Too many people, which is the subject of came in the structure (prediction) Too many people came. The SR thus assigns a structure of higher level (in this context: higher constituent level) to the word in question, and why do we need SR for this? Apparently because the qualification by prediction alone is not sufficient: why not take too many people as a prediction fulfilling the expectation of an object, e.g.? In this case I would have to assign a different SR to the adverb. If this be correct, there are two consequences: (1) the SR does not necessarily concern the constituent immediately above (in the tree representation) the word to be processed; (2) the SR does not even necessarily concern a constituent of the sentence: it may concern a virtual prediction that is never realized. (See for discussion of this point, Kuno 1963b, I-104)[20] If we admit this interpretation of the SR, it follows that [231]my first simplification above (the relation Q) does not hold. Predictions (especially the shorter ones) can map into different SR. A way out (if one wishes to preserve the formal claim of uniqueness) would be to differentiate the predictions (so that an object prediction is different in its symbolism from a subject prediction). In fact, this is done by Kuno and Oettinger, as I have shown above, but for other reasons, not in order to preserve a unique mapping. Moreover, the idea behind the model was to find out what relevance the SR has for the “word-place” (position) to be examined. It now turns out that in a great many cases the SR cannot be said to harmonize with the SWC concept at all, because the former concerns (possible) structures (in my sense), whereas the latter concerns single words. In the other cases, the information about SWC provided by SR is either trivial (case 1) or irrelevant (case 2) or finally equivocal (case 3a).

The other reason why the formalism sketched above does not admit of a concrete interpretation in the sense of Kuno and Oettinger lies in the fact that the relation G' is not unique either. Let us take a concrete example.

We have the “old” prediction SE (SENTENCE). The new prediction consists of the sequence: ATTRIBUTIVE ADJECTIVE + MODIFIED SUBJECT + COMMA + SENTENCE (possible examples: many people coming, the conference was a great success, or: intelligent people existing, we must compete with them). We take SP (SUBJECT OF PREDICATE VERB) as our SR. The obvious interpretation is that the word X must fit into a group that is already a subject (many people, intelligent people). According to the Grammar Table (p. 170—1) there are two possibilities: either the word X belongs to the class AV6 (more) or it belongs to AV8 (too). So we have the argument pairs (SE, AV6, and SE, AV8): there is no unique mapping from Q to A. Of course one could discuss the reasons for establishing two different classes of adverbs, of which the one only contais more (on account of a possible than following) and other only too (because of possible discontinuity, cf. Kuno 1963b, I-30), but this is not the point at issue. The point is that we cannot use the SR for distinguishing between the two occurrences, if, at any rate, we want to confine ourselves to the currently recognized SR (note that the mapping Q in fact is unique in this particular case). Supposing, therefore, that we have a certain new prediction, that has to play the role (whole or in part) of a subject, we still have the problem how to distinguish two different structures (admitting the usefulness of the distinction between the two examples quoted above). The burden of this distinction lies entirely upon the SWC: once we want to distinguish, we have to do it by means of the SWC, since there are no other means available (with the exception of those noted above).

Looking at the problem from a slightly different angle, we could say: the SWC establish a partition (at best) of the set of words, the SR establish a set of subsets on the set of possible phrases of the language. These phrases can consist of words, and if such a word with a unique SR happens to be the only member of its class in the SWC partition, we have, of course, redundancy (case 1 above): the SR gives us the SWC, trivially. In all other cases, the SR is not sufficient to establish (together with the new prediction) a set in the SWC partition that will pick the right argument pair in A, and in some cases (3b above) this interpretation of the SR is directly contradicted by the facts.

Discussion. Above, I have tried to define the relationship between SWC and SR by means of a formalism containing two binary functions. It turns out [232]that the interpretation of the formalism in terms of Predictive Analysis according to Kuno and Oettinger hurts the facts in several points. To be discussed now, is the question: what happens if we replace the two functions Q and G by general mappings (non-unique relations)?

Before entering into the discussion I would like to sum up the following observations:

1. The grammar contains both SWC and SR. There seems to be no reason to consider one of these as superfluous.[21]

2. The difference between the SWC and SR is one of levels (in the present system, levels of constituents, but equally possible would be an interpretation in other terms).

3. The SR associated with the new prediction is not the SR of the prediction itself, but of the word that is prospectively heading the new prediction. The SR of the prediction itself, if expressed, can be inferred from the suffixed indices of its symbols (like —C for SUBJECT etc.).

4. Since the word that is to appear in front of the new prediction may actually form a structure with (part of) the new prediction, the SR associated to the prediction may contain the claim that the SWC of the corresponding word be compatible with the SR specified in the couple q. As we have seen above, this claim is a very weak one, especially in the case of longer predictions, where structures of more and more differentiated character may appear.

5. The cases where the SR determines a SWC uniquely are in fact trivial, as we have seen above. In all other cases, the distinction on possible structures has still to be performed after the SR has been chosen.

I will now discuss the relations Q and G. What happens if we decide to replace the unique mapping by a general mapping? In both cases, the question is: how to characterize the subsets of the Cartesian products without having recourse to unique functions?

In the case of Q, the Cartesian product is P* × R. The couples that qualify for the relation Q are those where an SR of the processed word harmonizes with the SR of the allowed prediction. If we leave the predictions in a general form, ie. without indices for subclassification, it is to be expected that some predictions map into different syntactic roles (like SUBJECT or OBJECT, if the prediction is, f.ex., a DECLARATIVE CLAUSE). But, as we have seen, in most cases the predictions are specified so as to qualify for the mapping Q (while in the case of the “syntactic role” YY they specify the SR subsequently). Besides, about half of the total number of SR specify a unique SWC, so in this case the problem of uniqueness is carried over to the relation G. Because of the low frequency of occurrence of a relatively great number of SR (16 out of 34 occur in altogether 54 out of about 2100 rules), the danger of [233]non-uniqueness is still further reduced. I think that the intensional criterion of harmonizing with the prediction that follows is not too badly represented by the extension of the relation Q, if defined in my sense, but of course it has never been a theoretical claim in ASA.

The relation G. Here it should be kept in mind that the relation G', as defined by Kuno and Oettinger, is mainly empirical. The question how to determine which argument pairs map into which couples (p^*, r) is settled by a procedure that answers the question: What structures (ie. sequences of words) can follow, given 1. the old prediction, 2. the SWC of the word to be processed? The boundaries of the possible answers are given by the corpus of text I want to analyze (plus whatever I think might occur in a similar kind of text, see Kuno 1963a, II-3) and, to a certain extent, by the length of the individual structures (usually one recognizes no structures that exceed normal sentence length). The determination of the relation G' is thus paramount in establishing the intension of the “syntactic word”; the question to be answered is the following: what consequences has the dropping of the uniqueness claim on G for the concept of SWC? The answer to this question is from the negative: under the given interpretation of the formalism, it is not the case that the SR determines the SWC in a preliminary way (as one remembers, this was the conclusion we arrived at in the “idealized” interpretation). That in many cases the SR in fact determine (uniquely or just anticipatorily) the SWC is either trivial or incidental, and does not follow from the definition of the relation G.

The immediate consequence of this answer is that we have so to speak absolute freedom in setting up SWC: indeed, there is no reason why we should not split up any word class in subclasses to account for some special possible prediction. And, of course, as a practical means of establishing a subset of couples [P_i, S_j), G' (P_i, S_j)], called grammar rules, there is nothing to be said against it. The question to be raised is rather: will not the freedom of choice for the subclassification of the SWC, making “the word class distinction explicity carry the burden of representing different structures” (Kuno 1963b, I-9), be detrimental to the concept of word-class itself? Indeed, when looking at the Word-class Table in Kuno and Oettingerʼs grammar, one cannot help feeling that there is a great amount of ad hoc classification (of course this is no argument in itself against any classification, as long as one keeps in mind what the hoc is). In a predictive analysis like the one discussed here, the word-classes have to account for all possible structures that may follow the word they subsume; the analyzer proceeds from word to word, not from structure to structure. What we do in assigning word-classes in ASA is, in fact, incorporating a distinction between structures (sequences of elements, not necessarily or only words) into single words. Is there any point in aiming at uniqueness for the relation G? First, let us consider uniqueness from A to Q (for every a, a unique q, or: G (A) = Q). Obviously, there is no point in defining a unique q for every a: this would not only be impractical (endless duplication of rules), but impossible (since evidently some argument pairs do have different prediction possibilities). What is meant by Kuno is rather that every a maps onto a unique set of predictions (or more precisely, ele[234]ments of Q): at least, this is how I have tried to interpret uniqueness with respect to his relation G'. Intuitively speaking, uniqueness here means that we have to know what predictions we can make every time a given argument pair appears. As explained above, the syntactic role of the word “in the machine” does not play a decisive part in assigning possible following structures, and the whole burden of choosing the right alternatives (after a certain “old” prediction) rests on the SWC of the argument pair.

As to uniqueness from Q to A [G (Q) = A], I have discussed the advantages of this conception above. The question remains: is it practical, and how can we achieve it? As to the first part of the question, I will not venture any answer. The second part will be answered only tentatively. My suggestion is the following: after establishing uniqueness for Q (we have seen that this should not cause too much difficulty) one will already have couples q where the predictions are specified with regard to the syntactic role of the word that is to precede them. Uniqueness from Q to A can be obtained either by ulterior specification of the new predictions (keeping the old prediction constant), or by reducing the number of word-classes.

Example: the couple q above that maps into two different argument pairs [(SE, AV6 and (SE, AV8)], can be split up into two different qʼs (so to say, incorporating the word-class division into the prediction: one p^* if too precedes, another p^* if the preceding word is more). This seems to be a clumsy way out of the difficulties and it would certainly lead to an enormous augmentation of the possible predictions, on grounds that are not structurally relevant for the predictions themselves.

On the other hand, reducing the two AV classes to one would deprive us from the desired distinction between the two types of adverbs (taking for granted that it is a desired, and structural, distinction).

There seems, however, to be another possibility: why not differentiate the qʼs on the syntactic roles? The main obstacle here is that the SR coordinate of the couple (p^*, r) is the syntactic role played by a word class of a subrule (cf. Kuno 1963b, II-32 and passim), whereas the SR often (at least in the interesting cases) concern a structure, not a single word. It would seem more natural to associate with each structure one (or more, if one does not insist on uniqueness of this mapping) syntactical role(s); this SR is then the role played by the structure itself, ie. by the prediction or part of it, not by the (word)-class of the word that comes before the structure. As shown above, this is in fact the only possible interpretation of some SR (like INSERTION for COMMA: it is not the comma that is an insertion, or plays the part of an insertion, but rather what follows the comma); so what we do here, is only to make explicit, and generalize, a conception that is already latent in the work of Kuno. We will still need word-classes, and a great many of them, since the analyzing approach is word-by-word, from left to right; but we will have no interference from the SR on the word level, which is in accordance with the general conception of SR as belonging to a higher level of description (not necessarily constituent structure, like in the present grammar). We will still predict structures, but they will be syntactically rather than lexico-syntactically different; an immediate consequence of this is that the structures under this new conception are smaller units that may „generate“ new struc[235]tural units in the case of a fulfilled prediction.[22] The only question to be answered will then be if the prediction thus characterized (the q) can subsume the syntactical word-class of the word that precedes to form a new structure. The task of differentiating the structures would then be placed on the SR, not on the SWC; the natural consequence would be that only such syntactical word-classes would have to be recognized that were parts (constituents, under the present system) of structures, which I think is an advantage from the viewpoint of overall grammatical description (but perhaps uninteresting from that of ASA). G would then be defined as the function that assigns a unique argument pair to every specified prediction. The main drawback of this conception is that we may have to make several passes through the sentence in order to be sure that we have subsumed constituents not only under their immediate, but under their mediate constituents as well.

 

R É S U M É

Slovní druhy v automatické syntaktické analýze

Tradiční gramatika rozlišuje základní pojmy slovních druhů a syntaktických funkcí. V novějších pracích na strojovém překladu a automatické analýze jazyka získaly tyto pojmy novou aktuálnost a potřeba jejich přesnějšího vymezení se stala naléhavější. Tato stať je věnována otázkám uvedených pojmů v souvislosti s automatickou syntaktickou analýzou v té podobě, jak byla formulována v prediktivní gramatice S. Kuna a A. G. Oettingera. Pracuje se s formálním aparátem, který je určitým upřesněním Kunovy „grammatical matching function“. Porovnáním určitých podmínek daných tímto formálním aparátem s možnými interpretacemi autor dospívá k tomuto závěru: pojmy syntaktických slovních druhů a syntaktických funkcí mají být přiřazeny k různým úrovním popisu, takže každá jednotka, která je v analýze charakterizována, má být zachycena co do syntaktického slovního druhu i co do syntaktické funkce. — Čistě formální charakteristika těchto pojmů může být podána jen za cenu značné idealizace jazyka; není však na místě považovat je jen za praktickou pomůcku pro analýzu, popř. pro strojový překlad. Potřeba formálnějších charakteristik a přísnějších vymezení je demonstrována na příkladech vzatých z práce Kunovy; následuje rozbor předběžných výsledků. Zůstává pak alternativa — buď zvolit formální popis nevhodný pro praktické účely, nebo praktický, použitelný systém (jako je Kunův), který má určité nedostatky z hlediska teoretického.

Slovo a slovesnost, ročník 27 (1966), číslo 3, s. 220-235

Předchozí Josef Vachek: Československé kolokvium o otázkách fonologie a fonetiky

Následující Lubomír Doležel: Ještě k jednomu modelu jazykového kódování