O jedné formalizaci větného rozboru

Ladislav Nebeský

[Články]

(pdf)

Об одной формализации анализа предложения / Au sujet d’une formalisation de l’analyse des phrases

Matematické metody v lingvistice těží ze čtyř zdrojů: matematické statistiky, teorie informace, teorie množin a matematické logiky. Aplikace posledních dvou disciplín spolu těsně souvisí, obě vedou ke konstrukci různých matematických modelů jazyka, přesněji matematických modelů různých lingvistických pojmů. Většinou jde o formalizaci lingvistických pojmů již dříve známých. Tato formalizace není samoúčelná. Je nutná pro strojový překlad, automatickou gramatiku, informační jazyk, automatické referování a jiné problémy aplikované lingvistiky, ale má také význam pro lingvistiku teoretickou. Účelem matematického modelu je z minima platných faktů (axiómů, které nedokazujeme) a pravidel deduktivně vyvodit maximální počet lingvistických pojmů. Nové metody přinášejí také nové výsledky.[1]

Tento článek je pokusem o formalizaci jednoho postupu větného rozboru. Základní matematický pojem, o nějž se budeme opírat, je pojem orientovaného grafu.[2] Mějme dánu jakoukoli neprázdnou množinu U; její prvky nazveme uzly. Předpokládejme, že mezi některými uspořádanými dvojicemi uzlů je dán jakýkoli pevně stanovený vztah; tyto dvojice budeme nazývat hranami. Množinu hran označíme H. Množinu U společně s množinou H nazveme orientovaným grafem. Je-li množina uzlů konečná, mluvíme o konečném orientovaném grafu (dále [105]stručně jen graf). Termín graf (stejně jako terminologie teorie grafů vůbec) vznikl z této názorné reprezentace: Každému uzlu přiřaďme nějaký bod roviny, a jestliže uspořádaná dvojice uzlů tvoří hranu, veďme od prvního vrcholu dvojice k druhého šipku.

Tak např. graf s uzly A, B, C, D, E, F a hranami [A, B], [B, C], [C, B], [A, D], [E, E] lze kreslit mimo jiné těmito způsoby:

 

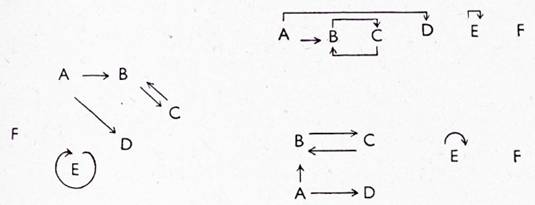
Matematický pojem grafu je abstrakcí ze všech takových kreseb.

Větný rozbor vždy spočívá v tom, že podle daných kritérií hledáme ve studované větě nějaké vztahy. Dosti často jde o vztahy mezi uspořádanými dvojicemi větných členů. Pomůckou větného rozboru bývá konstrukce obrázku, kterému se někdy říká graf (i když mnohdy grafem v matematické terminologii není). S něčím takovým se setkáváme např. v Novočeské skladbě V. Šmilauera (Praha 1947). Jeho nákresy připomínají graf věty, jehož uzly tvoří její větné členy, i když jsou kresleny podle jiných pravidel. Jeho pojem nákresu je však bohatší než pojem grafu, neboť respektuje pořadí slov ve větě.

V tomto článku budeme definovat graf, který popisuje podobný způsob větného rozboru. Ke každé větě budeme konstruovat orientovaný graf, jehož uzly budou větné členy. To znamená, že v množině uspořádaných dvojic větných členů studované věty budeme určovat jistou binární relaci. Hrana bude směřovat od větného členu x k větnému členu y (x bude v relaci s y) právě tehdy, má-li y „bezprostředně perifernější postavení“ než x. Co rozumíme „bezprostředně perifernějším postavením“ — čili podle jakých pravidel graf ve větě konstruovat —, budeme definovat pomocí formálního aparátu.

Při definování nějakého pojmu musíme vycházet z jiných pojmů, které považujeme za výchozí. Výchozí pojmy se uvnitř studovaného systému nedefinují; předpokládá se, že jsou vzhledem k němu předem dány. Pro nás budou výchozími pojmy věta (resp. množina všech vět), význam věty a jistá binární relace na množině významů, jejíž funkci později vysvětlíme. Než přistoupíme k definicím základních pojmů, dohodněme se, že pod termínem slovo budeme rozumět výskyt větného členu ve větě.

Mějme nějakou neprázdnou konečnou množinu slov L. Textem nazveme každou konečnou posloupnost slov L. (To znamená, že textem nebudeme rozumět pouze seřazení slov podle určitých pravidel, nýbrž zcela libovolné uspořádání kterýchkoli slov z L bez ohledu na to, dává-li tato posloupnost slov smysl či nikoli.) Množinu všech textů označíme písmenem T. Budiž A ε T, x ε L (symbol ε značí nále[106]žení prvku do množiny). Jako x E A budeme zkráceně psát výrok „slovo x je členem posloupnosti slov (textu) A“. (Symbol E tedy značí něco poněkud jiného než než symbol ε.) Mějme texty A a B. Jestliže text B je roven textu A nebo jej z textu A dostaneme vypuštěním několika nebo všech slov, řekněme, že B je textem vybraným z textu A, což označíme B  A.

Nechť je dána nějaká neprázdná množina S, kterou nazveme množinou významů. Na této množině nechť je definována binární tranzitivní a reflexívní relace, kterou označíme . Dále mějme dánu množinu V, která je podmnožinou množiny T. Texty, které jsou prvky množiny V, nazveme věty. Nakonec budiž dáno zobrazení φ, které každé větě z V přiřazuje nějaký význam (ale jediný, věty s více významy nebereme v úvahu) z S. φ je tedy zobrazení V do S. Je-li A ε V, označíme jako φ A význam věty A.

Je pochopitelné, že z formálního hlediska lze V, S a φ volit různě v mezích, v kterých jsou splněny předpoklady na ně kladené. Ne každé interpretace splňující formální předpoklady můžeme v lingvistice využít. Ukázkou interpretace, která je lingvisticky významná, je např. následující interpretace.

Množinou V budeme rozumět množinu všech vět nějakého jazyka, kterým lze přiřadit právě jeden význam. Je-li A ε V, B ε V, potom φ A  φ B bude platit právě tehdy, existuje-li způsob, jakým lze význam φ B zkonstruovat na základě významu φ A, čili je-li význam φ A primitivnější než φ B. Označme jako A₁, A₂, A₃ tyto věty Prší, Hustě prší, Není pravda, že prší. Vidíme, že význam věty A₂ je konstruován na základě významu věty A₁. Stejně i význam věty A₃ je konstruován na základě významu věty A₁, i když znamená jeho popření. (Ale právě z toho, že jej popírá, vyplývá, že je budován na jeho základě.) Tedy platí φ A₁  φ A₂, φ A₁  φ A₃.

Nyní se vrátíme k formálním úvahám a přistoupíme k důležité definici. Je-li A ε V, B ε V, řekneme, že věta B je podvětou věty A, když zároveň platí výroky B  A a φ B  φ A.

Smysl této definice v naší interpretaci si osvětlíme na následujícím příkladě. Vezměme tuto větu (A*): Hladina některých přítoků této velké řeky klesá k normálu. Vidíme, že věta Hladina některých přítoků klesá je podvětou věty A*, zatímco věta Hladina velké řeky klesá podvětou věty A* není.

Konstrukci grafu reprezentujícího větný rozbor provedeme na základě binární relace mezi slovy každé věty A ε V.

Předpokládejme, že A ε V, x E A, y E A, x ≠ y a že pro každou podvětu C věty A platí tvrzení y E C ⇒ x E C a pro žádné z E A, z ≠ x, z ≠ y neplatí současně y E C ⇒ z E C a z E C ⇒ x E C, pak řekneme, že ve větě A leží slovo y bezprostředně periferněji než slovo x — označíme x → y. Vidíme, že z této definice neplyne, že by nemohlo současně platit x → y a y → x; zároveň vidíme, že relace → je antireflexní a antitranzitivní.

Je zřejmé, že každé větě A přiřazuje relace → graf.

Graf věty A* vypadá v naší interpretaci takto:

             hladina     ← klesá   →   k normálu

                 ↓

             přítoků       → některých

                 ↓

     této ← řeky        → velké

 

[107]Na závěr se stručně zmíníme o některých otázkách, které takto definovaný větný rozbor přináší.

1. Z grafu věty A* vidíme, že šipka směřuje jen od predikátu k subjektu, protože věty typu „klesá“ jsou v češtině na stejné úrovni jako „ona klesá“, kdežto větám typu „hladina“, bereme-li je samy o sobě bez situace nebo kontextu, nelze přiřadit význam jako větám.

2. V grafu věty A* směřuje šipka od predikátu k předložkovému pádu, a ne již naopak. Vezmeme-li však větu Starý Horýnek lnul k podniku (V. Šmilauer, op. cit., 225), dostáváme tento graf:

Starý ← Horýnek ← lnul ⇄ k podniku.

Zde jsou predikát a předložkový pád „na stejném stupni perifernosti“. Tato nejednotnost vyplývá z toho, že „u předložkových pádů pozorujeme zvlášť patrné stálé přecházení od platnosti příslovečné k platnosti předmětné. Jakmile nastane těsné spojení mezi slovesem a pádem, stává se pád předmětem“ (tamtéž, 224).

3. Jakousi anomálii budou v našem formálním systému tvořit ty věty, kde je subjekt (1. nebo 2. osoba) vyjádřen jen slovesnou koncovkou.

4. Další nesrovnalostí je postavení příklonek. Při hledání podvět by vlivem postavení příklonek docházelo k nesrovnalostem. Na dané úrovni však k této anomálii nepřihlížíme.

Na konec zdůrazňujeme ještě toto: Je pochopitelně prakticky nemožné mít dánu množinu všech vět (tedy množinu V) ve formě jejich seznamu. Stejně tak je ve skutečnosti nemožné mít dánu nějakou množinu významů S, do níž lze tento seznam vět zobrazit. To však není zapotřebí. Pro aplikaci našeho formálního principu stačí, máme-li jednoznačné kritérium pro to, abychom o každém textu, s nímž se můžeme za daných okolností setkat, uměli rozhodnout, je-li větou, a abychom pro každé dvě věty poznali, jsou-li jejich významy ve vztahu, který jsme popsali.

 

R é s u m é

ОБ ОДНОЙ ФОРМАЛИЗАЦИИ АНАЛИЗА ПРЕДЛОЖЕНИЯ

С формальной точки зрения анализ предложения часто основан на построении какого-то графа (в смысле математической теории графов). Обыкновенно узлам графа присоединяем члены предложения и ребра графа потом отображают отношения между членами предложения.

В этой статье определяется прием, который позволяет каждому предложению присоединить такой граф. Описанный нами метод основан на следующих основных понятиях: на множестве всех предложений, на множестве значений, в котором множество предложений отображается, и на определенной бинарной реляции между значениями.

Slovo a slovesnost, ročník 23 (1962), číslo 2, s. 104-107

Předchozí Eleonora Slavíčková: Metoda morfémové analýzy založená na aplikaci teorie pravděpodobnosti

Následující Jaromír Bělič, Bohuslav Havránek, Alois Jedlička: Problematika obecné češtiny a jejího poměru k jazyku spisovnému