Některé otázky závislostní koncepce syntaxe

Ladislav Nebeský

[Články]

(pdf)

Некоторые проблемы зависимостей концепции синтаксиса / Quelques questions concernant une conception de dépendance de la syntaxe

V tomto článku si všimneme závislostní koncepce syntaxe, jak se může jevit z hlediska teorie grafů,[1] přistoupíme-li ovšem na stanovisko, že tato teorie umožňuje formalizaci alespoň některých podstatných rysů syntaxe. Matematické modely jazykových jevů, tj. formální systémy lingvisticky interpretovatelné, mají ovšem i vlastnosti, které lze nalézt teprve matematickými prostředky. Na obsahové úrovni jsou totiž nezřetelné, a proto jejich studium nemůže být lingvisty předem požadováno. Domnívám se, že v objevování a studiu především těchto vlastností modelů jazyka je smysl aplikace matematiky v lingvistice. Vede-li cesta od lingvistických jevů k matematickým strukturám, lze na základě jejich studia klást nové otázky mířící zpět k lingvistice. Pět takových otázek zde bude položeno.

 

1. Z formálního hlediska lze popis větné struktury v závislostní koncepci založit na nalezení orientovaného grafu, jehož uzly jsou výskyty slovních tvarů ve větě (různé výskyty téhož tvaru jsou tedy různými uzly) a v němž je uspořádaná dvojice uzlů hranou, právě když druhý z obou uzlů závisí na prvém.[2] Zpravidla se předpokládá, že orientované grafy popisující závislostní strukturu vět jsou vrcholové stromy; tohoto předpokladu se zde přidržíme.[3] Vrcholový strom je pojem značně širokého použití. Setkáváme se s ním obvykle tam, kde jde o nějakou hierarchizaci. Zavádí se různými způsoby: jako již zmíněný případ orientovaného grafu, částečného uspořádání, polosvazu, zobrazení nebo konečně jako obohacení jednoho typu neorientovaných grafů-stromů. V souvislosti s lingvistickými aplikacemi bývá běžný první způsob, pro nás však bude naopak zajímavý způsob poslední[4].

Konečnou množinu U spolu s množinou H jejích některých dvouprvkových podmnožin nazveme stromem, právě když ke každé uspořádané dvojici p, q prvků z množiny U existuje právě jediné celé nezáporné číslo n a právě jediná posloupnost r₀, …, r_n navzájem různých prvků z U taková, že r₀ = p, r_n = q a je-li n > 0, tak {r₀, r₁}, …, {r_n—1, r_n) jsou prvky množiny H. Uvedený strom označíme jako (U, H); přitom prvky množiny U(H) nazveme jeho uzly (hranami). Uvedenou posloupnost nazveme cestou z uzlu p do uzlu q; číslo n nazveme její délkou; o každém z uzlů r₀, r₁, …, r_n řekneme, že na této cestě leží. Jako příklad uvažujme strom (U₀, H₀) s uzly b, d, k, m, o, p, s, t a hranami {t, b}, {b, p}, {p, s}, {s, o), {m, k}, {k, o} {o, d}. Posloupnost p, s, o, d je zřejmě cestou z uzlu p do uzlu q; její délka je rovna třem. (Lingvistickou interpretaci a geometrické znázornění stromu (U₀, H₀) viz níže.)

O stromu tedy platí, že ke každým dvěma jeho uzlům existuje právě jediná cesta jdoucí z prvního z nich do druhého. Stromy jsou speciálním případem konečných neorientovaných grafů: jsou to právě ty z nich, jejichž každé dva uzly lze (v obou směrech) spojit jedinou cestou.[5] [21]Z jejich základních vlastností uveďme alespoň to, že počet hran každého stromu je o jednotku menší než počet jeho uzlů.

Je-li (U, H) strom a r nějaký jeho uzel, budeme uspořádanou trojici (U, H, r) nazývat vrcholovým stromem (vrcholem je uzel r). Prvky množiny U(H) budeme považovat za uzly (hrany) vrcholového stromu (U, H, r). Je-li {p, q} nějaká jeho hrana, potom se délka cesty z uzlu r do uzlu p o jednotku liší od délky cesty z uzlu r do uzlu q. Tento jednoduchý fakt nám dovoluje převést právě zavedený pojem vrcholového stromu do podoby orientovaného grafu: každou hranu budeme orientovat ve směru k uzlu vzdálenějšímu od vrcholu.[6] Příkladem vrcholového stromu je (U₀, H₀, s).

Všimněme si této české věty:

(1) Přítel tvého bratra slíbil odvézt můj kufr domů.

Označíme-li vrchol (tj. řídicí uzel) antikvou a znázorníme-li hrany lomenými čarami, lze větě (1) přiřadit tento vrcholový strom:[7]

 

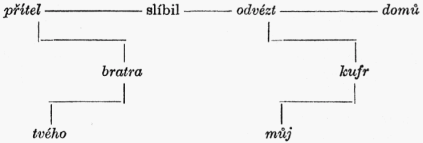
Protože se ve větě (1) žádný slovní tvar nevyskytuje více než jednou, lze uzly uvedeného grafu přímo ztotožnit se slovními tvary. Všimněme si, že kdybychom každý slovní tvar nahradili jeho počátečním písmenem, dostali bychom vrcholový strom (U₀, H₀, s).

Stojí za zaznamenání, že volba vrcholu pojem stromu v jistém smyslu příliš neobohacuje: z daných n uzlů lze sestrojit n^n—2 různých stromů; avšak počet různých stromů s vrcholem je pouze n-násobkem tohoto exponenciálně rostoucího čísla. Ovšem každý strom má jakési své „přirozené vrcholy“, především střed a těžiště (jak střed, tak i těžiště může tvořit buď jeden uzel, nebo dvojice uzlů spojených hranou); tyto pojmy lze dále zobecnit připuštěním různé „váhy“ jednotlivých uzlů, či různé „délky“ hran.[8] Strom věty (1) má jediný střed i jediné těžiště, obojí totožné s vrcholem (tj. tvarem slíbil).

Považujeme-li strom za vhodný základ popisu větné struktury, je smysluplné formulovat následující otázku: Lze nějak globálně charakterizovat věty, v jejichž stromu je vrchol blízko středu (těžiště), v opozici k těm větám, v jejichž stromu je vrchol od středu (těžiště) podstatně vzdálen?[9]

 

2. Studium (vrcholových) stromů má v matematice již dlouhou tradici. Poměrně nové je však vyšetřování (vrcholových) stromů, jejichž množina uzlů je uspořádána v závislosti na vlastnostech (vrcholového) stromu, což je téma, které vzniká konfrontací závislostní struktury věty a jejího slovosledu. Jak známo, slovosledně [22]uspořádané vrcholové stromy vět splňují většinou podmínku projektivity, kterou lze formulovat následujícím způsobem.

Je-li (U, H, r) vrcholový strom s uspořádáním uzlů <, řekneme, že je projektivní, když pro jeho libovolné tři uzly u, v, w takové, že min (u, w) < v < max (u, w), platí:[10] leží-li uzel u na cestě z vrcholu r do uzlu w, leží také na cestě z vrcholu r do uzlu v.[11]

O větě budeme říkat, že je projektivní, je-li projektivní její slovosledně uspořádaný vrcholový strom. Snadno se lze přesvědčit, že věta (1) je projektivní; neprojektivní věty často snadno poznáme podle neobvyklosti jejich slovosledu (srov. např. Vánoční nadešel čas).[12] Vzhledem k tomu, že jsme vrcholový strom zavedli jako strom, v němž je navíc zvolen některý jeho uzel za vrchol, je nasnadě otázka, nakolik je projektivita závislá na volbě vrcholu, tj. zda ji lze rozštěpit na dvě nezávislé vlastnosti, z nichž jedna je na volbě vrcholu nezávislá. Ukážeme, že to možné je.

Je-li (U, H) strom s uspořádáním uzlů <, řekneme, že je hladký, právě když pro jeho libovolné dvě hrany {p, q} a {u, v} platí: je-li p < u < q, je v ≦ q (viz o. c. v pozn. 9). To tedy znamená, že strom je hladký, právě když neobsahuje žádnou dvojici hran {r, s} a {x, y}, takovou, že platí r < x < s < y, jak je tomu např. v stromu

 

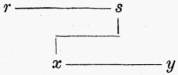
Snadno nahlédneme, že každý strom o nejvýše třech uzlech je hladký.

Platí následující tvrzení: Vrcholový strom (U, H, r) s uspořádáním < je projektivní tehdy a jen tehdy, když strom (U, H) s uspořádáním < je hladký a současně uzel r leží na cestě z minimálního do maximálního uzlu (v uspořádání <).[13] Tato druhá podmínka je značně jednoduchá; v jistém smyslu se týká jen tří uzlů (ty ovšem nemusí být různé). O větě budeme říkat, že je hladká, je-li hladký její slovosledně uspořádaný strom. Rozštěpení projektivity na dvě navzájem nezávislé vlastnosti nám dává možnost třídit neprojektivní věty do tří disjunktních kategorií: na ty, které jsou hladké (Vánoční nadešel čas), na ty, které nejsou hladké, ale splňují druhou podmínku (Má plný sklad zásob), a konečně na ty, které nesplňují ani jednu z obou podmínek (jejich slovosled bývá značně neobvyklý, jako např. ve větě Mít chtěl plný sklad zásob).

Všimněme si, že ke každé větě, která není projektivní, ale přitom je hladká, lze formulovat jinou větu, která se od původní liší jen přidáním dalšího slovního tvaru (který je závislý přímo na řídicím uzlu, tj. vrcholu) a která již není hladká. V této souvislosti se nabízí další otázka, jejíž platnost lze ovšem ověřit jen empiricky: Je pravda, že nepříliš krátké neprojektivní věty, s nimiž se lze v textech setkat, nejsou obvykle ani hladké?

 

3. Je-li (U, H) strom s uspořádanými uzly, budeme té cestě, která začíná v minimálním a končí v maximálním uzlu, říkat hlavní cesta. Je-li (U, H, r) nějaký [23]vrcholový strom s uspořádanými uzly, je projektivní, právě když (U, H) s týmž uspořádáním je hladký a když uzel r leží na hlavní cestě.

Hlavní cesta zaujímá v stromu s uspořádanými uzly výjimečné postavení. Zvolíme-li na ní některý uzel za vrchol a shledáme-li, že takto vzniklý vrcholový strom je projektivní, je projektivním vrcholový strom s kterýmkoli uzlem ležícím na hlavní cestě jako s vrcholem. Při srovnávání hladkosti a projektivity jsou si vlastně všechny uzly na hlavní cestě z funkčního hlediska rovny. Hlavní cesta v hladkém stromu je dále zajímavá tím, že na ní uzly následují tak, jak jsou uspořádány (tuto vlastnost mohou mít i jiné cesty hladkých stromů, nikoli ovšem nutně všechny, o. c. v pozn. 9). Tak např. hlavní cesta stromu věty (1) je:

přítel —— slíbil —— odvézt —— domů.

To, že většina vět je projektivních, lze říci i jinak: většina vět je hladkých a řídicí slovo je uzlem hlavní cesty. Často však také holý podmět bývá uzlem hlavní cesty. Zdá se, že hlavní cesta není zdaleka zajímavá pouze z formálního hlediska a že by bylo smysluplné zkoumat, jak a v jakých vzájemných souvislostech je hlavní cesta věty vytvářena z větných členů. Je pravda, že hlavní cesta věty bývá pro její stavbu významná v tom smyslu, že je jí věta v nějakém svém podstatném rysu charakterizována spíše než kteroukoli jinou stejně dlouhou cestou?

 

4. Tvrzením, které jsme uvedli v části 2, se vztah projektivity a hladkosti nevyčerpává. Lze dokázat, že pojem projektivního vrcholového stromu s uspořádanými uzly je ekvivalentní pojmu danému dvojicí hladkých stromů s uspořádanými uzly, v níž uzly prvního stromu až na maximální uzel předcházejí uzly druhého; maximální uzel prvního stromu je totožný s minimálním uzlem druhého hladkého stromu. Studium projektivních vrcholových stromů lze tedy nahradit studiem dvojic takto vzájemně svázaných hladkých stromů.[14]

Uvedený výsledek vede k dělení vět do dvou částí, levé a pravé. Levou (pravou) část věty tvoří všechny výskyty slovních tvarů ležících nalevo (napravo) od řídícího tvaru společně s ním. To znamená, že levou částí věty (1) je řetěz přítel tvého bratra slíbil a její pravou částí řetěz slíbil odvézt můj kufr domů.

Zacházíme-li s oběma částmi nějaké věty stejně jako s větami, je zřejmé, že uvažovaná věta je projektivní, právě když obě její části jsou hladké. (Přitom obě části české věty jsou zpravidla opět českými větami a jejich vrchol je shodný s vrcholem věty původní.) Rozdělení vět do zmíněných dvou částí není ovšem identifikovatelné s dělením věty na bezprostřední složky. Tím se dostáváme k další otázce: Jak lingvisticky charakterizovat levou a pravou část věty?

 

5. Uvažujme opět strom (U, H) s uspořádáním uzlů <. Je-li u kterýkoli jeho uzel, který je různý od minimálního uzlu v uspořádání <, označíme jako l(u) maximální uzel ze všech uzlů v takových, že v < u a že existuje uzel w tak, že u ≦ w a {v, w} je hrana. Podobně je-li u různý od maximálního uzlu, označíme jako p(u) minimální uzel ze všech takových uzlů v, že u < v a že existuje uzel w tak, že w ≦ u a {v, w} je hrana. Snadno lze dokázat, že zobrazení l a p definují vrcholové stromy s množinou uzlů U, s množinou všech možných hran tvaru {u, l(u)}, resp. {u, r(u)} a s minimálním, resp. maximálním uzlem jako s vrcholem. Nazveme je levým a pravým vrcholovým stromem stromu (U, H) s uspořádáním uzlů <.[15]

Všimněme si stromu a uspořádání uzlů věty (1). Dostáváme l(kufr) = můj, l(domů) = [24]l(můj) = odvézt, l(odvézt) = slíbil, l(bratra) = tvého, l(slíbil) = l(tvého) = přítel; p(přítel) = p(tvého) = bratra, p(bratra) = slíbil, p(slíbil) = odvézt, p(odvézt) = p(můj) = kufr, p(kufr) = domů. Oba vrcholové stromy lze potom znázornit např. takto:

Lze dokázat, že každý hladký strom je dvojicí svého levého a pravého vrcholového stromu jednoznačně určen. Zvolíme-li v hladkém stromu nějaký uzel za vrchol, lze o tom, zda takto vzniklý vrcholový strom je projektivní, rozhodovat z podoby levého a pravého vrcholového stromu, tedy z podoby zobrazení l a p. Vzhledem k zajímavým vlastnostem těchto zobrazení je přirozené klást otázku, lze-li pro ně nalézt lingvistickou interpretaci.

 

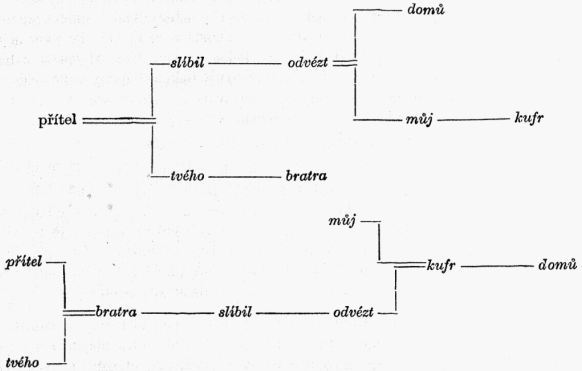
Otázky, které zde byly položeny, vycházejí z jednotného pohledu na formální aspekty závislostní struktury věty. Tento pohled, který se opírá o vlastnosti formulovatelné v teorii neorientovaných grafů, nebýval obvyklý.[16] Navíc jsou tyto otázky inspirovány matematickými výsledky, které většinou nejsou nasnadě. Stěží lze tedy očekávat, že bude jednoduché těchto pět otázek zodpovědět.

 

R É S U M É

Some Questions of the Dependency Conception of Syntax

The article is based mainly on the author’s previous study of some formal aspects of the dependency conception of syntax. Five questions are put concerning mathematical concepts and their application in linguistics.

1. The dependency structure of sentence can be described in a well-known way by means of a rooted tree. Is it possible to characterize in some general way the sentences, in the tree of which the root is situated in the proximity of center (mass center) in opposition to those sentences, in the tree of which the root is considerably removed from the center (mass center)?

[25]2. If the vertices of a rooted tree of sentence are ordered in agreement with its word order it is relevant to ascertain, whether the rooted tree is projective. The projectivity can be proved, if and only if the following conditions are simultaneously fulfilled: (1) the root is situated on an undirected arc connecting the minimum (first) vertex with the maximum (last) vertex of the ordering; (2) if {p, q} and {r, s} are two undirected edges and if in the ordering the vertex r follows the vertex p, but precedes the vertex q, then the vortex s is either identical with the vertex q or precedes it (cf. the citation in note 9). The second condition is apparently independent of the choice of root. The tree having this quality is called a smooth tree. There is another question which can be verified only empirically: Is it true that the not too short unprojective sentences we meet in texts are usually not smooth?

3. An undirected arc in a tree with ordered vertices connecting the minimum and maximum vertices will be called the chief arc. From the formal standpoint this arc has an exceptional position. Is it true that the chief arc of the sentence tree is usually significant for the sentence construction in the sense that in some of its most important features the sentence may be determined by this more conclusively than by any other equally long arc?

4. The smoothness and the projectivity are connected with each other in an other way, too. In a certain sense it is possible to examine the projective tree of a sentence as an ordered pair of smooth trees with an only common vertex. The parts of sentence correspond to each of these smooth trees. How should these sentence parts be linguistically characterized?

5. Let us consider a tree with ordered vertices containing a vertex u. If this is no maximum vertex, we denote as p(u) the vertex which — with regard to the given ordering — is situated to the vertex u nearest of all those vertices following the vertex u and at the same time is connected by means of an undirected edge either with vertex u or with an other vertex preceding the vertex u. If the vertex u is no minimum vertex, it is possible to define analogically the vertex l(u), if “followed” is replaced by “preceded”, and inversely. It is possible to show that by the formal examination of smooth trees the mappings l and p play an important part. Is it possible to find a linguistic interpretation for them?

Slovo a slovesnost, ročník 32 (1971), číslo 1, s. 20-25

Předchozí Eugenius M. Uhlenbeck (Leiden): Nové výsledky vývoje transformační generativní gramatiky (kritický přehled)

Následující Josef Hrbáček: Citátové výrazy a jiné periferní lexikální prvky cizího původu v slovní zásobě češtiny