
Na okraj Herdanových knih o kvantitativní lingvistice
Oddělení matematické lingvistiky v ÚJČ
[Discussion]
По поводу книг Хердана о количественной лингвистике / A la marge des livres de Herdan sur la linguistique quantitative
Už pět knih vyšlo z péra známého statistika, resp. lingvistického statistika Gustava Herdana: Language as Choice and Chance, Groningen 1956 (srov. SaS 20, 1959, 44n.); Type-Token Mathematics, ’s-Gravenhage, Mouton 1960, 448 s. (dále jen Type-Token); The Calculus of Linguistic Observations, ’s-Gravenhage, Mouton 1962, 271 s. (dále jen Calculus); Quantitative Linguistics, London, Butterworths 1964, 284 s.; The Advanced Theory of Language as Choice and Chance, Berlin—Heidelberg—New York, Springer Verlag 1966, 459 s. (dále jen Advanced Theory).
Od Yulovy práce Statistical Study of Literary Vocabulary (Cambridge 1944; srov. SaS 27, 1966, s. 366) a převážně na problematiku slovníku zaměřených studií Guiraudových[1] nevyšla, pokud víme, kniha systematicky pojednávající o jazyce z hlediska [59]statistiky. G. Herdan do jisté míry navazuje na Yulovu studii a využívá často i jejího materiálu.
Kromě toho přinášejí Herdanovy knihy jistý přehled málo dostupné literatury a do jisté míry i informace o vývoji statistické lingvistiky.
Pokud jde o tematiku, jsou Herdanovy knihy uspořádány cyklicky, jejich znalost se většinou navzájem nepředpokládá. Proto se jednotlivé tematické celky v nich ve větší nebo menší míře opakují. Jsou to v podstatě tyto: statistika fonologická, statistika slovníková a stylistická (problematika slovníku) a teorie informace. K nim pak v jednotlivých knihách přibývají témata další, např. kvantová teorie jazyka (v kn. Calculus, s. 179—211) i praktické užití statistiky (v kn. The Advanced Theory, s. 371—437) apod. Relativně nejsamostatnější celek tvoří kniha Quantitative Linguistics, poslední kniha The Advanced Theory je upravená a doplněná kniha první (z r. 1956), jak ostatně je uvedeno v jejím titulu.
Herdanův přístup k jazyku se celkem důsledně opírá o některé starší myšlenky strukturální lingvistiky, zvl. pražské školy: Je to učení F. de Saussura o dichotomii langue a parole, rozlišování signifiant a signifié apod. Herdan zná i binarismus Jakobsonův, pokouší se vyrovnat i s některými myšlenkami Hjelmslevovými (srov. „plane of expression“ a „plane of content“ v kn. Calculus, s. 230, 246) apod. Je pochopitelné, že se jako nelingvista Herdan někdy nedostane za termíny, ale je třeba přiznat, že celkem citlivě pracuje s jazykovými jevy a snaží se respektovat složitost jejich vztahů a jejich hierarchii. Herdan sice vychází od jazykových jednotek, jakými jsou foném, grafém, morfém, slovo (v aplikaci na deskriptivní geometrii odpovídají bodu), ale všímá si i větších celků vzniklých opakováním těchto jednotek-bodů (jako paralel k přímce), konečně i nejvyšší jednotky textu, kontextu (paralela k ploše).
Základním technickým aparátem při studiu jazyka je Herdanovi matematická statistika. Nepokládá ji za samoúčelnou, neboť jazyk už ve své podstatě je statistický soubor. Statistické metody jsou proto podle Herdana nedílnou a nutnou částí metod studia jazykové struktury. Lingvistické jednotky (slova, fonémy aj.) vnímáme jako časté, méně časté a řídké jevy, vnímáme možnost jejich spojování, tzn., že je chápeme statisticky; proto jejich zpracování a hodnocení vyžaduje statistiku, pravděpodobnost a kombinatoriku. Na podporu této skutečnosti se Herdan často dovolává německého fyzika E. Schrödingera, zvláště jeho knihy Statistická termodynamika, v které Sch. např. říká: „… jedním z překvapujících rysů statistické termodynamiky (která představuje prototyp statistické teorie informace) je, že veličiny a funkce, původně zavedené jako matematické hodnoty, téměř beze změny získávají základní fyzikální význam“ (Calculus, s. 103).
Zvláštní zmínky pak zaslouží v knihách Herdanových princip duality jakožto základní motiv vystupující s větší či menší naléhavostí téměř v každé kapitole. Princip duality H. chápe jako ústřední zákon dialektiky myšlení, jehož manifestací je soustava protikladů — v logice zákon Boolův (jestliže x (1 — x) = 0, pak x2 = x), ve fyzikální statistice protiklad mezi klasickou a kvantovou teorií, v deskriptivní geometrii vztah mezi bodem a přímkou. V lingvistice H. připomíná kromě uvedených protikladů langue — parole a signifiant — signifié i vztahy jazyková jednotka — její výskyt (type-token), pravděpodobnost v základním souboru — četnost ve výběru a dále objektivní nahodilost — subjektivní volba (chance — choice). Soustava těchto binárních relací, které se v duchu Hegelovy dialektiky, jak H. připomíná, vzájemně prostupují a jejichž komponenty si vyměňují místa, zařazuje kvantitativní lingvistiku do soustavy přírodních a společenských věd, spojuje je s nimi metodologicky a dává jim obecnou filosofickou základnu. Kompozice Herdanových výkladů je pak dána souvislostmi mezi jednotlivými komponenty těchto relací, které se v různých kapitolách stávají dominantními a soustřeďují kolem sebe repertoár statistických metod. [60]Ty však nepředstavují jádro Herdanových knih, ale slouží spíše jako ilustrace autorových obecně metodologických předpokladů. Výklad jednotlivých komponentů duality pak vychází od objektivních kvantitativních vlastností systému a textu (chance) a vrcholí — ve shodě s hegelovským pojetím — rozborem individuálního stylu. Herdanovy knihy tedy nejsou soupisem statistických technik, ale stávají se výkladem metodologie a „filosofie“ kvantitativní lingvistiky. Avšak složitost kompozice a snaha o důsledné uplatňování obecně fungujícího dualismu Herdanův výklad mnohdy spíše rozrušují a znejasňují, než aby jej podporovaly. Užitečné (a značnou autorovou erudicí poznamenané) zasazení pojmů kvantitativní lingvistiky mezi obecné kategorie abstraktního myšlení, které se projevují pouze s nepatrnými modifikacemi ve všech společenských i přírodních vědách, není tu vždy vyváženo vysvětlením specifičnosti předmětu zkoumání a vymezením lingvistické problematiky, která má — spolu se vztahy k ostatním vědeckým disciplínám — svou vnitřní logiku a strukturu.
Základem izomorfního chápání lingvistiky a obecné teorie fyzikálních systémů je vztah dvou typů statistik, z nichž každá se uplatňuje v jiném jazykovém plánu. Obecně lze říci, že makrostav fyzikálního souboru (v lingvistice základní soubor) je určen jistým počtem mikrostavů (v lingvistice výběrů), vzájemně ekvivalentních, jejichž počet udává termodynamickou pravděpodobnost makrostavu. Statistika klasického typu (Boltzmannova - Maxwellova) rozlišuje nejen jednotlivé prvky systému, ale i jeho dílčí soubory. Tato klasická statistika, užitá např. C. Shannonem pro oblast fonologie a grafematiky, je méně vhodná pro měření vlastností slovníku, pro který H. navrhuje statistiku Fermiho-Diraca, která nebere v úvahu odlišnost jednotlivých prvků zkoumaného systému, ale jejich vztah, asociace (v případě kvantové fyziky elektronů, neutronů a protonů), a statistiku Boseho-Einsteina, která navíc nerozlišuje ani jednotlivé mikrostavy systému. H. tak postuluje obecné rysy kvantových elementů i slov v lexikální soustavě, která se mnohdy zřetelně neodlišují ani četností ani rozložením ve výběrech. Jedním z příznačných rysů Herdanových výkladů je přesvědčení o bezprostřednosti vztahu mezi číselným lingvistickým údajem a jeho interpretací.
Tento vztah je však podle našeho názoru daleko méně přímočarý; číslo v lingvistice je pouze předpokladem interpretace, která se opírá o výsledky různé statistické spolehlivosti a nestejného věcného významu. Kvantitativní analýza více naznačuje tendence řešení a ponechává možnost úvaze lingvisty, hypotézy spíše nezamítá, než dokazuje. Proto také některé Herdanovy příklady, metodologicky cenné, jsou charakteristické jistým „krátkým spojením“ mezi číslem a výsledným soudem. Platí to např. i o instruktivním a lingvisticky zajímavém užití faktorové analýzy (Calculus, s. 86—92, The Advanced Theory, s. 445n.) jako metody klasifikace jazyků založené na počtu slovních kořenů společných jistým skupinám ide. jazyků. Korelace slovníkových údajů pro jednotlivé jazyky s obecným faktorem (v termínech faktorové analýzy se tu mluví o saturaci, nasycení klasifikovaných individuí jistou základní vlastností, v tomto případě ide. slovníkem) mohou naznačovat typologická kritéria, ale samy je neutvářejí, zvl. ne proto, že podkladem třídění je zde pouze jistá vrstva slovníku. Samo užití faktorové analýzy je však názorné a poměrně přesvědčivé, lze jen litovat, že právě zde autor podrobněji nerozvádí vysoce náročný aparát této metody, která se v poslední době přestává omezovat na psychologické aplikace a zaujímá významné místo mezi metodami kvantitativní lingvistické taxonomie.
Všimněme si nyní jednotlivých tematických okruhů, s nimiž se v jednotlivých Herdanových knihách setkáváme:
Fonologická statistika. Vzhledem k tomu, že kvantitativní fonologie patří do oblasti statistické lingvistiky, která se řídí zákonitostmi náhody a lze na ni aplikovat stejné statistické postupy a metody jako na ostatní náhodné jevy, zařazuje ji H. téměř do všech svých prací. Náhodnost nižších jazykových jednotek (druhého členění) dovoluje užít [61]pro získání materiálu nejrůznější výběrové postupy, jsou-li nezávislé na hledané charakteristice. V úvodu autor zdůrazňuje, že jazyková statistika poskytuje lingvisticky relevantní informaci především tehdy, můžeme-li porovnat získané hodnoty se standardem. Příkladem takového porovnání je např. četnost fonému v určité pozici a jeho celková četnost, počet různých slov, kde foném má rozlišovací funkci a všechna slova v slovníku, která tento foném obsahují, aj. Standardem může být např. celková četnost fonému, počet teoreticky možných výskytů fonému v dané pozici, pravděpodobný interval variability jazykového rysu, tj. variabilita v mezích náhodnosti, apod. Pozorované četnosti jazykových jednotek nabývají lingvistické hodnoty právě ve vztahu k hodnotám teoretickým. Poměrem pozorované četnosti k četnosti teoretické vyjadřuje pak H. míru funkčního zatížení fonému (v slovníku). Porovnává pak statistiku fonémů v slovníku se statistikou fonémů v textu. Užitečnost takového přístupu zdůraznil již Trubecký (v Grundzüge der Phonologie, 1939).
Statistické zkoumání fonémů na základě slovníku (a) udává, v jaké míře přispívají jednotlivé fonémy k rozlišení významu, jaké je funkční zatížení fonémů apod.; naproti tomu (b) statistické zkoumání fonémů na základě souvislého textu odhaluje diferencované využití realizovaných jednotek. Lze pozorovat, že slovní typy s vysokým procentem realizace teoreticky možných kombinací fonémů mají nižší relativní četnost než slova opačného druhu. — Takto získané charakteristiky slouží k typologické klasifikaci jazyků, jak se o ni mezi prvními pokusili Mathesius a Trnka.
Významné poznatky o fonologické rovině jazyka přináší studium statistického rozložení fonologických opozic. Jako příklad uvádí H. utřídění a hodnocení některých opozic (jednorozměrné a vícerozměrné, proporcionální, izolované) vzhledem k ostatním opozicím v systému, počet fonémů, které se jednotlivých opozic účastní apod.
Zvláštní pozornost věnuje H. i analýze vztahů mezi funkčním zatížením fonémů a četností jejich výskytu. Studuje ji metodami kvantitativní lingvistiky a na podkladě své teorie o slovníku jako základním souboru jazykových jednotek a textu jako jeho náhodném výběru dokazuje, že i na fonologické rovině jde o rozložení totožná. Své vývody ilustruje příkladem rozložení konsonantických fonémových tříd v jednoslabičných a dvouslabičných slovech Oxfordského slovníku (Trnka 1935, Krámský 1956) a rozložením fonémů v souvislém textu (údaje z Fowlera 1957). Statistické testování jednotlivých rozložení opět ukazuje, že poměr jazyková jednotka : její výskyt u fonémů není významně ovlivněn stylem, tj. že rozložení fonémů nejen v různých druzích souvislého textu, ale i v textu a slovníku je tak málo odlišné, že je lze považovat za stabilní. Tato stabilita dovoluje na základě Poissonova zákona řídkých jevů odvodit rozložení jednotek v textu z jejich rozložení v slovníku.
Funkční zatížení v slovníku se jeví jako dominantní faktor, jímž se řídí využití fonémů v řeči. Vztah mezi fonémy a jejich kategoriemi z hlediska funkčního zatížení je pro jazyk specifický — můžeme rozlišit mluvené jazyky, i když je přímo neznáme. Jako příklad uvádí H. rozložení fonémů podle způsobu a místa artikulace v pěti jazycích (podle materiálu Krámského) a v mluvené řeči (materiál mu poskytli French, Carter a Koenig).
Vztah mezi rozložením v slovníku a v textu u vyšších jazykových kategorií nebyl dosud podrobněji studován. Herdan si vybírá kategorii slovní délky vyjádřené počtem fonémů nebo grafémů a na ní se pokouší dokázat vztah analogický k vztahu základního souboru a výběru, který byl zjištěn u fonémů a grafémů. Williams (1940, 1946) empiricky odvodil, že některá lingvistická rozložení jsou logaritmicky normální. H. přijímá toto zjištění jako hypotézu pro studium slovní délky. Jako ověřovacího materiálu se zde opět užívá statistiky Frenchovy aj. H. pak dospívá k dvěma významným tvrzením: (1) rozložení slovníku a textu podle délky slov vyhovuje kritériím logaritmické normality; (2) rozložení textu je momentem rozložení slovníku (pro délku slov). (Praktický význam tohoto zjištění je výpočtářský; známe-li jedno rozložení, můžeme [62]vypočítat druhé.) Metoda odvození však vychází z předpokladu, že vztah mezi frekvencí slova a jeho délkou je inverzní, což se zdá být předpokladem příliš silným; takový vztah platí v různé míře podle zkoumaného materiálu.
Statistika slovníková a stylistická. Jednotkou jakéhokoli statistického výběru jazyka je u Herdana slovo. Text má podle něho všechny znaky statistického základního souboru a jeho jednotka (slovo) má rozložení v podstatě náhodné. Struktura slov, jakožto náhodná kombinace písmen, závisí na počtu základních fonémových nebo abecedních prvků a na možnostech jejich kombinování ve vyšší jednotky. Jazyk klade určitá omezení, má své vlastní zákonitosti (tím se liší od kódu), např. všechny kombinace písmen nejsou přípustné, kombinace samohlásek jsou velmi omezené, opakování písmen kromě zdvojení je vyloučeno. Další omezení náhodného kombinování písmen je způsobeno tím, že písmena nemají stejnou frekvenci. V západoevropských jazycích zhruba 14 písmen odpovídá 85—95 % výskytu písmen, např. angl., franc., němč. (v češtině představuje 14 nejčetnějších písmen 67,64 % všech výskytů).
Pokud jde o slovník ve vlastním slova smyslu, věnuje H. zvláštní pozornost studiu jeho struktury a spojuje ji zpravidla s tzv. stylistickou statistikou. Navazuje tu do značné míry především na Yula (opírá se i o jeho materiál), tedy na zaměření „textologické“, zabývá se jeho charakteristikou K a dále ji upravuje.[2] Hodnotí ji jako míru stylistické různosti, danou poměrem mezi jednotou a růzností frekvence slov (Quantitative Linguistics, s. 71), a propracovává ji jako charakteristiku danou vzorcem
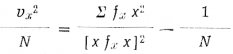
Mnoho pozornosti věnuje H. i distribuci slov podle jejich frekvence, především klasickému dnes tzv. zákonu Zipfovu i jeho úpravě Mandelbrotově v tzv. kanonický zákon, a vytýká jim oběma nedostatky z hlediska teoretického i praktického (zejm. pokud jde o r, tj. pořadí slova).[3]
Na základě studia rozložení slov uspořádaných podle klesající frekvence dochází H. k závěru, že pro slova s největší frekvencí platí rozložení binomické, kdežto pro slova se „střední“ frekvencí rozložení Poissonovo s opakováním, pro slova s nejnižší frekvencí pak jednoduché rozložení Poissonovo. Autor si je dobře vědom toho, že frekvence slov závisí na asociaci se slovy jinými, že na jejich výběr má do značné míry vliv téma a styl. K vyjádření této závislosti užívá např. Pearsonova koeficientu kontingence. Zejména pak kvantová teorie umožňuje podle Herdana studovat frekvenci slov ve vztahu k charakteru textu (srov. např. Calculus, s. 211). Kromě toho užívá H. ve studiu slovníku i charakteristik teorie informace, srovnává rozložení frekvenční a slovníkové se zřetelem k informaci, která je v nich obsažena. Na základě zákona velkých čísel užívá entropie (I) místo průměru (M). Větší entropie neznamená tu více informace a tím výhodnější kód, ale znamená v dnešním pojetí (srov. Bernouille aj.) míru neočekávanosti (negentropie).
Pokud jde o materiál, o nějž se opírá H. v analýzách slovníkové a stylistické statistiky, je třeba litovat, že se tu opakuje zmíněný již materiál Yulův (sebraný k problémům celkem čistě textologickým), materiál slovníku R. Morgenthalera (Statistik des Neutestamentlichen Wortschatzes, Zürich — Frankfurt am Main 1958), vzatý z prací již publikovaných. Domníváme se, že jiný slovníkový materiál a jeho statistická analýza by autorovi ukázala řadu dalších problémů, s nimiž se musíme vyrovnat v lexikální statistice. Tzv. stylistická statistika by pak vyžadovala samostatná řešení, i když její těsný vztah k statistice slovníku nelze jistě pominout.
[63]Teorii informace věnuje H. ve svých knihách zpravidla samostatný oddíl. Vychází z předpokladu, že jazyk můžeme považovat za složitý kódovací systém, jehož prvky jsou různé lingvistické jednotky z různých jazykových rovin (fonémy, morfémy, slova atd.), v nichž existuje (1) stabilita četnosti nebo pravděpodobnosti těchto jazykových jednotek a že (2) uspořádání těchto jazykových jednotek je podřízeno kombinatorickým zákonům. H. pokládá lingvistický přínos teorie informace za problematický a snaží se ukázat, že binární systém je vhodný k popisu lingvistických kódů, poněvadž může být interpretován jako formální výraz rozlišovacího principu fonologie, jinými slovy jako matematické vyjádření fonologické opozice. Zkoumá efektivnost jazykového kódu a odvozuje základní teorém teorie informace: podmínkou efektivního kódování nebo efektivního přenosu informace je, že průměrná délka kódové jednotky u dlouhých sdělení nesmí být menší než H, čili
H ≦ x̅ < 1 + H
Charakteristickým rysem aplikace teorie informace na jazyk je reciproční vztah mezi délkou kódové jednotky a pravděpodobností výskytu, což je základem hodnocení optimálního kódu. H. odvozuje entropii z multinomického rozložení a nachází různé vztahy mezi entropií, indexem opakování a Yulovou konstantou.
Kromě toho se zabývá analýzou binárního principu odpovědí, který má své lingvistické opodstatnění a byl užit Jakobsonem k zakódování fonologického systému. Ukazuje, že je značný rozdíl v interpretaci entropie podle typu lingvistických jednotek, z nichž je počítána. Veličina H (entropie) spočítaná z posloupnosti fonémů bude vždy větší než ze slov o různém počtu fonémů, a to z těchto důvodů: (1) čím delší je posloupnost, tím větší je entropie, (2) fonémy se nemohou kombinovat nezávisle, existují omezení daná jazykem co do spojování fonémů a jejich pozice v slově.
Rozdíl mezi entropií vypočítanou pro nezávislou posloupnost fonémů a entropií, v níž se přihlíží k relativním četnostem fonémových digramů, trigramů atd., je mírou strukturního prvku jazyka. Umožňuje nám to srovnávat objektivně jazyky, místo abychom se spoléhali na subjektivní dojmy, které jsou přirozeně odlišné. Srovnávání jazyků z tohoto hlediska zvláště ve vztahu k binárnímu překladu věnuje H. v svých posledních knihách mnoho pozornosti.
Statistika a jazyková struktura patří k ústředním tématům, s nimiž se v Herdanových knihách rovněž setkáváme. Zvláštní pozornost mu věnuje zejm. v kn. Calculus a The Advanced Theory. Rozlišuje dvě velké oblasti užití statistických metod při studiu jazyka: jedna, v níž se statistiky užívá jako pomocného nástroje, hlavně k testování hypotéz, a druhá, v níž problémy samy jsou kvantitativní povahy, a proto vyžadují k řešení statistické metody. Matematické metody potřebné k tomuto účelu nazývá H. kalkulem lingvistických pozorování. Vztah textu k jazyku je stejný jako vztah výběru k základnímu souboru. Příkladem lingvistického vztahu kvantitativní povahy je vztah mezi statistikou souvislého textu a lexikální statistikou. Langue má podle Herdana charakteristické rysy statistického základního souboru; pravděpodobnosti náhodné proměnné se uskutečňují v náhodných výběrech, parole lze tedy ztotožnit se statistickým výběrem.
Na škodu Herdanových prací je mimo jiné to, že se při postupu od základního souboru k výběru a naopak užívá nedůsledné symboliky (jednou označuje rozsah výběru m, podruhé n), což vede k nepřehlednosti složitých výrazů pro výpočet pravděpodobnosti. Kladně je však třeba hodnotit, že Herdanovy práce podávají souhrnný přehled o matematickostatistických metodách aplikovaných na jazyk. Začíná se elementárním způsobem, tj. popisnou statistikou, uvádějí se charakteristiky polohy (modus, medián, aritmetický průměr aj.), podotýká se, že jsou na sobě nezávislé v tom smyslu, že nemůžeme odvodit jednu charakteristiku z druhé. Jejich hodnoty se shodují pouze u symetrického rozdělení. Rozdílem průměru a modu (nejčetnější hodnoty znaku) odhadujeme šikmost rozdělení. Neurčujeme pak jen konstanty, ale přímo typ [64]rozdělení, empirická rozdělení potom srovnáváme s Gaussovým neboli normálním rozdělením jako s normou. H. podrobně probírá tři hlavní typy statistických přístupů: (1) od velkého souboru (základního souboru) k menšímu (výběru), (2) od menšího souboru k většímu (od výběru k základnímu souboru), (3) od jednoho výběru k druhému. Na základě kombinatorické analýzy odvozuje vzorce pro pravděpodobnosti.
Zajímavý je oddíl o teorii korelace. H. zde rozlišuje funkční vztah (závislost), která se vyskytuje např. ve fyzice a chemii, od statistické závislosti (korelace), platící např. v biologii, medicíně, psychologii a v lingvistice. Zde většinou nejde o jednoznačné přiřazení hodnot závisle proměnné hodnotám nezávisle proměnné, nýbrž každá hodnota proměnné x nebo y je pouze jednou z celé řady možných hodnot kolem průměru. V tom je rozdíl mezi funkčním vztahem a statistickou korelací. Koeficient regrese, jakožto jednostranná míra statistické vazby, nám umožňuje předvídat změnu závisle proměnné na jednotku nezávisle proměnné. Oboustrannou mírou je koeficient korelace, proto je k měření závislosti vhodnější. Koeficientem asociace můžeme měřit také těsnost vazby jedné proměnné na druhé (např. ve slovníku).
Závěr: Podat ucelený obraz o kvantitativní lingvistice jak z hlediska matematické statistiky, tak i z hlediska lingvistického je cíl neobyčejně záslužný, ale zároveň tak náročný, že přesahuje síly jednotlivce. A přece se o něj pokusil G. Herdan, i když jen v titulu jedné knihy (Quantitative Linguistics) je tento cíl jasně vyjádřen. Ačkoli se autor ve srovnání s jinými matematiky, kteří se zabývají matematickou lingvistikou, dostal ve vztahu k lingvistice, orientaci v ní i v poměru k jazykovým jevům nejdále, nezapřou jeho knihy přístup matematika. Interpretace statistických údajů a šetření jsou sice správně proklamovány, ale autor se v nich příliš daleko nedostal. Je to zřejmě dáno i tím, že se autor téměř ve všech svých knihách opírá o týž materiál, většinou pak opět přejatý z jiných prací. Opakování týchž tematických okruhů v jednotlivých knihách dává sice možnost užívat jednotlivých knih do jisté míry zcela samostatně, na druhé straně však knihy jednotlivě i jako celek ztrácejí na přehlednosti a jasné stavbě, uživatel se v nich nesnadno orientuje. Větší soustředění, jemuž se autor nejvíce přiblížil v kn. Quantitative Linguistics, upuštění od množství jednotlivostí často problematických a polemicky zaměřených (srov. o. c. v pozn. 2) apod., bylo by jen na prospěch věci — kvantitativní lingvistiky, pro niž autor nesporně mnoho vykonal. Podstatné a sympatické jsou Herdanovy myšlenky, že statistiky není v lingvistice nikdy dost a že lingvistika potřebuje vlastní statistické metody.
[1] Pierre Guiraud, Les caractères statistiques du vocabulaire, Paris 1954; týž, Problèmes et méthodes de la statistique linguistique, Dordrecht 1959.
[2] Srov. též G. Herdan, A New Derivation and Interpretation of Yule’s „Characteristic K“, Journal of Applied Mathematics and Physics 6, 1955, 332.
[3] Srov. též Mandelbrotovu kritiku Herdanovy knihy Type-Token v časop. Information and Control 4, 1961, s. 88—95 a odpověď Herdanovu tamtéž, s. 239—240.
Slovo a slovesnost, volume 28 (1967), number 1, pp. 58-64
Previous Milena Koubková: Algoritmus dílčí analýzy matematického textu (pro automatický překlad z ruštiny do češtiny)
Next Ludmila Uhlířová: K statistickému zkoumání slovosledu
© 2011 – HTML 4.01 – CSS 2.1