
Ke kvantifikaci homonymie
Pavel Novák
[Chronicles]
К вопросу о квантификации омонимии / Quantification des homonymes
[*]V posledních letech se setkáváme s pokusy kvantitativně charakterizovat typologické rysy jazyků.[1] Zračí se v tom přirozený vývoj typologické teorie: když byly starší pojmy klasifikační nahrazeny pojmy pořádajícími, dochází se k pojmům kvantitativním (metrizovaným).[2]
[73]Nedávno zavedl rumunský lingvista Sorin Stati[3] tři charakteristiky morfologické homonymie.
1. Maximální počet forem, které mohou být homonymní v p paradigmatech o f kategoriích[4] (pádech, osobách etc.). Označme jej symbolem K. Stati se domnívá, že mezi veličinami K, p a f obecně platí vztah vyjádřený tímto vzorcem:
K = f . p — f (1)
Příklad 1. 1. Mějme 2 paradigmata a 2 kategorie. Tedy
K = 2 . 2 — 2 = 2
Můžeme však uvést tento příklad:
|
| I | II |
| A | a | a |
| B | b | a |
Vyskytuje se v něm a 3krát, tedy více, než předpokládá Stati. Např. v nové angličtině je dvěma formami, sing — sings apod. zaručen jednak protiklad osob („první-druhá“ : „třetí“), jednak protiklad čísla. Uvedený vzorec pro tento příklad tedy neplatí.
Příklad 1. 2. Mějme 4 paradigmata a 2 kategorie. Tedy
K = 2 . 4 — 2 = 6
Znázorníme-li si opět situaci, máme
|
| I | II | III | IV |
| A | a | a | b | a |
| B | a | b | a | c |
Vidíme, že a může být nejvíc 5krát (tedy méně, než předpokládá Stati), v každém jiném případě by splynula aspoň dvě paradigmata vjedno. Uvedený vzorec pro tento příklad tedy také neplatí.
Stati k vzorci zřejmě došel z příliš omezujícího tvrzení, že je „homonymie některých flexívních forem f1, f2, .., fn (vyjadřujících n kategorií - P. N.) v témž paradigmatu možná jen tehdy, když má daný jazyk více paradigmat a aspoň jednou je každá z forem f1, f2, … fn ve formálním i významovém protikladu ke všem (proložil P. N.) ostatním formám paradigmatu“ (26). Slovo forma tu vlastně může znamenat buď celý slovní tvar (jako např. v příkladě 1.1), nebo afix (jako např. v příkladě 1.2). Avšak v obou (i v jiných) případech je prostě logicky nemožné, aby všechny formy několika paradigmat byly zcela homonymní, mají-li to být různá paradigmata.
Uvedeme nyní vzorec pro výpočet K, který nemá nevýhody Statiho vzorce. Označme větší z čísel f a p jako α a menší jako β. Pak
K = α (β — 1) + 1. (1’)
2. Maximální počet homonym řádu x v počtu p paradigmat o f kategoriích (řádem homonyma se tu rozumí počet kategorií, které homonymní tvar vyjadřuje). Stati pro tuto veličinu (Kx) uvádí opět jistý vztah, vyjádřený tímto vzorcem:[5]
![]() (2)
(2)
Ani tento vzorec neplatí obecně.
Příklad 2.1. Mějme 3 paradigmata, 6 kategorií, homonymii 3. řádu.
Tedy
![]()
Stati sám uvádí tento případ (v jiné symbolice):
|
| I | II | III |
| A | a | c | g |
| B | a | c | h |
| C | a | c | i |
| D | b | d | j |
| E | b | e | j |
| F | b | f | j |
[74]Zde jsou opravdu 4 homonyma 3. řádu.
Můžeme však uvést příklad, v němž za stejných podmínek je 6 homonym 3. řádu:
|
| I | II | III |
| A | a | c | e |
| B | a | d | e |
| C | a | d | f |
| D | b | d | f |
| E | b | c | f |
| D | b | c | e |
3. V další části článku definuje Stati procento homonymické redundance (HR). Převedeme jeho slovní formulaci (28) do vzorce.
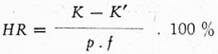 (3)
(3)
K — viz odstavec 1, K' — počet forem, které jsou homonymy aspoň 2. řádu.
Stati propočítává hodnotu HR pro latinskou, starořeckou a novočeskou substantivní deklinaci (v singuláru).[6] V latině je 5 deklinačních paradigmat (casa = res, lupus, templum, lex = exercitus, nomen; Stati neuvádí cornu) a 6 pádů. Jak je z příkladů vidět, rozumí se tu jedním paradigmatem množina substantiv s totožnou soustavou homonym. V sg. jsou 2 homonyma 3. řádu (templum, nomen), 5 homonym 2. řádu (casa, casae, lupo, templo, lex). Tedy
K' = 2 . 3 + 5 . 2 = 16 a
![]()
V staré řečtině (s 4 paradigmaty a 5 pády) je HR 35%, v češtině (s 10 paradigmaty a 7 pády) podle Statiho 23% (1 homonymum 6. řádu, 2 homonyma 4. ř., 5 homonym 3. ř., 9 homonym 2. ř.), podle revize 20% (zjistili jsme totiž 10 homonym 2. ř.).
I k této části práce Statiho můžeme být kritičtí, ovšem v jiném smyslu než k prvním dvěma. Vzorce (1) a (2) udávají totiž vztah mezi jistými veličinami, jejichž hodnoty se dají v každém jednotlivém případě stanovit na sobě nezávisle. Jsou myšleny jako obecné výroky a my jsme obecnost každého z nich vyvrátili udáním aspoň jednoho protipříkladu. Jejich úlohou je zaměnit pracnou konstrukci od případu k případu jednoduchým výpočtem. Formule (3) je naproti tomu definicí (je to tzv. syntetická definice, jíž se zavádí nový pojem). Nemůžeme ji tedy vyvrátit, můžeme ovšem uvést některé její slabiny. Jedna slabina je zřejmá na první pohled: předpokládá se výpočet K podle kritizovaného vzorce (1). Při interpretaci paradigmatu, kterou tu má Stati na mysli (paradigma = množina substantiv s totožnou soustavou homonym), není však možno použít ani vzorce (1'), což je způsobeno tím, že pravidla stavby paradigmat v této interpretaci jsou odlišná od pravidel stavby paradigmat v běžné interpretaci. Objasníme si rozdíl na příkladu.
Příklad 3.1. Pro situaci
|
| I | II |
| A | a | b |
| B | b | a |
(v běžné interpretaci) protějšek v zmíněné interpretaci Statiho neexistuje.
Druhá slabina formule (3) je v tom, že K' má velmi malou charakterizační schopnost (K' má stejnou hodnotu pro případ s 2 homonymy 5. řádu i pro případ s 5 homonymy 2. řádu), a třetí v tom, že se ve vzorci odčítají veličiny nesourodé.
Stati upozorňuje, že výsledky studovaných tří jazyků ukazují na nepřímou úměrnost součinu f . p a HR a že se HR pohybuje kolem 30 %. V závěru pak vytyčuje další perspektivy, zejména použití navržené kvantitativní charakteristiky i pro diachronii. Ovšem vzhledem k uvedeným nedostatkům definice charakteristiky HR jsou všechny číselné údaje a tvrzení, které z formule (3) vycházejí, málo průkazné.
Statiho práce se řadí do širší skupiny prací, jejichž postup můžeme popsat asi takto. Pro všechny případy (systémy, jazyky) se zavede určitá extrémní veličina (např. u Statiho K) a pro jednotlivé případy se zjišťuje její vztah k jiné veličině, která již závisí na konkrétní jazykové realitě (např. u Statiho K'). Jako další takovou extrémní veličinu bychom mohli uvést minimální počet forem nutných pro zabezpečení morfologického (např. deklinačního) [75]systému o daném počtu paradigmat a kategorií. Označme si ji L.[7]
K podobným pracím je však třeba podotknout, že zdaleka ne všechny kvantitativní charakteristiky (ostatně jako charakteristiky vůbec) jsou stejně důležité (některé pak nemají důležitost vůbec žádnou). Opravdu důležité jsou jen ty, které vyhovují jistým požadavkům, tak zejména ty, u jejichž hodnot se podaří zjistit konstantní vztah k hodnotám jiných charakteristik,[8] dále ty, jejichž hodnoty jsou u mnoha jazyků nápadně blízké apod.
Přes všechny připomínky je nutno Statiho práci opravdu uvítat jako podnětný příspěvek při budování obecné teorie morfologických systémů, a to její formální části.[9]
Z matematických disciplín se v této teorii uplatní i kombinatorika, teorie grafů a statistika.[10]
[*] Děkuji dr. F. Zítkovi z Matematického ústavu ČSAV za cenné připomínky.
[1] Srov. J. H. Greenberg, A quantitative approach to the morphological typology, Methods and perspectives in antropology, Minneapolis 1954, 192—220. — E. P. Hamp, The calculations of parameters of morphological complexity, Proceedings of the eighth intern. congr. of ling., Oslo 1958, 134—142. — P. Sgall — P. Novák v přednášce Pražskaja tipologija jazykov i modeli jazyka, viz zatím Vjaz 9, 1960, č. 1, 132. — P. Sgall, Soustava pádových koncovek v češtině, Acta Universitatis Carolinae-Philologica 2, Slavica Pragensia II, Praha 1960, 65—84. — Zatímco Greenberg zkoumá text, zkoumají ostatní systém. — Srov. dále již G. K. Zipf, The Psycho-biology of Language, London 1936, 254n. a nejnověji několik statí v IJAL 26, 1960, č. 3 a 27, 1961, č. 4.
[2] Srov. V. Skalička, O současném stavu typologie, SaS 19, 1958, 230. — Z logického hlediska viz C. G. Hempel — O. Oppenheim, Der Typusbegriff im Lichte der neuen Logik, Leiden 1936. — C. G. Hempel, Fundamentals of concept formation in empirical science, Chicago 1952. Příklad na použití uvedených typů pojmů: klasifikačního — je teplo, pořádajícího — je tepleji než včera, kvantitativního — je 19° C. Již užití pořádajících pojmů umožňuje myšlenkově, popř. reálně — u znakových systémů — konstruovat typologické (vlastně lépe typové) extrémy, jak to činí významný polský logik K. Ajdukiewicz, zakladatel experimentální (konstruktivní) typologie jazyků; sestrojil jednak čistě „poziční“ jazyk, v němž se všechny syntaktické vztahy vyjadřují výlučně pozicí, jednak jazyk čistě „flexívní“, v němž se všechny syntaktické vztahy vyjadřují výlučně afixy — viz jeho stať Związki składniowe między członami zdań oznamujących, Studia filozoficzne 1960, 6 (21), 78—79. K podobným extrémům z hlediska logického srov. D. P. Gorskij, Idealizace a abstrakce, Pokroky matematiky, fysiky a astronomie 5, 1960, 741—750. Bylo by zřejmě užitečné pokusit se o axiomatizaci typologie (typologie v pojetí Skaličkově), zprvu patrně jen pro uměle zkonstruované typové extrémy. K myšlence experimentální typologie srov. i N. D. Andrejev, L. R. Zinder, Osnovnyje problemy prikladnoj lingvistiki, VJaz 8, 1959, č. 4, 14. — Srov. nyní i D. P. Gorskij, Voprosy abstrakcii i obrazovanije ponjatij, Moskva 1961, zejm. kap. VIII.
[3] V čl. Caracterul sistematic al omonimiei morfologice (Systémový charakter morfologické homonymie), Studii şi cercetări lingvistice 11, 1960, 25—31.
[4] Stati užívá termínu flexívní forma.
[5] Vzorec má u Statiho číslo 3. Mimo něj se v jeho práci uvádí ještě jiný vzorec (pod č. 2), který je však pouze jeho speciálním případem.
[6] Avšak jak postupovat při zjišťování HR v celé deklinaci?
[7] Označme opět větší z čísel f a p jako α a menší jako β. Pak L = nejmenší celé číslo větší než β-tá odmocnina z α nebo rovné této odmocnině. (4)
[8] Srov. V. Skalička, op. cit., 231.
[9] Jinou její součástí (významovou) je teorie morfologických protikladů. — Z dosud známých poznatků, spojujících obě právě uvedené oblasti, uveďme Brøndalovu hypotézu: „Si, à l’intérieur d’une catégorie donnée, une forme est définie de façon plus complexe que telle autre, cette dernière sera la plus différenciée“ (Essais de linguistique générale, Kodaň, 1943, 107; srov. duál v indoevropských jazycích).
Viz dále např. S. Ja. Fitialov, O postrojenii formal’noj morfologii v svjazi s mašinnym perevodom, Dokl. na konf. po obrabotke informacii, mašinnomu perevodu i avtomatičeskomu čteniju teksta, Moskva 1961, vyp. 2; I. L. Bratčikov, Nekotoryje teoremy formal’noj morfologii, tamtéž; K. Berka - P. Novák, Pokus o využití deduktivní metody k popisu ruské pádové soustavy, SaS 22, 1961, 203—208.
[10] Základní příručky pro kombinatoriku: E. Netto, Lehrbuch der Combinatorik, Lipsko 1901, J. Riordan, Introduction to Combinatorial Analysis, New York 1958; pro teorii grafů: D. König, Theorie der endlichen und unendlichen Graphen, Lipsko 1936, C. Berge, Théorie des graphes et ses applications, Paříž 1958; statistické příručky jsou všeobecně známé.
Ke kombinatorice: Např. vzorec (4) pro výpočet L je založen na vzorci pro výpočet variace s opakováním. K teorii grafů: Její aplikaci na probranou problematiku, jakož i na problémy příbuzné naznačil F. Zítek ve svém sdělení O aplikacích teorie grafů v lingvistice, předneseném na semináři o teorii grafů, organizovaném Matematickým ústavem ČSAV ve dnech 29.—31. května 1961 v Liblicích; soustavné matematické zpracování problematiky vyjde v čas. Aplikace matematiky. Ke statistice: Viz Statiho výklady částečně zde reprodukované v 3 — Na zmíněném semináři se vedle Zítkova sdělení týkal lingvistiky i referát K. Čulíka, V. Doležala, J. Prokopa a Z. Vorla Aplikace teorie grafů v elektrických obvodech, automatech a v lingvistice a sdělení P. Nováka a B. Palka Uplatnění teorie grafů v syntaxi přirozených jazyků.
Slovo a slovesnost, volume 23 (1962), number 1, pp. 72-75
Previous Pavel Trost: Vztahy mezi gnoseologií, logikou a jazykem
Next Vladimír Staněk: O jazyce nacistického Německa
© 2011 – HTML 4.01 – CSS 2.1