Informace o transformační gramatice

Bohumil Palek

[Discussion]

(pdf)

Сообщение о трансформационной грамматике / Information sur la grammaire de transformation

Lingvistika se za posledních let dostala pod vliv matematických metod, a to zejm. matematické logiky. Tento stav těsně souvisí s jednou stránkou lingvistického bádání — s praktickou aplikací matematické lingvistiky, jako je např. řešení různých komunikačních otázek, strojový překlad ap. V praktických aplikacích lingvistiky je dnes patrný zájem o rozpracování jejich teoretických podkladů, který je zároveň příčinou, proč je přehodnocována teorie lingvistiky vůbec, a to z hlediska některých nových poznatků metodologie vědy (srov. rozvedení metodol. principů N. Goodmana a W. O. Quina u Chomského). Využití matematických metod v lingvistice s sebou přináší i nový pohled na popis jazyka vůbec. Jedním z takových popisů, formálně rozpracovaným a přitom do jisté míry odpovídajícím intuitivnímu chápání gramatiky jazyka, je tzv. transformační gramatika (TG) vytvořená N. Chomským.[1]

[141]Pokusíme se podat výklad některých základních pojmů transformační gramatiky, pokud to vyžadují. Nepůjde o historiografické zjišťování pramenů, z nichž Chomsky při vytváření svého pojetí gramatiky čerpal, ani o zjišťování toho, co přejal od svých předchůdců,[2] nýbrž o to, zda cíl, který si stanovil, má pro lingvistiku teoretický nebo praktický význam a zda jeho teorie je k vyřešení těchto problémů dostačující. (Odpověď tu závisí na rozpracovanosti transformačních gramatik jednotlivých jazyků. Proto se také hodnocení může týkat jen perspektiv, které transformační gramatika poskytuje.)

Náš příspěvek má ráz především informativní. Pokud je to za dnešního stavu výzkumu transformační gramatiky češtiny možné, pokouší se podat i ukázku transformačních pravidel v češtině.

Úvod. Principy americké deskriptivní lingvistiky (někdy nazývané americkým strukturalismem), vyplývající vesměs z praktických požadavků na lingvistiku kladených (popis neznámých jazyků, techn. aplikace), jsou u nás dobře známy. Jedním z nejdůležitějších postupů mezi nimi je metoda větného rozboru analýzou na základě bezprostředních složek (immediate constituents), v základních požadavcích odlišnou od gramatiky závislostí u nás užívané (dependency grammar).

Na základě analýzy pomocí bezprostředních složek vznikla Chomského myšlenka rekurzívní výstavby gramatiky,[3] která ho přivedla k formulaci obecné teorie gramatiky, nejpodnětnějšího směru lingvistického zkoumání v poslední době, k formulaci generativní gramatiky, resp. jejích typů — gramatiky frázové (phrase-structure grammar, Chomsky 1961, a 1962: constituent structure grammar) a transformační (transformational grammar).[4] Analýzu na základě bezprostředních složek a gramatiku frázovou a transformační nelze ovšem klást z hlediska výzkumu do jedné roviny: v analýze na základě bezprostředních složek jde o zkoumání analytické, gramatika frázová a transformační jsou gramatikami generativními (generative grammar). Při analýze jazyka (srov. např. rozbor pomocí bezprostředních složek) jde o to, že v libovolné větě (tj. řetězci slov, fonémů nebo písmen přirozeného jazyka) umíme určit její strukturu (jinak řečeno, umíme provést rozbor větný) a nejvhodněji ji znázornit pomocí grafu - stromu, v němž můžeme sledovat např. hierarchické složení věty, její slovosled atd.[5] Taková analýza věty je dobře známa mimo jiné i ze strojového překladu, kde jsou nutné jisté odchylky ve srovnání s analýzou existující v běžné gramatice jazyka. (Při strojovém překladu má na analýzu vliv v binárním překladu jazyk, do něhož se překládá, při nezávislé analýze převodní jazyk.) Proto také jsou do určité míry (s uvedenými výhradami) oprávněna tvrzení, že algoritmus analýzy jazyka ve strojovém překladu má blízko k běžnému popisu jazyka.[6]

Gramatika frázová a transformační jsou gramatikami generativními. Generativní gra[142]matiku bychom charakterizovali asi takto: Je to takový soubor pravidel, který umožňuje odvozováním z určitého souboru výrazů generovat všechny věty přirozeného jazyka, které kdy byly vysloveny, a rovněž i ty, které ještě vysloveny budou (popř. i nebudou). Obvykle se říká, že je to aparát schopný generovat všechny a pouze všechny gramaticky správné věty daného jazyka a žádné jiné. Gramatická správnost vět přirozeného jazyka je dnes aktuálním problémem, o němž se živě diskutuje.[7]

1. Některé důležitější pojmy formálního aparátu transformační gramatiky. V našem popisu se zmíníme o základních pojmech transformační gramatiky, které jsou důležité při popisu jejího aparátu k sestavení generativní gramatiky konkrétního jazyka.[8] Transformační gramatika se skládá (především ve vztahu k syntaxi) ze dvou složek: složky frázové (phrase-structure component) a transformační (transformational component).[9]

Frázová složka. Frázová složka transformační gramatiky je svým formálním aparátem shodná s frázovou gramatikou. Proto podáme nejprve stručný přehled tohoto formálního aparátu frázové gramatiky (který již sám o sobě má stačit ke generování vět gramaticky správných) a příslušná omezení odlišující frázovou gramatiku od frázové složky transformační gramatiky uvedeme až po tomto výkladu.

Obecně jsou jednoduché frázové gramatiky (FG) definovány

(1)      FG = [V, + , V_T, → , S, #],

kde V je konečná množina symbolů — slovník (nikoli v běžně užívaném lingvist. smyslu; může jít např. o soupis morfémů ap.), + je relace sřetězení (concatenation), → dvoumístná, asymetrická, ireflexívní relace (pravidlo přepisování; Chomsky 1962), V_T je terminální slovník (tj. konkrétní slova přirozeného jazyka, S ∈ V_N, V — V_T = V_N), S je počáteční symbol při generaci věty, # ∈ V_T je symbol hranice věty.

Pomocí frázové gramatiky lze jak z prvků V_T, tak z prvků V_N (neterminální slovník) vytvářet řetězy. Mohou existovat různé typy frázových gramatik podle toho, jaká mají pravidla přepisování. Z lingvistického hlediska lze ovšem teoreticky uvažovat o generování typu

(2)      S → ψ,

kde o b_i ⋿ ψ (tj. symbol b_i je symbolem řetězu ψ) platí b_i ∈ V_T (tj. přímo z S je odvozen terminální řetěz, čili věta přirozeného jazyka). Prakticky je to ovšem nemožné, protože pro generování všech vět přirozeného jazyka bychom museli mít nekonečně mnoho pravidel (pro odvození každého terminálního řetězu jedno), a zároveň z lingvistického hlediska zcela nezajímavé. Proto se předpokládá existence slovníku V_N, který je soupisem gramatických kategorií (podmětová část, jméno, pád atd.; srov. odd. 2). Terminální řetěz (tj. řetěz obsahující pouze terminální symboly) je odvozován (derivován) z počátečního symbolu. Zároveň se žádá, aby tato derivace (derivation) byla provedena po konečně mnoha krocích, tj.

(3)      D = (φ₁, φ₂, …, φ_n),

[143]kde D je derivace terminálního řetězu φ_n, φ_i je řetěz, 1 ⩽ i ⩽ n, kde i, n jsou přirozená čísla. Vlastnosti jednotlivých frázových gramatik závisejí především na volbě pravidel φ → ψ, kterými je terminální řetěz odvozován. Konečně je třeba, aby při derivaci byl v řetězu přepisován při každém kroku pouze jeden symbol.

(4)      φ A ω → φ ψ ω,

kde A ∈ V_N je jediný symbol, φ, ω, ψ jsou řetězy.

Pravidlo typu (4) má v podstatě dvojí podobu:

(4a)      A → ψ,

kdy mluvíme o gramatice obsahující pouze pravidla (4a) jako o gramatice nekontextové (context-free grammar) a o pravidlu (4a) jako o pravidlu nekontextovém (context-free rule).

Druhá podoba pravidla (4) je

(4b)      φ A ω → φ ψ ω

Pravidlo se nazývá kontextové (context-restricted rule); gramatika užívající pravidel jak (4a), tak (4b) se nazývá kontextovou gramatikou (context-restricted grammar,[10] nebo také context-sensitive grammar, v. Chomsky 1962). V praxi při sestavování pravidel frázové i transformační gramatiky určitého jazyka je užití obojích pravidel nutné. Nekontextová pravidla jsou často nedostačující proto, že vyžadují zavedení nadměrného množství neterminálních symbolů, jestliže se chceme vyhnout generování vět gramaticky nesprávných. Lze dokázat, že existují jazyky, které nelze generovat nekontextovými gramatikami (kontextové gramatiky jsou tedy mohutnějším aparátem než gramatiky nekontextové, Chomsky 1959). Kontextová gramatika je výhodnější zejm. pro jazyky s pevným slovosledem. U jazyků se slovosledem volným vede k velkému počtu pravidel, což není výhodné, má-li být splněn požadavek jednoduchosti gramatiky.

Na obecném příkladě objasníme některé vlastnosti frázové gramatiky, které budou dále důležité při popisu transformační složky transformační gramatiky (spec. při zavedení transformačního pravidla). Příklad:

Slovník V : V_T = {a, b, c, d, e, f} V_N = {E, C, F, A, D}

Pravidla: S → EF; E → AC; F → Df; A → a; C → bc; D → de

Derivace D₁ terminálního řetězu abcdef:

               (S, EF, ACF, ACDf, aCDf, abcDf, abcdef)

Derivace D₂

               (S, EF, EDf, Edef, ACdef, aCdef, abcdef) atd.

Odvození terminálního řetězu není — jak zřejmo — jednoznačné. Mluvíme o ekvivalenci dvou derivací D_i a D_j, a to tehdy, jestliže je jimi odvozen stejný terminální řetěz se stejnou strukturou (znázorněnou stromem, např. [5]).

Množinu řetězů ekvivalentních derivací nazveme frázovým ukazatelem (Phrase-marker, P-marker). V našem případě je tedy frázový ukazatel

K = {S, EF, EDf, Edef, ACF, aCF, AbcF, abcF, ACDf, AbcDf, ACdef, Abcdef, aCDf, aCdef, abcDf, abcdef}

Frázový ukazatel K lze dobře znázornit v nekontextové gramatice pomocí grafu — stromu:

 

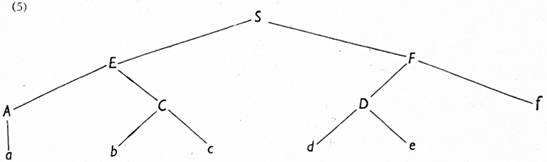
[144]Použijeme-li kontextové gramatiky, pak zavedením kontextového pravidla, např. a C F - a b c F (tedy C je možno přepsat pouze v kontextu a — F) dostaneme nový frázový ukazatel K':

K' = {S, EF, EDf, Edef, ACF, aCF, abcF, ACDf, ACdef, aCDf, aCdef, abcDf, abcdef} a jeho znázornění shodné s (5).

Znázornění obou fázových ukazatelů (K, K') stromem je tedy izomorfní, ačkoli se oba ukazatele sobě nerovnají. Proto je nutno k odlišení obou stromů zavést nějakou další relaci. Domníváme se, že touto relací může být po určité úpravě slovosledná relace, kterou pro nekontextové gramatiky zavedl K. Čulík (1963, § 2).

Frázová gramatika, jejíž aparát jsme zhruba popsali, má přispívat k tomu, aby bylo možno generovat všechny gramaticky správné věty přirozeného jazyka. V praxi se však ukázalo, že tento postup činí velké potíže (dokonce i v angličtině, která má slovosled daleko pevnější než čeština). Proto vznikla gramatika tranformační, která proti gramatice frázové obsahuje ještě složku transformační. Frázová složka transformační gramatiky se svým formálním aparátem v ničem neliší od výše popsané gramatiky frázové. Užívá se jí však pouze pro generování základních větných konstrukcí, jako je např. konstrukce subjekt + predikát + objekt (srov. ovšem doplnění na s. 145). K dalšímu rozvíjení takto získaných vět (tedy k tomu, co činilo ve frázové gramatice největší potíže) se pak užívá aparátu transformační složky.

 

Transformační složka. Základním jejím pojmem je transformační pravidlo. Obecně má tvar

(6)      φ → ψ,

kde φ, ψ jsou řetězy. Řetězem symbolů nahrazujeme opět nějaký řetěz, nikoli už, jak tomu bylo v gramatice frázové, jen jediný symbol. To nám dovoluje v transformační složce nahradit určitý řetěz jednoho frázového ukazatele řetězem jiného frázového ukazatele (např. aktivum můžeme nahradit pasívem: NP' + V + NP" → NP" + V (pas) + NP') nebo na základě dvou i více řetězů vytvořit další řetěz složitějsí (srov. přílohu, soupis 4), a to přímo, ne už postupným odvozováním jednotlivých symbolů.

Celý aparát transformační složky (TS') nezbytný k tomu, aby mohlo být transformačního pravidla užito, obsahuje podle Chomského tyto pojmy:

(7)      TS = [K, Z, Pr₁, Z', Pr₂],

kde K je frázový ukazatel, Z terminální řetěz základní, Z' terminální řetěz transformovaný, Pr₁ vlastní analýza (proper analysis) terminálního řetězu Z, Pr₂ vlastní analýza terminálního řetězu Z'.

Vysvětlíme ještě blíže pojem vlastní analýzy. Je to členění terminálního řetězu určené existencí tzv. strukturního indexu (structure index), jímž je kterýkoli z neterminálních řetězů frázového ukazatele. 

Např.	vlastní analýza	a	bc	de	f
	strukturní index	A	C	D	f

Existuje tu tedy např. relace D - de. Symbolu D odpovídá v terminálním řetězu segmentovaná část de (např. podmět - hezký dům; při generování vycházíme od pojmu podmětu a nahrazujeme ho konkrétním vyjádřením, které může být opět složené).[11]

Protože transformacemi odvozujeme nějaké nové věty přirozeného jazyka a chceme, aby s nimi bylo možno nakládat jako s větami získanými pomocí frázové složky (tj. chceme je např. znovu transformovat), je třeba, abychom při odvození dostali vedle transformované věty (terminálního řetězu Z') i její frázový ukazatel. K tomu je nezbytné, aby výsledný terminální řetěz byl také [145]segmentován (tj. aby měl vlastní analýzu Pr₂ i strukturní index). Proto se zavádí pojem elementární transformace (T_el). Jeho podstatu objasníme v následujícím příkladě.

Máme transformovat A C D f → D A C g f

T_el (A) = D; T_el (C) = A; T_el (D) = Cg; T_el (f) = f.

(Každé jednotce původního řetězu se přiřazuje jednotka řetězu transformovaného.)

Smysl transformačního pravidla je v tom, že symboly původního řetězu jsou buď přeskupovány (mění se jejich pořadí), nebo jsou mezi ně přidávány symboly nové anebo některé původní symboly chybějí. Z tohoto hlediska vztahu mezi řetězem původním a řetězem výsledným obsahuje transformační pravidlo jednak index uspořádání, jednak tzv. konstantní část.

Index uspořádání (term arrangement) určuje výsledné pořadí, kterého nabývají členy základního řetězu přecházející do řetězu transformovaného. Konstantní část (constant part) zahrnuje to, co je transformací do základního řetězu přidáno, popř. co je z něho ubráno, a to s označením místa. Příklad (srov. výše):

Index uspořádání	3  1  2  4
konstantní část	(2)  g  (4)[12]

Úplný exaktní popis transformační složky je obsažen v Chomského práci (Chomsky 1955), bohužel tiskem nevydané. Přesné definice pojmů, o nichž jsme hovořili, jsou tu příliš složité, takže jsme je zde nemohli ani stručně uvést.

2. Příklad transformačních pravidel v češtině. Podáváme generování dvou vět, z nichž jedna je větou jednoduchou, druhá souvětím.[13] Transformační pravidla, kterých užíváme, jsou sestavena pouze vzhledem k těmto větám a nepředstavují ovšem všechna pravidla transformační gramatiky češtiny. Dokonce se v ní ani v této podobě nemusí vyskytnout.

Předběžné poznámky. V příloze 2 jsou uvedena frázová pravidla. Pravidla generování jsou zapsána zkráceným postupem, a to dvěma typy závorek označujících potenciální a alternativní výskyt. Snažili jsme se, aby na nich bylo vidět, které symboly jsou nositeli dané gramatické kategorie. Proti jiným jazykům (zejména angličtině) bylo nutno zavést jednotlivé symboly pro gramatické kategorie nutné při vyjádření kongruence. Zavedli jsme také určité třídy symbolů (v našem případě slov) dovolující nám stanovit, zda určité transformace můžeme užít (srov. FT 2, kde užití transformace mimo jiné závisí právě na výskytu V₃ a V₅). V naší příloze je ovšem tento systém neúplný.

V popisu frázových pravidel je užito ještě jedné pravidelnosti, a to v etapě bezprostředně před použitím morfonologických pravidel (srov. dále). Zde označujeme symbolem začínajícím velkým písmenem kmen slova. Gramatické kategorie, které slovní tvar z tohoto kmene utvořený určují, označujeme malými písmeny a řadíme je za tento první symbol. Takový postup je výhodný pro určení konce slova i při užití morfonologických pravidel.

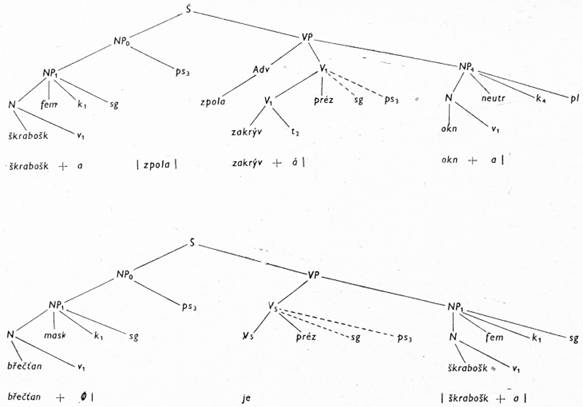
V procesu generování, který uvádíme, je vidět, že pouhým užitím frázových pravidel nedostaneme větu přirozeného jazyka (terminální řetěz), jak by mohlo vyplývat z našeho výkladu (srov. s. 144). Je třeba užít transformace. Toto minimum transformací, jichž je nezbytně třeba, aby bylo možno z řetězu získaného frázovou složkou dostat nejjednodušší — jaderné — věty (kernel sentences) přirozeného jazyka, nazval Chomsky obligatorními transformacemi (obligatory transformation), srov. příl. 3. V našem příkladě jsou obligatorní transformace nutné k přenesení kategorie osoby, čísla a rodu od subjektu k predikátu. Po odvození jaderných konstrukcí je možno odvozovat věty další. Toto odvozování se provádí fakultativními transformacemi (optional transformation), srov. příl. 4. (Název fakultativní je zde kladen do protikladu k termínu obligatorní v tom smyslu, že fakultativními transformacemi odvozujeme sice také terminální řetězy, jejich použití však není nevyhnutelné. Je třeba mít stále na mysli, že transformace jsou takto rozčleněny pouze z hlediska generování terminálního řetězu jaderné věty.) Jak naznačil i Chomsky (Chomsky 1961, s. 22, 23), je u obojího typu transformací (obligatorních i fakultativních) k sestavení transformovaného frázového ukazatele nezbytné zavést pro každé pravidlo generování zvlášť vyjádření všech relací generativní podřazenosti (o generativní podřazenosti srov. Čulík 1963), které při transformaci nově vznikají. Ve složitějších případech je někdy nutno doplnit i některý symbol (srov. FT 4). Je to řešení zajisté těžkopádné. Připomínáme, že vlastní podobu těchto [146]speciálních pravidel jsme volili jen vzhledem k našemu konkrétnímu příkladu, nikoli tedy s obecnou platností.

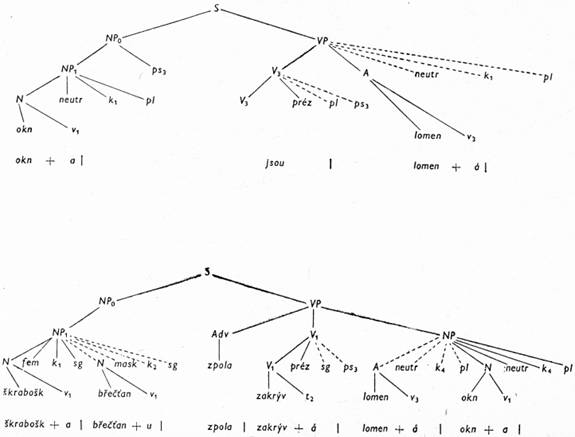
Poslední fáze odvození věty přirozeného jazyka se provádí morfonologickými pravidly (příl. 5). Podobně jako v transformačních pravidlech přepisuje se zde nějaký řetěz řetězem jiným: z konkrétního slova a gramatických kategorií se generuje slovní tvar.

Na závěr našeho stručného popisu podotýkáme, že některé problémy v transformační gramatice nejsou ještě vyjasněny. Týká se to především pravidel, kterými se odvozuje transformovaný frázový ukazatel, jehož struktura je zcela jiná než struktura původního frázového ukazatele, a konečně způsobu užití jednotlivých transformací, tj. přesné stanovení vzájemného pořadí, popř. libovůle atd. To jsou však otázky, které přesahují rámec našeho informativního sdělení.

Příloha: Podáváme ukázku pravidel transformační gramatiky nutných k odvození dvou vět: Škraboška břečťanu zpola zakrývá lomená okna. Konzervujíc aristotelovskou metafysiku, představovala wolfofská filosofie pokračování tradice scholastické filosofie. Uvádíme zde pouze ukázku generování první věty. Druhou větu může čtenář generovat podle pravidel zde uvedených sám. (Věta má tyto jaderné konstrukce: filosofie představovala NP₄; tradice pokračuje; filosofie konzervovala metafyziku, filosofie je wolfofská; filosofie je scholastická; metafysika je aristotelovská; filosofie má tradici).

1. Symbolika. (Uvedená vysvětlení symbolů mají pouze charakter pomocný, „neformální“; nejde tedy o interpretaci symbolů.) 

S	— symbol věty
NPi	— jmenná část v i-tém pádě (i = 1, .., 7)
Pronj	— osobní zájmeno j-té osoby (j = 1, 2, 3)
N	— jméno
VP	— slovesná část
Adv	— adverbium
Vn1, 2	— sloveso n-tého druhu (n = 1, 2, 3, 4, 5, …), horní indexy: 1 dokonavé sloveso, 2 nedokonavé sloveso
Aux	— pomocné sloveso
Partk	— kondicionální částice (bych, bys ..)
M	— modální sloveso
A	— adjektivum
C	— spojka; C(,)— spojka „čárka“
L	— označuje libovolný symbol začínající velkým písmenem
L'	— čárka nad písmenem označuje totožnost lexémů
X, Y, Z, W, Q — pomocné symboly označující libovolné řetězy, také nulové
psj	— kategorie osoby (j = 1, 2, 3)
gk	— kategorie rodu (k = mask, fem, neutr)
ki	— kategorie pádu (i = 1, .., 7)
nj	— kategorie čísla (j = sg, pl)
préz, min, fut — přítomný, minulý, budoucí čas
akt	— rod činný
inf	— infinitiv
t1	— slovesná třída (1, 2, ..)
v1	— vzor (1, 2, 3, …)
x	— řetěz symbolů zapsaných malými písmeny
{ }	— alternativní výskyt
( )	— potenciální výskyt
⊰	— relace generativní podřazenosti
/	— mezera
#	— hranice věty
„škraboška, metafysik“ — zde značí čárka alternativní výskyt

 

[147]2. Frázová pravidla (FP)

 

 

3. Obligatorní transformace (OT)

 

 

 

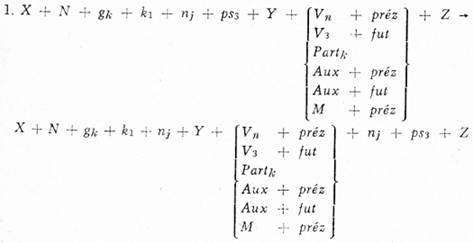
[148]Závislost v transformovaném fráz. ukazateli:	Vn ⊰ nj
	Vn ⊰ ps3

 

 

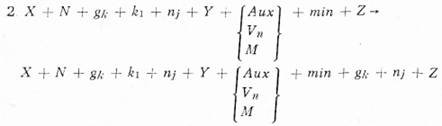
Závislost v transformovaném fráz. ukazateli:	Vn ⊰ gk
	Vn ⊰ nj

3. X + N + g_k + k₁ + n_j + Y + V₃ + Z + A₁ + W →

                     X + N + g_k + k₁ + n_j + Y + V₃ + Z + A + g_k + k₁ + n_j + W 

Závislost v transformovaném fráz. ukazateli:	VP ⊰ gk
	VP ⊰ k1
	VP ⊰ nj

4. X + L' + x + L" + Y → X + L' + x / L" + Y

 

4. Fakultativní transformace (FT)

1. X + NP'₁ + V₃ + A₁ + Y     → Z + A + g_k + k_i + n_j + N' +

    Z + N' + g'_k + k'_i +n'_i + W             + g'_k + k'_i + n'_j + W

Závislost v transformovaném fráz. ukazateli: L ⊰ A; L ⊰ g_k; L ⊰ k_i;

                            L ⊰ n_j; kde L je symbol, o němž platí L ⊰ N'

 

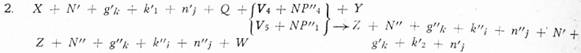
Závislost v transformovaném fráz. ukazateli: L ⊰ N'; L ⊰ g'; L ⊰ k'_i; L ⊰ n’_j;

kde L je symbol, o němž platí L ⊰ N"

 

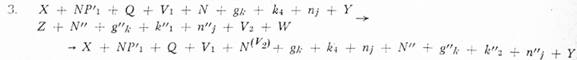
Závislost v transformovaném fráz. ukazateli: NP₄ ⊰ N; NP₄ ⊰ g_k; NP₄ ⊰ k₄;

                NP₄ ⊰ n_j; NP₄ ⊰ N"; NP₄ ⊰ g"_k; NP₄ ⊰ k"₂; NP₄ ⊰ n"_j;

 

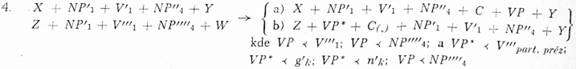
Závislost v transformovaném fráz. ukazateli:	a) S ⊰ C; S ⊰ VP
	b) S ⊰ VP*; S ⊰ C(,)

 

5. Morfonologická pravidla

 

 

[149]

 

[150]

 

[151]

 

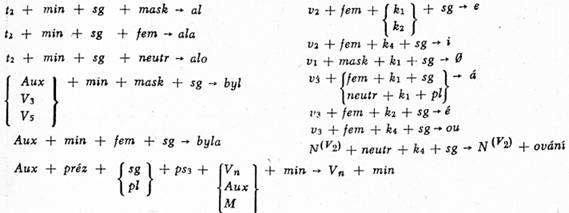
Poslední pravidlo: X + X → XX (tj. spojení kmenů a koncovek slov).

Slovo a slovesnost, volume 24 (1963), number 2, pp. 140-151

Previous Karel Berka, Pavel Novák: Výklad fonologických a gramatických pojmů pomocí pojmů teorie množin (Nad knihou I. I. Revzina Modeli jazyka, Moskva 1962)

Next Blanka Borovičková: Percepční identifikace samohláskových pozičních a stylistických variant