Relace a operace v syntaxi

Ladislav Nebeský, Petr Sgall

[Articles]

(pdf)

Реляция и операция в синтаксисе / La rélation et l’opération dans la syntaxe

V teoretické lingvistice se často vyšetřují binární i jiné relace mezi slovy, resp. mezi frázemi (řetězy slov), které nějakým způsobem souvisejí s vlastnostmi vět. Obvykle jde o některý z tří následujících případů, které se v lingvistice ne vždy dost jasně rozlišují:

1. Relace je definována na množině slov (resp. frází) daného jazyka a je závislá na množině vět jazyka jako celku. Sem patří relace ekvivalence (vzájemné zaměnitelnosti) frází (Bar-Hillel) nebo slov (Bar-Hillel, Kulagina).[1]

2. Relace je definována na množině těch slov (frází), která jsou částí dané věty; ke každé větě tedy existuje relace zvláštní.

3. Relace je definována na množině výskytů slov (frází) v dané větě. Sem patří relace závislosti větných členů. Tento případ někdy bývá nepřesně směšován s případem 2. Svádí k tomu to, že se často slova vyskytují ve větě jen jednou.

Vedle relací mezi slovy (frázemi) vyšetřují se v algebraické lingvistice i vlastnosti některých operací. Následující názorný příklad snad rozdílnost těchto pojmů podtrhne. Na množině celých čísel máme definovány různé binární operace, např. sčítání a násobení, a také různé binární relace, jako např relaci rovnosti (=) nebo nerovnosti (≠) mezi čísly. Formule 4 + 4 nebo 7 × 9, z nichž v každé se vyskytují symboly dvou čísel, je opět znakem pro nějaké číslo (v prvém případě pro číslo 8, v druhém pro číslo 63). Formule 4 = 4 nebo 7 ≠ 9 sice něco o dvojicích čísel vypovídají, ale samy znakem žádného čísla nejsou. To je charakteristický rozdíl mezi operací a relací. Jde jednak o operace definované na množině frází jazyka, jednak o operace definované na množině formulí nějakého syntaktického kalkulu jazyk popisujícího. Na množině frází jazyka lze definovat binární asociativní operaci zvanou obvykle sřetězení, která připisuje jednu frázi k druhé (sřetězení fráze dnes večer s frází bude pršet je fráze dnes večer bude pršet). Vzhledem k tomu, že jde o operaci jedinou a navíc asociativní, není třeba pro ni zavádět zvláštní symbol. Množina všech frází složených pouze ze slov jazyka je tedy množinou s jedinou binární asiciativní operací (volnou pologrupou). Jestliže nám jde o rozlišení více způsobů, jimiž se fráze (tedy i jednotlivá slova) spojují v nové fráze, vystupujeme již z úrovně jazyka, neboť pracujeme s frázemi (řetězy, formulemi), u nichž se kromě slov přirozeného jazyka vyskytují i jiné symboly. Dostáváme se tak na úroveň nějakého syntaktického kalkulu, tedy na úroveň nějaké teorie o jazyce.

U lingvistických autorů lze někdy najít nejistotu v užívání pojmů relace a operace. Nejzřetelněji je to vidět na tom, že vlastnosti relací (reflexívnost, symetričnost, tranzitivnost) se přisuzují operacím a naopak (nejčastěji se zaměňuje komutativnost se symetričností, někdy také idempotence s reflexívností, zřídka asociativnost s tranzitivitou). I když někde existují těsné souvislosti mezi relací a operací, např. mezi relací závislosti mezi výskyty slov ve větě (případ 3) a skládáním frází v nové fráze, směšování nebo krátká spojení mezi těmito pojmy vedou k teoretickým nejasnostem. Obsah našeho článku koresponduje s obsahem prvního paragrafu studie [219]S. K. Šaumjana,[2] zejména s jeho zavedením operace, kterou nazývá aplikací (a která — jak zdůrazňuje — je odlišná od operace sřetězení), a zavedením relace, kterou nazývá aplikativní dominací (její definiční obor není jasně vymezen — srov. naše body 1, 2, 3). Způsob, jímž od operace aplikace přechází k relaci dominace, se nám jeví jako „krátké spojení“. Naším cílem naproti tomu bylo projít obdobnou cestu od operace k relaci krok za krokem a nenechat žádný úsek nevyjasněn.

Také v některých našich pracích z teoretické lingvistiky zůstávají bez podrobného vyjasnění otázky týkající se vztahu mezi syntaktickými relacemi a operacemi užívanými v symbolickém zápisu větných struktur.[3] Bude tedy na místě probrat tyto vztahy pokud možno soustavně. Učiníme tak na příkladu relace závislosti v češtině.

Jak jsme se již zmínili, mezi tvořením frází a závislostní relací výskytů slov ve frázi existují jisté souvislosti. Zkonstruujeme zde jednoduchý syntaktický kalkul a ukážeme, jak od něho lze dojít k relaci závislosti.

Písmenem A označíme množinu slovních tvarů přirozeného jazyka. Jako R a R’ označíme dva funktory, pomocí nichž budeme z prvků množiny A tvořit formule. Množinu všech formulí uvažovaného syntaktického kalkulu — označíme ji K — budeme definovat induktivně:

1. Každý prvek množiny A je formule.

2. Jestliže x a y jsou formule, jsou také Rxy, R’xy formule.

3. Žádné další formule v jazyce nejsou.

Kalkul K však ještě sám přirozený jazyk popisovat nemůže; k tomu je třeba z množiny formulí vydělit její podmnožinu — označíme ji L; její prvky budeme nazývat přípustnými formulemi; přípustné formule budou takové formule, které popisují věty jazyka, a to způsobem odpovídajícím naší teorii.

Ukážeme to na příkladě. Předpokládejme, že A je množina slovních tvarů češtiny vystupujících jako větné členy. Potom do A patří mj.: malý, postiženému, ztracenou, chlapec, stokorunu, vrátil. Do množiny K patří např.: malý, stokorunu, vrátil, R chlapec stokorunu, R’ ztracenou postiženému, R’ chlapec, RR’ ztracenou chlapec chlapec, RR malý chlapec R’R’ vrátil postiženému R ztracenou stokorunu, R’R malý chlapec R vrátil R postiženému R ztracenou stokorunu, R’RR malý chlapec R vrátil postiženému R ztracenou stokorunu.

Z formulí, které jsme právě vyjmenovali, budou do množiny L patřit pouze tři formule: vrátil. RR malý chlapec R’R’ vrátil postiženému R ztracenou stokorunu, R’RR malý chlapec R’ vrátil postiženému R ztracenou stokorunu.

Pro každou formuli x ∊ K budeme definovat pojem podformule. Tato definice bude rovněž induktivní:

1. Formule x je podformulí formule x.

2. Jestliže u a v jsou formule a Ruv (resp. R’uv) je podformulí formule x, jsou formule u a v rovněž podformulemi formule x.

Tak např. formule (1) R’RR malý chlapec R’ vrátil postiženému R ztracenou stokorunu má kromě sebe samé tyto podformule:

RR malý chlapec R’ vrátil postiženému, R ztracenou stokorunu, R malý chlapec, R’ vrátil postiženému, malý, chlapec, vrátil, postiženému, ztracenou, stokorunu. For[220]mule RR malý chlapec R’ nesl R malý míč má kromě sama sebe tyto podformule: R’ nesl R malý míč, R malý míč, R malý chlapec, nesl, malý, chlapec, míč.

Má-li zápis věty v kalkulu K zachycovat strukturu věty z hlediska závislostní relace, musíme ovšem mít možnost na základě tohoto zápisu jednoznačně určit, který ze dvou výskytů v podformuli odpovídající syntaktické dvojici je „slovem řídícím“. Jak je z příkladů zřejmé, slouží nám k tomu právě rozlišení funktorů R a R’. Neformálně bychom mohli říci, že za řídící považujeme u funktoru R vždy druhý z jeho argumentů, kdežto u funktoru R’ vždy první. Pro formální zachycení této interpretace by bylo možné, jak se na první pohled zdá, definovat řídící slovní tvar podformule x [označený r (x)] takto:

1. Je-li x ∊ A, je r (x) = x.

2. Jsou-li x, y ∊ K, je r (Rxy) = r (y), r (R’xy) = r (x).

Tak např. pro formuli (1) by pak platilo, že řídícím slovem podformule R malý chlapec je slovní tvar chlapec, dále řídícím slovem podformule R’ vrátil postiženému je slovní tvar vrátil atd., jak to odpovídá dané koncepci (řídícím slovním tvarem celé věty je v tomto pojetí přísudek). Ale tak jednoduchá je situace jen díky tomu, že naše formule obsahuje jen výskyty slovních tvarů různých. Pro formule x = Raa, y = R’aa bychom podle uvedené definice dostali r(x) = r(y) = a, tzn. rozdíl mezi dvěma různými výskyty téhož slovního tvaru by nezůstal zachován, a to by vedlo k výsledkům jistě neuspokojivým.

Abychom mohli přímo pracovat ne s jednotlivými slovními tvary (jako s typy), ale s jejich výskyty, musíme použít postupu trochu složitějšího. Budeme pracovat s délkou formule x, označenou d(x), a s pořadovým číslem výskytu slovního tvaru; v dalším označujeme toto číslo n, příslušný výskyt p_n.

Jak již bylo řečeno, skládají se formule množiny K jednak ze slovoforem (z prvků množiny A), jednak ze symbolů R a R’. Nechť x ∊ K. Jako d(x), čili délku formule x, označíme počet výskytů slovoforem ve formuli x; jako p_n(x), kde n = 1, … d(x), označíme n-tý výskyt slovoformy ve formuli x.

Jestliže tedy jako x označíme formuli RR malý chlapec R’ nesl R malý míč, je d(x) = 5, p₁(x) = malý, p₂(x) = chlapec, p₃(x) = nesl, p₄(x) = malý, p₅(x) = míč.

Nechť x ∊ K. Jako r(x) označíme pořadové číslo toho výskytu slovoformy ve formuli x [tedy číslo z množiny 1, …, d(x)], které je definováno takto:

1. Je-li x ∊ A, je r(x) = 1.

2. Je-li x = Ruv, kde u a v jsou nějaké formule, je r(x) = d(u) + r(v).

2'. Je-li x = R'uv, kde u a v jsou nějaké formule, je r(x) = r(u).

Tak např. r (malý) = r (chlapec) = r (nesl) = r (míč) = 1;

r (R malý chlapec) = r (R malý míč) = 2;

r (R' nesl R malý míč) = 1; r (RR malý chlapec R' nesl R malý míč) = 3;

Podobně dostáváme, že r (RR malý chlapec R'R' vrátil postiženému R ztracenou stokorunu) = r (R'RR malý chlapec R' vrátil postiženému R ztracenou stokorunu) = 3.

Výskyt slovoformy ve formuli x s pořadovým číslem r(x) budeme nazývat řídící výskyt. Jak jsme viděli, řídící výskyt v nějaké formuli najdeme pomocí řídících výskytů v jejích podformulích.

Dalším pojmem, který zavedeme, bude určitá binární relace mezi pořadovými čísly výskytů slovních forem v nějaké formuli, tedy binární relace na množině 1, …, d(x), pro každé x ∊ K. Tato relace odpovídá relaci závis[221]losti výskytů slovních tvarů. I tentokrát budeme definovat induktivně a v definici využijeme pojmu řídícího výskytu.

Nechť x ∊ K. Jako Z_x (i, k), kde i, k = 1, …, d(x), označíme takový vztah mezi čísly i a k, který je ve formuli (x) splněn, právě když v dané formuli (x) existují podformule u a v takové, že x = Ruv nebo R'uv a nastane některá z těchto alternativ:

1. 1 ≤ i ≤ d(u), 1 ≤ k ≤ d(u), a platí Z_u(i, k)

2. d(u) < i ≤ d(x), d(u) < k ≤ d(x) a platí Z_v[i-d(u), k-d(u)]

3. 1 ≤ i ≤ d(u), d(u) < k ≤ d(x) x = Ruv, i = r(u), k = r(v) + d(u)

4. 1 ≤ k ≤ d(u), d(u) < i ≤ d(x), x = R'uv, k = r(u), i = r(v) + d(u).

Na první pohled je definice relace Z_x (i, k), x ∊ K trochu složitá. Předvedeme si ji na následujících třech příkladech. Struktura těchto případů je tato: tvar formule; pořadová čísla výskytů slovoforem; šipky, které spojují (ve směru i → k) právě ta pořadová čísla, která jsou v relaci.

(1) R'RR malý  chlapec  R'  vrátil  postiženému  R  ztracenou   stokorunu

               

(2) RR malý  chlapec  R'R'   vrátil   postiženému  R ztracenou  stokorunu

            

(3) RR malý   chlapec  R'  nesl  R  malý  míč

            

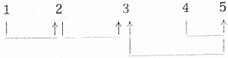
Od dvou binárních operací v jistém syntaktickém kalkulu došli jsme k binární relaci mezi výskyty slovních tvarů, které se v těchto formulích nacházejí (přesněji mezi jejich pořadovými čísly). Tuto relaci lze interpretovat jako závislostní relaci, tedy jako jistý rozbor fráze, která z formule vznikne, vypustíme-li z ní všechny výskyty symbolů R a R'.

Na množině K zavedeme další vztah. Řekněme, že formule x ∊ K a y ∊ K jsou si podobné, když

1. d(x) = d(y) = y

2. p₁(x) = p₁(y), …, p_n(x) = p_n(n)

3. Z_x(i, k) je právě, když je Z_y(i, k), pro všechna i, k = 1, …, n.

Je zřejmé, že formule (1) a (2) jsou si podobné. Řekněme, čím se liší: v (1) vytvářejí podformule R' vrátil postiženému a R malý chlapec spolu s funktorem R R podformuli RR malý chlapec R' vrátil postiženému, která pak spolu se zbývající podformulí R ztracenou stokorunu a funktorem R' vytváří celou formuli. V (2) je podformule R' vrátil postiženému spojena s podformulí R ztracenou stokorunu v podformuli R'R' vrátil postiženému R ztracenou stokorunu, a tato podformule pak spolu s podformulí R malý chlapec a funktorem R vytváří celou formuli.

To nás vede k následující definici. Nechť x ∊ K; 1 ≤ i, j, k ≤ d(x); Z_x(i, j), Z_x(j, k). Řekneme, že p_i(x) je ve formuli x těsněji spojeno s p_k(x) než p_j(x), když nastane jeden z těchto případů:

[222]1. Existují и, v ∊ K, takové, že x = Ruv a buď j ≤ d(u) < i, k nebo je d(u) < i, j, k, a současně p_{i — d (u)}(v) je ve formuli v těsněji spojeno s р_{k — d(u)}(v) než p_{j — d(v)}(v);

2. Existují u, v ∊ K, takové, že x = R'uv a buď i, k ≦ d(u) < j nebo je d(u) ≥ i, j, k a současně p_i(u) je ve formuli и těsněji spojeno s p_k(u) než р_j(u).

Ani tato definice není jednoduchá, i když vymezuje pojem na první pohled dosti názorný. Ale pojem, který je nám „jasný“ na několika příkladech, ztrácí obvykle názornost, chceme-li ho vymezit obecně.) Vrátíme se proto k příkladům. Formuli (1) si označíme x; vidíme, že platí Z_x (4, 3) a Z_x (6, 3). Ukážeme, že p₄(x), tj. čtvrtý výskyt slovního tvaru ve formuli s, je ve formuli x spojeno těsněji s p₃(x) než p₆(x). Formuli x lze psát ve tvaru x = R'uv, kde и = RR malý chlapec S vrátil postiženému, v = R ztracenou stokorunu; jak vidíme d(u) =4 a 4, 3 < 4 < 6; podmínky definice (případ 1) jsou splněny. Nyní si jako x označíme formuli (2). Ukážeme, že p₆(x) je ve formuli x spojeno těsněji s p₃(x). Formuli x lze psát ve tvaru x = Ruv, kde и = R malý chlapec, v = R'R' vrátil postiženému R ztracenou stokorunu. Vidíme, že d(u) = 2 < 3, 4, 6; náš předpoklad bude tedy splněn právě když p₆(x) = p₄(v), tj. šestý výskyt slovního tvaru ve formuli x, který je totožný s čtvrtým výskytem slovního tvaru ve formuli v, bude ve formuli v těsněji spojen s p₃(x) = p₁(v). Formuli v můžeme psát ve tvaru v = R'uv, kde и = R' vrátil postiženému, v = R ztracenou stokorunu. Vidíme, že 1, 2 < d(u) = 2 < 4. Tím je naše tvrzení ověřeno. Jak jsme ukázali na formulích (1) a (2), formule, které jsou si podobné, liší se právě různou těsností spojení výskytu slovních tvarů.

Každá formule x∊ K definuje jedinou frázi (řetěz) p₁(x) … p_n(x), kde n = d(x) a jedinou relaci Z_x, kterou lze interpretovat jako závislostní rozbor této fráze. Ovšem k jedné frázi a₁ … a_n а binární relaci na množině 1, …, n může naopak existovat formulí několik; podle naší definice jsou si všechny takové formule podobné, viz např. formule (1) a (2). S těmito formulemi není si ovšem podobná formule R'R' malý chlapec R vrátil R postiženému R ztracenou stokorunu, která definuje zcela jinou závislostní relaci (v daném případě lingvisticky nevhodnou).

Cesta od formule k frázi a relaci je jednoznačná; můžeme proto mluvit o relaci definované operací; v našem případě operace R a R' společně definují relaci Z_x. Opačná cesta, od fráze k formuli a od relace k operaci, jednoznačná není; jedné frázi odpovídají všechny formule, které jsou si navzájem podobné.

V zápisu formulí jsme používali tzv. bezzávorkové notace; tu je možno převést na obvyklejší notaci závorkovou, v níž bychom např. místo Ruv psali (uRv), místo R'uv — (uR'v).

Uvedenými změnami notace se tedy vztah mezi funktory R, R' а mezi relací Z_x i dalšími výše definovanými pojmy nemění. Kdybychom chtěli, aby frázi se závislostní relací odpovídala jednoznačně určitá formule, museli bychom volit kalkul jiný, kde by ovšem formulím z ∊ K navzájem si podobným odpovídala formule jediná.

 

R é s u m é

ОТНОШЕНИЕ И ОПЕРАЦИИ В СИНТАКСИСЕ

В статье указано, что лингвисты занимающиеся моделями языка в виде логических исчислений итп. нередко слишком коротким путем переходят от отношений (реляций) между языковыми единицами к операциям характерным для моделирующего исчисле[223]ния. В качестве примера исследуется отношение синтаксической зависимости и соответсвующие операции в исчисленении, определенном индуктивно:

1. каждый элементарный аргумент является формулой этого исчисления,

2. если х и у — формулы, то Rxy и R’xy также являются формулами.

Конечно, описанием синтаксической структуры языка является не это исчисление, а только какое-то подмножество его формул. При этом элементарные аргументы интерпретируются как лексикальные единицы. Далее определяется понятие определяемого (подчиняющего) слова — точнее: подчиняющего вхождения словоформы (короче говоря: из аргументов функтора R первый является подчиненным, второй подчиняющим; у функтора R’ первый аргумент — подчиняющий, второй — подчиненный). Оказывается, что отношения зависимости во фразе соответствующей данной формуле однозначно выводимы из операций типа R, R’. Но обратный путь (от отношения к операции) не является однозначным, т. к. фразе (с определенной структурой с точки зрения реляции зависимости) соответствует несколько формул, отличающихся т. наз. релятивной близостью некоторых из своих аргументов. Например формулы RaR’bc и R’Rabc соответствуют той же фразе  (в авторами принятой нотации).

Slovo a slovesnost, volume 26 (1965), number 3, pp. 218-223

Previous Karel Horálek: K teorii věty

Next Lubomír Doležel: Model stylistické složky jazykového kódování