Gramatické kategorie a „pojmy v situacích“

Miroslav Novotný

[Články]

(pdf)

Грамматические категории и «понятия в ситуациях» / Grammatical categories vs. concepts in situations

1. Úvod. R. Wille (1981, 1982) publikoval práci, v níž studoval, co je pojem, co je jeho extenze a intenze. Výsledkem jeho analýzy byla jistá algebraická struktura, kterou zde nazýváme situací; vycházeje z této struktury zavedl pojem v situaci, jeho extenzi a intenzi. V celém tomto článku pojmem rozumíme vždy Willeho pojem v situaci.

Willeho metody se však v algebraické lingvistice užívalo již dříve, viz např. práce J. Kunzeho (1967, 1968), M. Novotného (1981) a B. Kříže (1980, 1981). Autor se domnívá, že čtenáře-lingvistu může zajímat, jak se morfologické a syntaktické kategorie algebraické lingvistiky dají zavést v rámci obecné teorie pojmů v situaci.

Při výkladu budeme potřebovat standardní matematický aparát teorie množin, který lze částečně převzít z Chytilovy knihy (1984, s. 9—13). Připomeneme zde jen to, co v knize není, anebo je v ní zavedeno jinak než v tomto článku.

Buďte a, b jakékoliv prvky. Pak {a, b} je množina, tzv. dvojice, utvořená z prvků a, b. Vyznačíme-li jeden z těchto prvků, vznikne tzv. uspořádaná dvojice utvořená z těchto prvků; vyznačený prvek nazýváme jejím prvním členem, zbývající prvek jejím druhým členem. Uspořádaná dvojice s prvním členem a a s druhým členem b se značí symbolem (a, b). Jsou-li A, B množiny, pak A × B značí množinu všech uspořádaných dvojic (a, b) takových, že a ∈ A, b ∈ B. Je-li R ⊆ A × B, pak R se nazývá korespondence z množiny A do množiny B. Taková korespondence R se jmenuje zobrazení množiny A do B, jestliže ke každému a ∈ A existuje právě jedno b ∈ B tak, že (a, b) ∈ R. Pak místo (a, b) ∈ R píšeme také b = R(a). Zobrazení f množiny A do B se nazývá bijekce, má-li tyto dvě vlastnosti: (1.) Pro každé b ∈ B existuje a ∈ A tak, že f(a) = b. (2.) Pro každé a ∈ A a každé a' ∈ A s vlastností a ≠ a' platí f(a) ≠ f(b).

Buď I neprázdná množina, A zobrazení množiny I do nějaké množiny množin. Pro každé i ∈ I je tedy A(i) množina. Definujeme pak sjednocení množin A(i) jako množinu všech prvků, z nichž každý je aspoň v jedné množině A(i). Toto sjednocení značíme symbolem .

Nechť n je celé kladné číslo a V množina. Zobrazení a množiny {1, …, n} do V se nazývá uspořádaná n-tice prvků množiny V a značí se symbolem (a(1), …, a(n)) nebo a(1) … a(n) nebo také a₁ … a_n. Tuto definici lze rozšířit a definovat uspořádanou nultici prvků množiny V jako zobrazení množiny prázdné do V, což je ovšem prázdná množina. Uspořádanou nultici značíme symbolem Λ. Konečnou posloupností nebo též řetězem nad V rozumíme libovolnou uspořádanou n-tici prvků množiny V při jakémkoliv celém nezáporném čísle n.

Řetěz Λ se nazývá prázdný, řetěz, který dostaneme při volbě n = 1 (viz nahoře), se jmenuje jednočlenný. Místo , píšeme a^m.

Konec důkazu věty nebo konec příkladu označujeme symbolem □.

 

2. Pojmy, jejich intenze a extenze. Buďte dány dvě množiny G, M a korespondence r z množiny G do M. Pak uspořádanou trojici (G, M, r) nazveme situací. (Wille užívá názvu „kontext“; tento název si však rezervujeme pro něco jiného.) Prvky v množině G interpretujeme jako předměty, prvky v M jako příznaky; vztah (g, m) ∈ r značí, že předmět g má příznak m.

1. Příklad. Nechť je G = {Adamec, Bolek, Jirků, Nováková, Zeman}, M = {muž, žena, střední věk, vyšší věk, světlé vlasy, tmavé vlasy}. Korespondence r nechť je dána touto tabulkou:

 

[112]			Střední	Vyšší	Světlé	Tmavé
	Muž	Žena	věk	věk	vlasy	vlasy
Adamec	1	0	1	0	0	1
Bolek	1	0	0	1	1	0
Jirků	0	1	1	0	1	0
Nováková	0	1	1	0	0	1
Zeman	1	0	0	1	0	1

 

Zde jsme položili do průniku řádku začínajícího symbolem g a sloupce začínajícího symbolem m symbol 1, má-li předmět g příznak m; jinak je v tomto průniku 0. Tak lze např. z naší tabulky přečíst, že Adamec je muž středního věku s tmavými vlasy, Jirků žena středního věku se světlými vlasy atd. □

Buď dána situace (G, M, r). Pro každé X ⊆ G a každé Y ⊆ M klademe

s(X) = {m ∈ M; (g, m) ∈ r pro každé g ∈ X},

t(Y) = {g ∈ G; (g, m) ∈ r pro každé m ∈ Y},

p(X) = t(s(X)), q(Y) = s(t(Y)).

Uvedené definice mají tento význam: s(X) je množina všech příznaků, z nichž každý náleží všem předmětům množiny X; podobně je t(Y) množina všech předmětů, z nichž každý má všechny příznaky množiny Y.

2. Příklad. Buď (G, M, r) situace z příkladu 1, nechť X = {Adamec, Jirků}. Pak s(X) = {střední věk}. Položíme-li Y = {střední věk}, pak t(Y) = {Adamec, Jirků, Nováková}. Zejména je tedy p(X) = t(s(X)) = t(Y) = {Adamec, Jirků, Nováková}. Položme X₁ = {střední věk}. Tedy je zejména q(Y) = s(t(Y)) X s(X₁) = {střední věk}. □

Buď (G, M, r) situace. Pak pro každé X ⊆ G definujeme pojem vytvořený množinou předmětů X jako uspořádanou dvojici (p(X), s(X)). Podobně pro Y ⊆ M definujeme pojem vytvořený množinou příznaků Y jako uspořádanou dvojici (t(Y), q(Y)). Čistě matematickými prostředky lze dokázat, že (p(X), s(X)) = (t(s(X)), q(s(X))), (t(Y), q(Y)) = (p(t(Y)), s(t(Y))), takže pojem vytvořený množinou předmětů X je týž jako pojem vytvořený množinou příznaků s(X) a pojem vytvořený množinou příznaků Y je týž jako pojem vytvořený množinou předmětů t(Y). Lze tedy pojem definovat jako uspořádanou dvojici (E, I), kde E ⊆ G, I ⊆ M, s(E) = I, t(I) = E. Množinu E nazýváme extenzí pojmu (E, I), množinu I jeho intenzí.

3. Příklad. Pokračujeme-li v příkladě 2, zjistíme, že pro E = {Adamec, Jirků, Nováková}, I = {střední věk} tvoří uspořádaná dvojice (E, I) pojem s extenzí E a s intenzí I. Podobně zjistíme, že pro E₁ = {Adamec, Nováková}, I₁ = {střední věk, tmavé vlasy}, tvoří zase (E₁, I₁) pojem.

Volme nyní X = {Bolek, Nováková}. Pak s(X) = ∅ a tedy p(X) = t(s(X)) = t(∅) = {g ∈ G; (g, m) ∈ r pro každé m ∈ ∅}. Protože podmínce m ∈ ∅ nevyhovuje žádné m ∈ M, podmínka „(g, m) ∈ r pro každé m ∈ ∅“ je splněna pro každé g ∈ G. Tedy p(X) = G a množina X vytváří pojem (G, ∅) s prázdnou intenzí.

Z tohoto příkladu je vidět, že „člověk středního věku s tmavými vlasy“ je v naší situaci totéž jako množina {Adamec, Nováková}, neboť tato množina je extenzí pojmu, jehož intenzí je {střední věk, tmavé vlasy}. Dále je odtud vidět, že ne každá množina předmětů je extenzí nějakého pojmu, a podobně, ne každá množina příznaků je intenzí nějakého pojmu. Definice pojmu se dá slovy vyjádřit takto: Je to [113]uspořádaná dvojice (E, I), kde E se skládá z předmětů a I z příznaků; přitom I je množina všech příznaků, z nichž každý přísluší všem předmětům z množiny E a E je množina všech předmětů, z nichž každý má všechny příznaky z množiny I. □

Uvedené konstrukce byly inspirovány praktickými problémy. Wille uvádí jako jeden ze zdrojů inspirace Německý úřad pro normování (Deutsches Institut für Normung). Willeho metodou je ke každému pojmu v situaci jednoduše přiřazena jeho extenze a intenze. Tím se zřejmě vychází vstříc potřebám normující instituce.

 

3. Morfologické kategorie. Uvedené konstrukce se používalo v algebraické lingvistice již dříve, než Wille uveřejnil svůj článek (1981). Pokud je autorovi známo, první článek o algebraické lingvistice, v němž se tato konstrukce objevila, pochází od J. Kunzeho (1967, 1968).

J. Kunze ve svém článku definuje morfologické kategorie. V tradiční lingvistice byly již dávno — jak známo — definovány konkrétní morfologické kategorie. První definice morfologických kategorií v algebraické lingvistice formuloval R. S. Dobrušin (1957, 1961), příspěvky k tomuto tématu podal zejména S. Marcus (1962, 1965). Jejich definice vedly J. Kunzeho k nové definici, kterou dále zformulujeme. Napřed je však třeba říci, co se zde bude rozumět jazykem.

Buď dána nějaká neprázdná množina V. Utvoříme množinu všech řetězů nad V a označíme ji symbolem V*. Jednočlenné řetězy nad V neodlišujeme od prvků množiny V, takže máme V ⊆ V*. Mezi řetězy je definována operace sřetězení, a to takto: Buďte x, y řetězy nad V. Klademe xy = x = yx, je-li y = Λ. Je-li x = a₁ … a_m, y = b₁ … b_n, kde m ≧ 1, n ≧ 1 jsou celá čísla a a₁, …, a_m, b₁, …, b_n jsou prvky množiny V, klademe xy = c₁ … c_m+n, c_i = a_i pro každé i s vlastností 1 ≦ i ≦ m a c_i = b_i—m pro každé i s vlastností m + 1 ≦ i ≦ m + n. Analogickým způsobem se definuje sřetězení p řetězů při libovolném celém p s vlastností p ≧ 2. Řetěz y se nazývá podřetěz řetězu x, existují-li řetězy u, v tak, že x = uyv.

Operaci sřetězení přenášíme i na množiny řetězů. Je-li n ≧ 2 celé a A₁, …, A_n jsou podmnožiny množiny V*, klademe A₁ … A_n = {a₁ … a_n; a₁ ∈ A₁, …, a_n ∈ A_n}.

Jazykem (nebo též formálním jazykem) rozumíme uspořádanou dvojici (V, L), kde L ⊆ V* a V je konečná neprázdná množina.

V lingvistice interpretujeme prvky množiny V jako slovní tvary. Prvky množiny V* jsou tedy všechny možné řetězy slovních tvarů; množina L se skládá z takových řetězů, které odpovídají správným větám.

Jazyk (V, L) se nazývá netriviální, je-li L neprázdná množina.

1. Příklad. Je-li V množina všech českých slovních tvarů, je DĚTI ∈ V, ALE ∈ V; zde ovšem DĚTI považujeme za jediný symbol, podobně je ALE jediný symbol. Na druhé straně ALLE ∉ V, BRLSW ∉ V. Buď L množina všech správných českých vět. Pak je např. DĚTI PIJÍ ∈ L, DĚTI PIJÍ MLÉKO ∈ L, DĚTEM PIJÍ ∉ L, NA ALE U KDYŽ ∉ L, ačkoliv DĚTEM PIJÍ ∈ V*, NA ALE U KDYŽ ∈ V*.

V tomto příkladě i v dalších chápeme český jazyk (nebo jeho fragment) jako jazyk formální. Je třeba si přitom uvědomit, že je nutno zapomenout na mnoho informací, které o češtině máme: Užíváme jen znalostí o tom, co je a co není český slovní tvar, a co je a co není správná česká věta. Množinu všech českých slovních tvarů a množinu všech českých vět považujeme za danou; nezabýváme se tedy otázkou, jak se pozná správná česká věta. Zejména nám scházejí informace o významu slovních tvarů a vět. Zacházíme tedy s češtinou podobně jako badatel, který zkoumá neznámý jazyk v neznámém písmu. Má k dispozici seznam symbolů pro slovní tvary a z psaného materiálu získává řetězy těchto symbolů, o nichž ví, že odpovídají správným větám. Z těchto zdánlivě slabých prostředků se pokouší konstruovat morfologické kategorie, syntaktické kategorie a gramatiku jazyka. V příkladech [114]z češtiny budeme mít ovšem možnost konfrontovat formálně definované morfologické kategorie s tradičními a ukázat, jak je formální definice inspirována definicí tradiční.

Je-li (V, L) jazyk, pak libovolný prvek (u, v) ∈ V* × V* nazýváme kontextem nad V. Říkáme, že řetěz x ∈ V* je přijat kontextem (u, v), platí-li uxv ∈ L. Kontext (Λ, Λ) nazýváme triviální, ostatní kontexty netriviální.

2. Příklad. Buď (V, L) týž jazyk jako v příkladě 1. Položme u = NAŠE DĚTI, v = DOBRÉ MLÉKO, x = RÁDY PIJÍ, y = VIDÍ, z = NESE. Pak kontext (u, v) přijímá řetězy x, y, ale nepřijímá řetěz z. □

Položme nyní G₀ = V, M = V* × V*; pro libovolné a ∈ V, (u, v) ∈ V* × V* položme (a, (u, v)) ∈ r, právě když kontext (u, v) přijímá (jednočlenný) řetěz a, tj. právě když uav ∈ L. Pak (G₀, M, r) = (V, V* × V*, r) je situace ve smyslu odst. 2. Lze tedy nyní zopakovat konstrukce z odst. 2.

Pro libovolné X ⊆ V a libovolné Y ⊆ V* × V* máme tedy

s(X) = {(u, v) ∈ V* × V*; uav ∈ L pro každé a ∈ X},

t(Y) = {a ∈ V; uav ∈ L pro každé (u, v) ∈ Y},

p(X) = t(s(X)), q(Y) = s(t(Y)).

Pak množina p(X) se nazývá morfologická kategorie ve smyslu Kunzově vytvořená množinou X. Abychom tyto morfologické kategorie odlišili od morfologických kategorií tradiční gramatiky, budeme je nazývat morfologickými kategoriemi, zatímco pro morfologické kategorie tradiční gramatiky vyhradíme název tradičních morfologických kategorií.

Podle definice se tedy morfologická kategorie vytvořená množinou X slovních tvarů dostane tak, že se najdou všechny kontexty, z nichž každý přijímá všechny slovní tvary množiny X. Pak se najde množina všech slovních tvarů, z nichž každý je přijat všemi sestrojenými kontexty; poslední množina slovních tvarů je morfologická kategorie vytvořená množinou X.

Je-li tedy X ⊆ V libovolná množina, je (p(X), s(X)) pojem ve smyslu Willeho, jehož extenzí je morfologická kategorie p(X); intenzí je pak množina s(X) všech kontextů, z nichž každý přijímá všechny prvky z množiny X (a ovšem také z množiny p(X)). Prvky množiny s(X) lze také považovat za gramatické funkce, z nichž každou zastává libovolný prvek z množiny X.

3. Příklad. Položme X = {PÁNA, HRADU}. Uvažujme o kontextech (STAVÍM SE VEDLE, Λ), (VIDÍM, Λ), (STAVÍM SE PROTI, Λ). První z těchto kontextů přijímá oba slovní tvary z množiny X; druhý přijímá slovní tvar PÁNA, ale nepřijímá slovní tvar HRADU, třetí přijímá slovní tvar HRADU, ale nepřijímá slovní tvar PÁNA. Zřejmě tedy (STAVÍM SE VEDLE, Λ) ∈ s(X), (VIDÍM, Λ) ∉ s(X), (STAVÍM SE PROTI, Λ) ∉ s(X). Je-li tedy t ∈ p(X), pak t je slovní tvar přijatý kontextem (STAVÍM SE VEDLE, V). V úvahu tedy přicházejí např. slovní tvary ORÁČE, MEČE, KAMENE, LOKTE, ŽENY, PÍSNĚ, PANÍ, MĚSTA, MOŘE, STAVENÍ, KUŘETE, PÁNŮ, HRADŮ. Dále je vidět, že také (STAVÍM SE VEDLE MALÉHO, Λ) ∈ s(X). Z uvedených slovních tvarů jsou tímto kontextem přijaty jen slovní tvary PÁNA, HRADU, ORÁČE, MEČE, KAMENE, LOKTE, MĚSTA, MOŘE, STAVENÍ, KUŘETE. Předpokládáme, že množina L se skládá ze všech správných českých vět, jednoduchých i souvětí. Potom (STAVÍM SE VEDLE, KTERÝ STOJÍ) ∈ s(X). Z uvedené množiny slovních tvarů jsou tímto kontextem přijaty jen slovní tvary PÁNA, HRADU, ORÁČE, MEČE, KAMENE, LOKTE. Morfologická kategorie vytvořená množinou X je tedy tradiční morfologická kategorie podstatných jmen rodu mužského v 2. pádě jednotného čísla. □

4. Příklad. Buď nyní V množina všech českých slovních tvarů, L množina [115]všech českých jednoduchých vět, z nichž každá obsahuje přesně jeden slovní tvar slovesný a přesně jeden, který je podstatným jménem. Položme X = {PÁN, VIDÍME}. Pak s({PÁN}) ∩ s({VIDÍME}) = ∅. Vskutku, nechť (u, v) ∈ s({PÁN}). Pak u PÁN v ∈ L je řetěz, který obsahuje přesně jeden slovesný tvar. Tento slovesný tvar je tedy obsažen jako symbol v řetězu u nebo v řetězu v; tyto řetězy jsou složeny ze slovních tvarů. Pak ovšem řetěz u VIDÍME v obsahuje dva slovní tvary slovesné, a tedy podle naší definice nenáleží do L. Ze vztahu s({PÁN}) ∩ s({VIDÍME}) = ∅ snadno plyne s({PÁN, VIDÍME}) = ∅ a odtud podobně jako v příkladě 3, odst. 2 dostaneme p({PÁN, VIDÍME}) = t(s({PÁN, VIDÍME})) = t(∅) = V. Vidíme tedy, že v našem jazyce (V, L) je množina V všech slovních tvarů morfologickou kategorií. □

Z příkladů 3 a 4 je vidět, že existují morfologické kategorie, které jsou rovny tradičním morfologickým kategoriím, i morfologické kategorie, které mezi tradičními morfologickými kategoriemi nenajdeme. Nebudeme se zde zabývat otázkou, zda je každá tradiční morfologická kategorie zároveň morfologickou kategorií ve smyslu naší konstrukce. Teoreticky lze tuto otázku rozřešit takto: Buď X množina všech slovních tvarů, které tvoří tradiční morfologickou kategorii. Sestrojíme množinu p(X) způsobem, který byl v tomto odstavci popsán. Matematickými prostředky lze dokázat (srov. Birkhoff, 1948, kap. IV; Szász, 1963, s. 68—72): Je-li X = p(X), je tradiční morfologická kategorie zároveň morfologickou kategorií v našem slova smyslu; je-li X ≠ p(X), pak jí není.

Užitím této konstrukce J. Kunze (1967, 1968) studoval morfologické kategorie podstatných jmen v němčině.

 

4. Syntaktické kategorie. Syntaktické kategorie se liší z hlediska algebraické lingvistiky od kategorií morfologických hlavně tím, že jsou to množiny řetězů slovních tvarů, zatímco morfologické kategorie jsou množiny slovních tvarů. Syntaktické kategorie lze sestrojovat pomocí kontextů podobně jako kategorie morfologické. Definici syntaktické kategorie lze formulovat takto:

Buď (V, L) jazyk. Položme G = V*, M = V* × V*; pro x ∈ V*, (u, v) ∈ V* × V* položíme (x, (u, v)) ∈ R, právě když uxv ∈ L. Pak (G, M, R) je situace ve smyslu odst. 2. Lze tedy položit pro každé X ⊆ V* a každé Y ⊆ V* × V*:

S(X) = {(u, v) ∈ V* × V*; uxv ∈ L pro každé x ∈ X},

T(Y) = {x ∈ V*; uxv ∈ L pro každé (u, v) ∈ Y},

P(X) = T(S(X)), Q(Y) = S(T(Y)).

Pak P(X) se nazývá syntaktická kategorie vytvořená množinou řetězů X. Tato konstrukce se objevuje v Křížových pracích (1980, 1981), srov. též autorovu práci (1981).

Abychom tyto syntaktické kategorie odlišili od syntaktických kategorií tradiční gramatiky, budeme syntaktické kategorie tradiční gramatiky nazývat tradičními syntaktickými kategoriemi.

Je-li X ⊆ V* libovolná množina, je (P(X), S(X)) pojem ve smyslu Willeho, jehož extenzí je syntaktická kategorie P(X); intenzí je množina S(X) všech kontextů, z nichž každý přijímá všechny řetězy z množiny X (a ovšem také z množiny P(X)).

Při konstrukci příkladů nám pomůže tato věta, jejíž důkaz plyne ze známých výsledků teorie svazů (srov. Birkhoff, 1948, kap. IV; Szász, 1963, s. 68—72).

1. Věta. Buď (V, L) jazyk, (u, v) libovolný kontext nad V. Pak množina T({(u, v)}) je syntaktická kategorie a je rovna množině {x ∈ V*; uxv ∈ L}. □

Pro zkrácení klademe {x ∈ V*; uxv ∈ L} = L_{(u, v)} a množinu L_{(u, v)} nazýváme derivativem množiny L podle kontextu (u, v).

[116]2. Příklad. (a) Buď (V, L) jazyk, kde V je množina všech českých slovních tvarů a L je množina všech českých jednoduchých vět oznamovacích. Nechť (u, v) = (Λ, STOJÍM). Pak množina L_{(u, v)}, která je podle 1 syntaktickou kategorií, obsahuje řetězy Λ, JÁ, JÁ SÁM, JÁ SAMA atd., které náleží do tradiční syntaktické kategorie podmětu. Dále je ovšem i JÁ ČASTO ∈ L_{(u, v)}. Tedy se syntaktická kategorie L_{(u, v)} nerovná tradiční syntaktické kategorii podmětu.

(b) Nechť (V, L) je týž jazyk jako v (a). Volme X = {NESU, JSEM NESL}. Pak máme (JÁ, Λ) ∈ S(X), (JÁ SÁM, Λ) ∈ S(X), (JÁ, KNIHU) ∈ S(X), (JÁ, PĚKNOU KNIHU) ∈ S(X). Patrně každý kontext přijímající řetězy NESU, JSEM NESL přijme i řetězy PŘINESU, BERU, PÍŠI, JSEM NAPSAL, PÍŠI DOPIS atd.

Zdá se, že naše množina P(X) se v termínech tradiční gramatiky dá vyjádřit jako přísudek, který je vyjádřen přechodným slovesem v 1. osobě jednotného čísla s možnými dalšími rozvíjejícími členy; pokud toto sloveso vyjadřuje rod, jde o rod mužský. Rozhodnout, zde je tomu opravdu tak, není snadné. Důvodem je, že není lehké přehlédnout množinu S(X) všech kontextů přijímajících slovní tvary množiny X; tím těžší je pak najít množinu všech řetězů přijatých všemi kontexty množiny S(X). □

Tyto příklady ukazují, že právě zavedené syntaktické kategorie jsou z tradičního hlediska nezvyklé. Vzniká tedy přirozená otázka, jsou-li vůbec užitečné. Ukážeme, jak se s pomocí syntaktických kategorií dá sestrojit zobecněná gramatika každého jazyka.

 

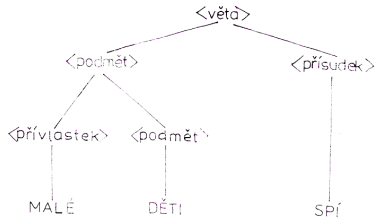
5. Zobecněné gramatiky. Tradiční gramatika přiřazuje ke každé větě její frázový ukazatel. Omezme se v dalším výkladu na jednoduché věty oznamovací, a to na věty dvojčlenné. Uveďme příklad takové věty a jejího frázového ukazatele:

Tento frázový ukazatel popisuje některé zákonitosti češtiny: (dvoučlenná jednoduchá) věta se skládá z jednoho spojení podmětu s přísudkem, podmět vyjádřený podstatným jménem rozvíjí ve větě přívlastek. Frázový ukazatel zároveň dává návod, jak lze větu formálně odvodit: Symbol <věta> nahradíme řetězem symbolů <podmět> <přísudek>, symbol <podmět> řetězem <přívlastek> <podmět>. Nakonec symboly <přívlastek>, <podmět>, <přísudek> nahradíme po řadě slovními tvary MALÉ, DĚTI, SPÍ. Tyto náhrady lze zapsat symbolicky jako pravidla:

<věta> → <podmět> <přísudek>, <podmět> → <přívlastek> <podmět>, <přívlastek> → MALÉ, <podmět> → DĚTI, <přísudek> → SPÍ. Snadno se nahlédne, že podobně utvořená věta MILÉ DĚTI SPÍ vede na jedno nové pravidlo: (přívlastek → MILÉ.

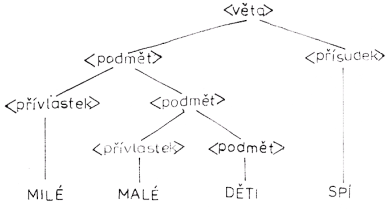
[117]Užitím těchto pravidel můžeme odvodit např. větu

Zároveň pozorujeme tuto skutečnost: Vyjdeme-li z libovolného symbolu syntaktické kategorie, je z něho odvozen jistý řetěz slovních tvarů, který náleží k této syntaktické kategorii. Tak např. v posledním příkladě je symbol <podmět> třikrát; v jednom případě je z něho odvozen (jednočlenný) řetěz DĚTI, v druhém MALÉ DĚTI, v třetím MILÉ MALÉ DĚTI. Všechny tři jsou schopny stát se podměty ve správných větách; poslední řetěz je podmětem ve větě z našeho posledního příkladu, druhý ve větě z prvního příkladu, první je podmětem v odpovídající holé větě.

Z těchto pozorování je vidět, že každá věta jazyka je určena jistou konečnou množinou jeho syntaktických kategorií, mezi nimiž je jedna vyznačena (zde je to kategorie se symbolem <věta>); dále je věta určena konečnou množinou slovních tvarů a konečnou množinou pravidel. Každé pravidlo je v našem pojetí uspořádaná dvojice řetězů utvořených ze symbolů syntaktických kategorií a ze slovních tvarů. Přitom první člen každé dvojice obsahuje aspoň jeden symbol syntaktické kategorie.

K určení všech vět jazyka (nebo jeho fragmentu) uvedeným způsobem je tedy potřeba zadat nějakou množinu jeho syntaktických kategorií a vyznačit jednu z nich, dále množinu slovních tvarů jazyka a množinu pravidel, která mají tvar, jaký jsme právě popsali.

Lze tedy zobecněnou gramatiku zformalizovat jako uspořádanou čtveřici G = (S, V, R, s₀), kde S, V jsou množiny bez společných prvků a V je konečná; dále je R ⊆ (S ∪ V)* S(S ∪ V)* × (S ∪ V)* a s₀ ∈ S. Prvky množiny S se nazývají neterminální symboly, prvky množiny V terminální symboly. Prvky v R se jmenují pravidla; jsou to uspořádané dvojice řetězů utvořených z terminálních i neterminálních symbolů. Je-li (y, x) ∈ R, nazýváme y levou a x pravou stranou pravidla (y, x).

V našich dosavadních úvahách byly prvky množiny V interpretovány jako slovní tvary, prvky množiny S jako symboly syntaktických kategorií. Aplikovat pravidlo na nějaký řetěz znamenalo najít v tomto řetězu podřetěz rovný levé straně pravidla a nahradit jej pravou stranou pravidla. To se formalizuje takto: Říkáme, že řetěz t ∈ (S ∪ V)* je přímo odvozen z řetězu s ∈ (S ∪ V)* pomocí pravidel z množiny R, a píšeme s ⇒ t (R), existují-li řetězy u ∈ (S ∪ V)*, v ∈ (S ∪ V)* a pravidlo (y, x) ∈ R tak, že s = uyv, uxv = t. V našich příkladech bylo dále vidět, že se pravidla postupně aplikují víckrát. To lze formálně vyjádřit takto: Říkáme, že řetěz t ∈ (S ∪ V)* je odvozen z řetězu s ∈ (S ∪ V)* pomocí pravidel z množiny R, a píšeme s  t(R), je-li buď s = t nebo existuje n ≥ 1 celé a řetězy t₀, t₁, …, t_n v množině (S ∪ V)* tak, že s = t₀, t_n = t a t_i—1 ⇒ t_i (R) pro 1, 2, …, n. Konečně klademe L(G) = {w ∈ V*; s₀  w (R)} a jazyk (V, L(G)) nazýváme jazykem generovaným zobecněnou gramatikou G = (S, V, R, s₀).

Ilustrujme si to na příkladě.

[118]1. Příklad. Položme S = {<věta>, <podmět>, <přísudek>, <přívlastek>}, V = {DĚTI, LEŽÍ, STOJÍ, MILÉ, MALÉ, HODNÉ}, R = {(<věta>, <podmět> <přísudek>), (<podmět>, <přívlastek> <podmět>), (<podmět>, DĚTI), (<přísudek>, LEŽÍ), (<přísudek>, STOJÍ), (<přívlastek>, MILÉ), (<přívlastek>, MALÉ), (<přívlastek>, HODNÉ)}, s₀ = <věta>. Pak G = (S, V, R, s₀) je zobecněná gramatika a platí např. (vynecháváme symbol (R)): <věta> ⇒ <podmět> <přísudek> ⇒ <přívlastek> <podmět> <přísudek> ⇒ <přívlastek> <přívlastek> <podmět> <přísudek> ⇒ MILÉ <přívlastek> <podmět> <přísudek> ⇒ MILÉ MALÉ <podmět> <přísudek> ⇒ MILÉ MALÉ DĚTI <přísudek> ⇒ MILÉ MALÉ DĚTI LEŽÍ a poslední řetěz je v množině V*. Tedy je tento řetěz v množině L(G). □

 

6. Konstrukce zobecněných gramatik pomocí syntaktických kategorií. V minulém příkladě jsme sestrojili zobecněnou gramatiku generující jistý velmi malý fragment češtiny. Úlohu neterminálních symbolů hrály symboly syntaktických kategorií v tradičním slova smyslu.

Pokus sestrojit podobnou zobecněnou gramatiku generující celý český jazyk naráží především na potíž, že tradiční syntaktické kategorie nejsou vhodné pro zavedení neterminálních symbolů. Tak např. pravidlo (<věta>, <podmět> <přísudek>) by znamenalo, že libovolný řetěz slovních tvarů odvozený ze symbolu <podmět> by se dal kombinovat s libovolným řetězem slovních tvarů odvozeným ze symbolu <přísudek>; tedy, jinak řečeno, podmět libovolné věty doplněný přísudkem libovolné jiné věty by měl dávat správnou větu. To jistě není pravda. Východisko lze najít v tom, že nezavedeme tradiční syntaktické kategorie, nýbrž syntaktické kategorie definované v odst. 4. Konstrukce zobecněné gramatiky založené na těchto kategoriích má tu výhodu, že ji lze aplikovat na jakýkoliv jazyk, že se tedy neomezuje jen na jazyky přirozené. Tuto konstrukci dále popíšeme.

Buď (V, L) netriviální jazyk, C neprázdná množina netriviálních kontextů nad V. Zavedeme nyní množinu P takto:

(1) L ∈ P. (2) Je-li Q ∈ P, (u, v) ∈ C a Q_{(u, v)} ≠ ∅, je Q_{(u, v)} ∈ P.

To tedy značí, že do množiny P náleží množina L, dále všechny neprázdné derivativy množiny L podle kontextů z množiny C, dále neprázdné derivativy těchto derivativů podle kontextů množiny C atd. Snadno se dokáže, že všechny prvky množiny P lze vyjádřit jako neprázdné derivativy množiny L podle jistých kontextů složených z kontextů množiny C, takže prvky množiny P jsou neprázdné syntaktické kategorie jazyka (V, L).

Dále klademe

r₁ = {(Q, uQ_{(u, v)}v); Q ∈ P, (u, v) ∈ C, Q_{(u, v)} ∈ P}.

Tvoříme tedy množinu uspořádaných dvojic; na prvním místě je vždy prvek množiny P, na druhém řetěz utvořený z prvků množiny P ∪ V. Tyto dvojice bychom mohli považovat za pravidla s neterminálními symboly v množině P a s terminálními v množině V, kdyby množiny P a V neměly společných prvků; to ovšem nemáme zaručeno. Proto raději neterminální symboly budeme brát z nové množiny S, která má stejný počet prvků jako P a která je disjunktní s množinou V. Nechť je dána bijekce přiřazující k libovolnému Q ∈ P prvek Q̅ ∈ S. Položíme proto

R₁ = {(Q̅, uQ̅_{(u, v)}v); Q ∈ P, (u, v) ∈ C, Q_{(u, v)} ∈ P}.

tato množina se dá považovat za množinu pravidel s neterminálními symboly z množiny S a s terminálními symboly z množiny V. Podobně definujeme

R2 = {(Q̅, t); Q ∈ P, t ∈ Q —		{u} Q(u, v){v}}.

[119]Také prvky v množině R₂ jsou pravidla. Na levé straně každého pravidla je symbol Q̅ odpovídající nějakému prvku Q z množiny P, na pravé straně je řetěz z množiny Q, který nelze ze symbolu Q přímo získat pomocí žádného pravidla z množiny r₁, tedy řetěz, který nelze napsat ve tvaru uxv při žádném (u, v) ∈ C a žádném x ∈ V*. Položme nakonec

G(V, L, C) = (S, V, R₁ ∪ R₂, L).

Pak G(V, L, C) je zobecněná gramatika, která má tyto vlastnosti:

1. Věta. Buď (V, L) netriviální jazyk, C neprázdná množina netriviálních kontextů nad V. Pak má zobecněná gramatika G(V, L, C) = (S, V, R₁ ∪ R₂, L) tyto vlastnosti:

(i) Pro každé Q ∈ P a každé w ∈ V* platí w ∈ Q, právě když Q̅  w (R₁ ∪ R₂).

(ii) G (V, L, C) generuje (V, L).

Důkaz této věty lze najít u Kříže (1980, 1981). □

Věta má tento smysl: Z každého neterminálního symbolu je odvozena pomocí pravidel zobecněné gramatiky množina řetězů, která je syntaktickou kategorií výchozího jazyka; to je vlastnost, kterou jsme pozorovali na motivačních příkladech.

Předvedeme nyní konstrukci zobecněné gramatiky G(V, L, C) na příkladě. V odstavci 4 jsme viděli, že je poměrně nesnadné konstruovat syntaktické kategorie pro přirozené jazyky nebo jejich fragmenty. Proto se naše ilustrace nebude týkat přirozeného jazyka.

2. Příklad. Buď V = {a, b}, L = {a^mba^m; m ≥ 0} ∪ {ab^ma; m ≥ 0}, C = {(a, a), (A, b)}. Položme Q = L_{(a, a)} = {a^mba^m; m ≥ 0} ∪ {b^m; m ≥ 0}, N = L_{(Λ, b)} = {Λ}, M = Q_{(a, a)} = {a^mba^m; m ≥ 0}, K = Q_{(λ, b)} = {b^m; m ≥ 0}. Zřejmě je M_{(a, a)} = M, M_{(Λ, b)} = N, K_{(Λ, b)} = K. Každý prvek množiny P je roven některému z derivativů L, Q, N, M, K, takže S = {L̅, Q̅, N̅, M̅, K̅} R₁ = {(L̅, aQ̅a), (L̅, N̅b), (Q̅, aM̅a), (Q̅, K̅b), (M̅, aM̅a), (M̅, N̅b), (K̅, K̅b)}, R₂ = {(Q̅, Λ), (N̅, Λ), (K̅, Λ)}, G(V, L, C) = (S, V, R₁ ∪ R₂, L̅). Je zřejmé, že G(V, L, C) generuje jazyk (V, L). □

 

7. Závěr. Z našich výkladů vyplynulo, že uvedené konstrukce morfologických a syntaktických kategorií lze zařadit do Willeho teorie pojmů, kterou pak lze dále podřídit teorii úplných svazů (srov. Birkhoff, 1948, kap. IV; Szász, 1963, s. 68—72). Náš článek je tedy ilustrací faktu, že touž matematickou teorii lze často aplikovat v různých oblastech reálného světa, takže oblasti, které spolu nijak nesouvisí, mohou mít podobný matematický popis. Užitečnost syntaktických kategorií z odst. 4 se ukazuje při konstrukci zobecněných gramatik, kde tyto kategorie hrají roli neterminálních symbolů.

 

LITERATURA

 

BIRKHOFF, G.: Lattice theory. New York 1948.

DOBRUŠIN, R. L.: Elementarnaja grammatičeskaja kategorija. Bjulleteň Objedinenija po problemam mašinnogo perevoda, 1957, No 5, s. 19—21.

DOBRUŠIN, R. L.: Matematičeskije metody v lingvistike. Matematičeskoje prosveščenije, 6, 1961, s. 37—60.

CHYTIL, M.: Automaty a gramatiky. Praha 1984.

KŘÍŽ, B.: Zobecněné gramatické kategorie. Kandidátská dis. práce. Univerzita J. E. Purkyně, Brno 1980.

KŘÍŽ, B.: Generalized grammatical categories in the sense of Kunze. Archivum Mathematicum Brno, 17, 1981, s. 151—158.

[120]KUNZE, J.: Versuch eines objektivierten Grammatikmodells I, II. Zeitschrift für Phonetik, Sprachwissenschaft und Kommunikationsforschung, 20, 1967, s. 415—448 a 21, 1968, s. 421—466.

MARCUS, S.: Sur un modèle logique de la catégorie grammatical élémentaire I. II, III. Revue des mathématiques pures et appliquées, 7, 1962, s. 91—107 a s. 683—691 a Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 8, 1962, s. 323—329.

MARCUS, S.: Analyse contextuelle. Zeitschrift für Phonetik, Sprachwissenschaft und Kommunikationsforschung, 18, 1965, s. 301—313.

NOVOTNÝ, M.: Abstract grammatical categories. PSML, 7, 1981, s. 151—165.

WILLE, R.: Restructuring lattice theory: an approach based on hierarchies of concepts. Technische Hochschule Darmstadt. Preprint-Nr. 628, Oktober 1981; také in: Ordered sets. Ed. I. Rival. Dordrecht - Boston 1982, s. 445—470.

SZÁSZ, G.: Introduction to lattice theory. Budapest 1963.

 

R É S U M É

Grammatical categories vs. concepts in situations

Wille’s method of concept forming is known from algebraic linguistics where Kunze and Kříž used it to introduce morphologic and syntactic categories, respectively. We investigate the relationship between Wille’s concepts and Kunze’s and Kříž’s categories.

By a situation we mean an ordered triple (G, M, r) where G, M are sets and r ⊆ G × M. Elements in G are interpreted to be objects, elements in M to be features, (g, m) ∈ r means that g has the feature m. For any X ⊆ G and any Y ⊆ M, we put

s(X) = {m ∈ M; (g, m) ∈ r for any g ∈ X},

t(Y) = {g ∈ G; (g, m) ∈ r for any m ∈ Y},

p(X) = t(s(X)).

Then the ordered pair (p(X), s(X)) is the concept generated by the set X in the sense of Wille, p(X) is its extent, and s(X) its intent.

Let (V, L) be a language, i.e., V is a finite set and L is a subset of the set V* of all stringe over V.

If taking V for G and V* × V* for M and if (a, (u, v)) ∈ r means nav ∈ L for any a ∈ V and any (u, v) ∈ V* × V*, then (V, V* × V*, r) is a situation and p(X) is a morphologic category in the sense of Kunze for any X ⊆ V.

If taking V* for G, V* × V* for M and if (x, (u, v)) ∈ r means uxv ∈ L for any x ∈ V* and any (u, v) ∈ V* × V*, then (V*, V*× V*, r) is a situation and p(X) is a syntactic category in the sense of Kříž for any X ⊆ V*.

Utility of Kříž’s syntactic categories is demonstrated by introducing generalized grammars where those categories play the role of nonterminals.

Slovo a slovesnost, ročník 49 (1988), číslo 2, s. 111-120

Předchozí Milada Hirschová: Uplatňování negace ve výpovědích s performativní platností

Následující Jana Hoffmannová a kol.: Mezioborová konference o interpretačních procesech