Nejasné jevy a jejich vyjasnění
Ladislav Nebeský
[Articles]
Non-transparent phenomena and their clarification
[1]1. Povšimněme si těchto dvou řádků s podivnými řetězy písmen, interpunkčních znamének a mezer:
V !ásledující v!t! jsou písme!! e, í ! p !!hr!ze!! ot!z!íkem.
V ?ř?dcház?j?c? větě jsou ??sm?na a, ě a n nahraz?na vykřičn?k?m.
Abychom mohli o každém z obou řetězů pohodlně hovořit, označíme je (ve shodě s jejich pořadím) jako (1) a (2). Řetězy (1) a (2) nám poslouží jako příklady nejasných jevů.
K nejasným jevům budeme řadit jak nezáměrná znejasnění v (psaném či mluveném) textu (např. zaviněná tiskovými chybami či šumem), tak i znejasnění zcela záměrná, kupř. vytečkování tabuizovaného slova nebo jeho nahrazení opisem; zkomolení údajů o osobě, jejíž totožnost nemá být prozrazena; jakékoli zamlžení textu sloužící jako hádanka nebo jako test.
Nejasné jevy nás vyzývají k rozluštění, tedy k nalezení toho, co se za nimi skrývá; tuto výzvu někdy ignorujeme, jindy se zájmem přijímáme. Přijmeme-li ji, rozluštění je někdy snadné (skrytost tu může být pouhou konvencí), ale jindy se nám třeba nemusí podařit. Připusťme i to, že rozluštění odhalí více rovnocenných řešení a že ani tehdy, když šlo o znejasnění záměrné, nemusel si být jeho autor všech možných řešení předem vědom.
Jestliže nejasný jev rozluštíme, potom to, co jsme odhalili, nazveme jeho vyjasněním. Pokud nejasný jev vznikl záměrně, jeho vyjasnění ho nemůže bez následků nahradit; doplnění tabuizovaného slova za jeho vytečkování, prozrazení osoby uvedením jejích přesných údajů, záměna testu s připojeným řešením za test k řešení teprve zadaný může mít nepříjemné důsledky. Avšak i tehdy, když nejasný jev vznikl nezáměrně, mohla být jeho existence podnětem k vzniku textu, který na něj reagoval; nahrazení nejasného jevu jeho vyjasněním před zánikem takového textu by vedlo k vzniku nového nejasného jevu (např. kdyby k druhému vydání nějaké knihy bylo přiloženo upozornění na chyby z prvního vydání, které však již jsou nyní opraveny).
Vraťme se k dvojici nejasných jevů (1) a (2). Jejich vyjasnění nalezneme snadno. Jsou to tyto věty, které označíme (1*) a (2*):
V následující větě jsou písmena e, í a p nahrazena otazníkem.
V předcházející větě jsou písmena a, ě a n nahrazena vykřičníkem.
Kdybychom na okamžik připustili, že věty (1*) a (2*) vypovídají jedna o druhé, shledali bychom, že vypovídají nepravdivě; jenomže ony jedna o druhé nevypovídají vůbec (proto jsme mezi ně vložili prázdný řádek). Vyjasnění (1*) jevu (1) pravdivě vypovídá o jevu (2): upozorňuje na to, jak se jev (2) od svého vyjasnění liší; a naopak, (2*) pravdivě vypovídá o (1): upozorňuje na to, jak se (1) liší od [2](1*). Jedno k druhému obě vyjasnění jen nepřímo poukazují; objevování věty (1*) pomáhá objevit větu (2*) a naopak.
Díky způsobu vzájemného provázání nejasných jevů a jejich vyjasnění nacházíme v dvojici (1) a (2) příklad v jistém směru mezní. Na podobné příklady lze nahlížet jako na pouhé jazykové hříčky; lze je však přijímat i jinak, uvědomíme-li si, že zájem o nejasné jevy je vlastní některým uměleckým proudům: dvojici nejasných jevů (1) a (2) by bylo možno považovat třeba za produkty tzv. experimentální poezie.[2]
Je však ještě jiný důvod, pro který by nás dvojice (1) a (2) mohla zajímat. Připomíná totiž vlekoucí se polemiku dvou autorů, kteří střídavě usvědčují jeden druhého z nepřesností. To, co je v jejich vzájemné polemice rozptýleno, v dvojici (1) a (2) nacházíme soustředěno.
Již těch několik málo příkladů, které jsme uvedli, naznačuje, že téma nejasných jevů je velice široké. Pokus o průzkum jeho šíře však cílem tohoto krátkého článku rozhodně není.[3] Naším záměrem je využít takových mezních příkladů, jako je dvojice (1) a (2), k pokusu o „jasnější“ vhled do spojení nejasných jevů s jejich vyjasněními.
2. Lze takové příklady, jako je dvojice (1) a (2), vytvářet i na základě jiného jazyka než přirozeného? Brzy ukážeme, že ano. Abychom to ukázali, budeme definovat velmi jednoduchý (i když dosti neobvyklý) umělý jazyk, který nazveme jazykem P. Jako jsme překročením přirozeného jazyka vytvořili dvojici nejasných jevů (1) a (2), tak překročením jazyka P vytvoříme jinou dvojici nejasných jevů.[4] Jakkoli bude jazyk P přirozenému jazyku omezeností svého užití i podobou svých „vět“ nesmírně vzdálen, patrně shledáme, že dvojice jevů, kterou překročením jazyka P vytvoříme, bude dvojici (1) a (2) blízká. To, že budeme s to na základě vhodného umělého jazyka vytvářet příklady blízké dvojici (1) a (2) vytvořené na základě jazyka přirozeného, napovídá, že tato dvojice jevů nevznikla shodou povrchních okolností, ale že se v ní setkáváme s příkladem něčeho obecnějšího.
Avšak abychom mohli nějakou dvojicí nejasných jevů jazyk P překročit, musíme ho nejprve definovat. Jak uvidíme, bude to jazyk, jenž pomocí jistých obrazců vypovídá o jiných obrazcích.
Uvažujme rovinu rozdělenou myšlenými řádky a sloupci na myšlená pole; takto rozdělenou rovinu si lze představit jako nekonečně velkou stránku čtverečkovaného papíru.[5] Kterákoli „věta“ (dále již bez uvozovek) jazyka P vypovídá o soustavě tvořené konečnou neprázdnou množinou prvků, z nich každý je umístěn v některém [3]poli (různé prvky v polích různých).[6] Abychom prvky jedné soustavy oddělili od prvků, které do ní nepatří, budeme ji ohraničovat pravoúhlým rámečkem; tento rámeček k soustavě poukazuje, není však její součástí.[7]
V souvislosti s jazykem P je důležité rozlišit soustavy čtvercové a zlomkovité. Řekneme, že soustava je čtvercová, když existuje celé kladné číslo n takové, že druhá mocnina tohoto čísla se rovná počtu prvků soustavy a kromě toho, když n > 1, tak prvky soustavy jsou rozmístěny na n po sobě následujících řádcích a na n po sobě následujících sloupcích; číslo n potom nazveme délkou strany této čtvercové soustavy.[8] Soustavám, které čtvercové nejsou, budeme říkat zlomkovité.
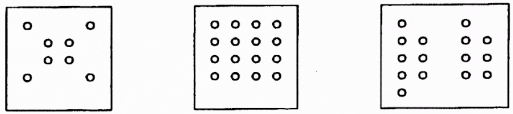
Na obr. 1 jsou představeny tři soustavy; ta prostřední je čtvercová soustava o straně délky 4, obě krajní soustavy jsou zlomkovité. Povšimněme si zlomkovité soustavy napravo. Má 15 prvků. Přidáním dalšího prvku by z ní vznikla soustava o 16 prvcích, ale ať bychom nový prvek přidali na jakékoli pole, vždy to bude soustava zlomkovitá. Pokud bychom ze soustavy napravo chtěli přidáním dalších prvků získat čtvercovou soustavu, museli bychom jich přidat 10 (tím by vznikla čtvercová soustava o straně délky 5) nebo 21 (tím by vznikla čtvercová soustava o straně délky 6) nebo 34 (tím by vznikla čtvercová soustava o straně délky 7) atd. Jak ihned uvidíme, naše pozorování má přímý vztah k větám jazyka P.
Obr. 1
Každá věta jazyka P vypovídá o nějaké zlomkovité soustavě. Přitom má každá věta jazyka P podobu čtvercové soustavy doplněné šipkou, která od ní míří k té zlomkovité soustavě, o níž věta vypovídá.[9] Předpokládejme, že o zlomkovité soustavě (řekněme) x vypovídá věta, která má podobu čtvercové soustavy o délce strany n (doplněná šipkou mířící k x); český překlad této věty jazyka P zní takto: k zlomkovité soustavě x lze přidat n nových prvků tak, aby z ní vznikla soustava čtvercová. Nepřehlédněme, že u zlomkovité soustavy, o níž věta vypovídá, je významný počet [4]jejích prvků, zatímco u čtvercové soustavy, pomocí níž věta vypovídá, je významná délky její strany.
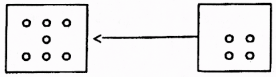
Obr. 2
Obr. 2 ukazuje zlomkovitou soustavu (řekněme) y o 7 prvcích spolu s větou, která o ní (čtvercovou soustavou o straně délky 2) vypovídá (v českém překladu) toto: k zlomkovité soustavě y lze přidat dva nové prvky tak, aby z ní vznikla soustava čtvercová.[10] Tato věta jazyka P je zřejmě pravdivá. Pokud bychom v této větě čtvercovou soustavu o délce strany 2 postupně nahrazovali čtvercovou soustavou o délce strany 9, 18, 29, 42, 57 …, získali bychom tím další pravdivé věty o zlomkovité soustavě y, k níž šipka věty míří.[11]
Věty jazyka P tedy vypovídají o zlomkovitých soustavách. Vypovídají o nich, jak z nich vzniknou soustavy čtvercové. A vypovídají o tom pomocí čtvercových soustav. Nyní, když již o větách jazyka P víme, jakou mají podobu a také o čem co a jak vypovídají, můžeme se začít vyjadřovat úsporněji. Místo o větách budeme někdy hovořit o čtvercových soustavách, které (spolu s šipkami) věty tvoří. Takto bychom např. řekli, že na obr. 2 čtvercová soustava napravo pravdivě vypovídá o zlomkovité soustavě nalevo.
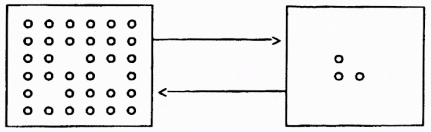
Teprve nyní, když je nám jazyk P znám, můžeme svůj zájem přenést na jevy, které věty tohoto jazyka připomínají, ale přitom jeho větami nejsou, neboť jejich definici překračují. Opřeni o znalost jazyka P zaměříme svoji pozornost na obr. 3. Vidíme na něm dvě zlomkovité soustavy, soustavu nalevo a soustavu napravo, a dvě šipky, které míří navzájem opačným směrem. Soustava nalevo (resp. napravo) spolu s šipkou, která od ní míří k soustavě napravo (resp. nalevo), je jevem, jenž označíme (3) (resp. (4)). Jev (3) připomíná větu jazyka P, která vypovídá o zlomkovité soustavě napravo, jev (4) připomíná větu, která vypovídá o zlomkovité soustavě nalevo. Ani jeden z jevů (3) a (4) větou jazyka P není, protože soustava, která ho (spolu s šipkou) tvoří, není čtvercová.
Jevy (3) a (4) jazyk P překračují, a proto můžeme zaujmout postoj, že není důvod se o ně zajímat. Také však můžeme takový postoj nezaujmout. Potom patrně shledáme, že se jevy (3) a (4) od vět jazyka P nevzdalují natolik, aby nestálo za to připustit, že jde o nejasné jevy, jejichž vyjasnění lze odkrýt. Přijmeme-li nejasné jevy (1) a (2) jako inspirační vzor, tak vyjasnění jevů (3) a (4) opravdu odkrýt lze, a to třeba jen jediným šťastným náhledem. Spolehlivěji však k jejich vyjasněním dojdeme úvahou, např. podobnou té, jež v petitu následuje.
[5]
Obr. 3
Podívejme se znovu na obr. 3.
Od soustavy nalevo míří šipka k soustavě napravo. Aby (v souladu s jazykem P) soustava nalevo pravdivě vypovídala o zlomkovité soustavě napravo, musela by být čtvercovou soustavou o straně délky 1, 6, 13, 22, … . Ve skutečnosti je však zlomkovitou soustavou o 33 prvcích. Míří k ní šipka od soustavy napravo. Aby (v souladu s jazykem P) soustava napravo pravdivě vypovídala o soustavě nalevo, musela by být čtvercovou soustavou o straně délky 3, 16, 31, … . Jenomže ona je zlomkovitou soustavou o 3 prvcích.
Předchozí odstavec bychom mohli opakovat znovu a znovu, můžeme však také pokračovat jinak. Nekonečnou posloupnost 1, 6, 13, 22, … a nekonečnou posloupnost 3, 16, 31, … jsme objevili nezávisle jednu na druhé. Z každé z nich však můžeme vybrat po jednom jejím členu, a ty již na sobě navzájem závisí: K soustavě nalevo
lze přidat 3 vhodné prvky tak, aby se z ní stala čtvercové soustava. Byla by to čtvercová soustava o straně délky 6. Ta by o soustavě vpravo pravdivě vypovídala, že k ní lze přidat 6 vhodných prvků, aby se z ní stala čtvercová soustava. Byla by to čtvercová soustava o straně délky 3. Ta by o soustavě vlevo pravdivě vypovídala, že k ní
Tím, jak začíná a končí, předcházející odstavec překračuje hranice psané podoby přirozeného jazyka. Mohli bychom ho číst znovu a znovu (nedokončenou poslední větu lze dokončit první větou, které chybí začátek). Avšak kvůli tomu, co jsme chtěli odkrýt, si stačí předchozí odstavec přečíst jen jednou. Kromě o dvou zlomkovitých soustavách, které vidíme na obr. 3, hovoří se v něm o dvou soustavách čtvercových. Každá z nich zastupuje jednu z obou zlomkovitých soustav v tom smyslu, že za ni vypovídá o té druhé zlomkovité soustavě. Čtvercové soustavy (spolu se šipkami ukazujícími k zlomkovitým soustavám, o nichž vypovídají) jsou vyjasněními jevů (3) a (4).
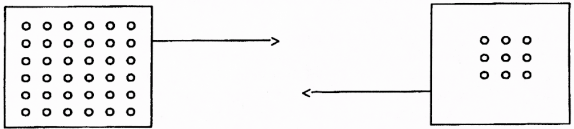
Obr. 4
Vyjasnění jevů (3) a (4), k nimž nás dovedla úvaha tištěná petitem, označíme (3*) a (4*). Najdeme je na obr. 4; (3*) je vlevo, (4*) vpravo. Vyjasnění (3*) o čtvercovém útvaru ve vyjasnění (4*) vypovídat nemůže a vyjasnění (4*) o čtvercovém útvaru ve vyjasnění (3*) také ne. Jedno k druhému obě vyjasnění jen nepřímo poukazují; objevujeme-li (3*), objevujeme i (4*) a naopak. Vzájemným provázáním jevů (3) a (4) s jejich vyjasněními je tato dvojice nejasných jevů srovnatelná s dvojici (1) [6]a (2), což jsme chtěli ukázat. Podobně provázaných dvojic nejasných jevů, jako je dvojice jevů (3) a (4), lze překročením jazyka P vytvářet nekonečně mnoho.[12]
3. Vytváření nejasných jevů na základě přirozeného jazyka může spoléhat na složité sítě konotací, které jsou s užíváním přirozeného jazyka svázány, tedy na něco, co u umělého jazyka, jaký jsme zde definovali, postrádáme. Proto nám při vytváření nejasných jevů na základě jazyka P byla vzorem vzájemně provázaná dvojice jevů (1) a (2).[13] Soustředili jsme se tedy na takové nejasné jevy, v nichž – metaforicky řečeno – jazyk pozoruje sám sebe.
Dvojice jevů (1) a (2) vzdáleně připomíná logické antinomie, tedy jazykové jevy, které již od starověku provokují lidské myšlení. Příbuzenský vztah mezi nejasnými jevy, které nás zde zajímají, a logickými antinomiemi bude zřejmější, když si místo dvojice (1) a (2) povšimneme jen jediného nejasného jevu, který je však vystavěn obdobně, např. tohoto jevu, jež označíme jako (5):[14]
* této *ětě je malé i *elké písmeno * nahrazeno h*ězdičkou.
Vidíme však, že mezi logickými antinomiemi na jedné straně a nejasnými jevy, jako je (5), na straně druhé jde jen o příbuzenství vzdálené. Logické antinomie vedou – stručně řečeno – ke kruhovému pohybu mezi výrokem a jeho negací. Snadno rozluštitelná věta – označíme ji (5*) – která je vyjasněním jevu (5), nevypovídá o sobě, ale o tomto jevu; napětí mezi (5) a (5*) můžeme vnímat jako trvalé,[15] avšak rozdílnost úloh obou členů této dvojice způsobuje, že k takovému kruhovému pohybu jako u logických antinomií zde nedochází.[16]
Závěrem: V druhém oddílu tohoto článku jsme si všímali umělého jazyka, který jsme definovali s nezvyklým záměrem: ne abychom se v jeho hranicích pohybovali, ale abychom je o kousek překročili. Na takto nezvyklý záměr lze jistě nepřistoupit. [7]To, že jsme na něj přistoupili, nám umožnilo vytvářet „umělé“ nejasné jevy a nalézat jejich „umělá“ vyjasnění. A to nám zase rozšířilo pohled na nejasné jevy (2), (3), (5) a jejich vyjasnění (2*), (3*) a (5*) jako na příklady něčeho obecnějšího, co je užívání jazyka o jazyku potenciálně vlastní.
LITERATURA
LYONS, J.: Semantics. Volume 1. Cambridge University Press Cambridge, 1977.
QUINE, W. V.: Word and Object. M.I.T. Press, Cambridge, Mass. 1960.
Vrh kostek (česká experimentální poezie). Ed. J. Hiršal a B. Grögerová. TORST, Praha 1993.
R É S U M É
Non-transparent phenomena and their clarification
The subject matter of the paper are non-transparent phenomena in language usage. The attention is given to a pair of non-transparent phenomena created on the basis of written Czech language (by crossing its boundary): each member of this pair reflects the non-transparency of the other. A simple formal artificial language (of geometric nature), called language P, is defined here. A pair of non-transparent phenomena comparable to the pair mentioned above is created on the basis of language P (by crossing its boundary). The solution (clarification) of such pairs of non-transparent phenomena is considered.
[1] Tento článek vznikl s podporou grantu č. 405/95/1554 GA ČR. – Autor upřímně děkuje Pavlu Novákovi za cenné připomínky k předběžné podobě rukopisu. Bohumilovi Palkovi autor vděčí za podnět k pozn. 3.
[2] Autor tohoto článku v 60. letech opravdu podobné artefakty v rámci experimentální poezie vytvářel. Kupř. jeho „text“ z r. 1965 třináctihlasí (sborník Vrh kostek, s. 88) tvoří 13 různě provázaných nejasných jevů; vyjasnění každého z nich upozorňuje na počet písmen, o nějž má některý z ostatních jevů méně než jeho vyjasnění.
[3] Zaznamenejme však alespoň, že do širokého tématu nejasných jevů by bylo možno zařadit i to, co W. V. Quine (1960, s. 141n.) nazval referenční nejasností (referential opacity). Srov. Lyons, 1977, s. 192–193.
[4] Jestliže zde (a později znovu) hovoříme místo o češtině obecněji o přirozeném jazyku, je to proto, že dvojici nejasných jevů (1) a (2) lze přetlumočit do jiného jazyka, sice jenom velmi volně, ale při zachování toho, co je pro tuto dvojici jevů charakteristické.
[5] Tento článek je psán pro čtenáře – nematematiky. Autor chápe, že případný čtenář – matematik bude některé formulace vnímat jako nejasné jevy; věří však, že takový čtenář jejich vyjasnění snadno odhalí.
[6] Některé čtenáře (zejména poté, co se seznámí s podobou vět jazyka P) patrně napadne, že by bylo vhodné definici soustavy doplnit tak, aby připouštěla, že soustava může nějak změnit polohu, aniž by tím ztratila totožnost. Pro tyto čtenáře doplňme definici takto: pokud bychom soustavu posunuli o nějaký počet sloupců doleva nebo doprava a o nějaký počet řádků nahoru nebo dolů tak, že by se přitom nezměnila vzájemná poloha jejích prvků, výslednou soustavu budeme považovat za totožnou se soustavou výchozí.
[7] Protože rámeček není částí soustavy, můžeme ho zvětšovat, zmenšovat i posunovat, pokud přitom každý prvek soustavy zůstává uvnitř rámečku a pokud každý prvek, který do soustavy nepatří, zůstává vně. S ohledem na další výklad stojí za to dodat, že kdyby soustava měla být rozšířena přidáním dalších prvků, není toto rozšiřování rámečkem omezeno: rámeček lze vhodně zvětšit vždy.
[8] Soustava o jediném prvku je čtvercovou soustavou o straně délky 1.
[9] Je třeba, aby se rámečky obou soustav nedotýkaly, nekřížily, ani neležel jeden uvnitř druhého. Jinak na vzájemné poloze obou útvarů nezáleží.
[10] Dodejme, že to bude čtvercová soustava o straně délky 3.
[11] Budou pravdivé, protože k zlomkovité soustavě o 7 prvcích představené na obr. 2 můžeme přidat 9 (resp. 18, 29, 42, 57) prvků tak, aby tím vznikla čtvercová soustava o straně délky 4 (resp. 5, 6, 7, 8).
[12] Uvažujme libovolnou dvojici celých kladných čísel j a k takových, že j ≤ k, že čísla j2 – k a k2 – j jsou kladná a že ani jedno z čísel j2 – k a k2 – j není druhou mocninou celého čísla. Soustava, která má j2 – k vhodně rozmístěných prvků spolu se soustavou, která má k2 – j vhodně rozmístěných prvků, jež jsou doplněny dvojicí šipek směřujících od každé z obou soustav k té druhé, je dvojicí nejasných jevů jako (3) a (4). Povšimněme si, že na obr. 3 je j = 3 a k = 6. To, že takových dvojic jevů jako na obr. 3 lze vytvářet nekonečně mnoho, je dáno již tím, že pro libovolné celé kladné číslo j větší než 1 lze za číslo k zvolit číslo j; každá z obou soustav bude potom mít j2 – j vhodně rozmístěných prvků (způsobem jejich rozmístění se však tyto dvě soustavy mohou různit).
[13] Zatímco luštěním dvojice jevů (3) a (4) jsme se zabývali podrobně, tím, jak nacházíme věty (1*) a (2*), které jsou vyjasněním jevů (1) a (2), jsme se nezabývali – uhádnout věty (1*) a (2*) bylo snadné. Lze si však představit dvojici jevů mnohem nejasnějších, u níž by se jakýkoli postup vedoucí k dvojici vět, která jevy vyjasňuje, členil do řady netriviálních kroků. (Bylo by zajímavé zkoumat, při jakém „množství nejasnosti“ pokus o vyjasnění již ztroskotá.)
[14] I nejasné jevy podobné jevu (5) lze vytvářet překročením jazyka P. Každý takový jev by měl podobu zlomkovité soustavy doplněné šipkou, která z ní vychází a také v ní končí; jak lze vyčíst z pozn. 11, tato zlomkovitá soustava by měla 2 prvky nebo 6, 12, 20, 30, … prvků rozmístěných tak, aby přidáním dalších 2 nebo 3, 4, 5, 6, … prvků mohla vzniknout čtvercová soustava o straně délky 2 nebo 3, 4, 5, 6, … . Vyjasněním tohoto jevu by potom byla čtvercová soustava (o straně některé z délek 2 nebo 3, 4, 5, 6, …); ta by nevypovídala o sobě, ale zato by pravdivě vypovídala o zlomkovité soustavě nejasného jevu.
[15] Právě tato možnost vnímat napětí mezi nejasnými jevy a jejich vyjasněními v dvojici (1) a (2) jako trvalé nás vedla k jejich připodobnění k některým artefaktům experimentální poezie.
[16] Věta (5*) vypovídá o jevu (5), jehož je vyjasněním, pravdivě. K tomu, abychom získali nejasný jev, jehož vyjasněním je věta, která o něm vypovídá nepravdivě, stačí jev (5) obměnit takto:
* této *ětě není ani malé ani *elké písmeno * nahrazeno hvězdičkou.
Slovo a slovesnost, volume 58 (1997), number 1, pp. 1-7
Previous Objednací lístek
Next Eva Koktová: Ke klasifikaci českého souvětí
© 2011 – HTML 4.01 – CSS 2.1