Morfologické značkování korpusu českých textů stochastickou metodou

Jan Hajič, Barbora Hladká

[Články]

(pdf)

Morphological tagging of Czech using stochastic methods

1. Úvod

Až do nedávné doby sloužil jako podklad k lingvistickému výzkumu ručně excerpovaný materiál z tištěných nebo mluvených textů. Podobně byly vytvářeny i slovníky. Pro účely moderních počítačových aplikací byly do počítače vkládány slovníky vytvořené speciálně pro tu kterou aplikaci, většinou opět na základě výběru z existujících tištěných slovníků, a jednotlivé lexikální jednotky byly opatřeny morfologickými a gramatickými údaji dodávanými ručně. V posledním desetiletí se velmi rychle rozvíjí tzv. korpusová lingvistika (Čermák, 1995). V mnoha zemích se pro jednotlivé jazyky vytvářejí počítačové korpusy textů a vyvíjejí se programy pro opatřování jednotlivých slovních výskytů v textech morfologickými, popř. i některými syntaktickými údaji, jako je slovní druh, informace o morfologických kategoriích daného slovního tvaru (např. rod, číslo, pád u podstatných jmen, osoba, číslo, čas, způsob a vid u sloves) atd. Tyto údaje nazýváme značky (tagy) a proces přiřazování značek slovům označujeme jako značkování (tagování). Pro ilustraci uvádíme příklad značkování slov značkami, které byly navrženy v experimentu pravděpodobnostního značkování českých textů (jejich seznam viz odd. 3.1):

 

Redakce|NFS1	(podstatné jméno-N, rod ženský-F, číslo jednotné-S, pád první-1)
Slova|NNS2	(podstatné jméno-N, rod střední-N, číslo jednotné-S, pád druhý-2)
a|SS	(spojka-S, souřadící-S)
slovesnosti|NFS2	(podstatné jméno-N, rod ženský-F, číslo jednotné-S, pád druhý-2)
vyzývá|V3SAPOFA	(sloveso-V, osoba třetí-3, číslo jednotné-S, slovesný rod činný-A, čas přítomný-P, způsob oznamovací-O, rod ženský-F, pozitivní sloveso-A)
své|PSMP4	(přivlastňovací zájmeno svůj-PS, rod mužský životný-M, číslo množné-P, pád čtvrtý-4)
přispěvovatele|NMP4	(podstatné jméno-N, rod mužský, životný-M, číslo množné-P, pád čtvrtý-4)

 

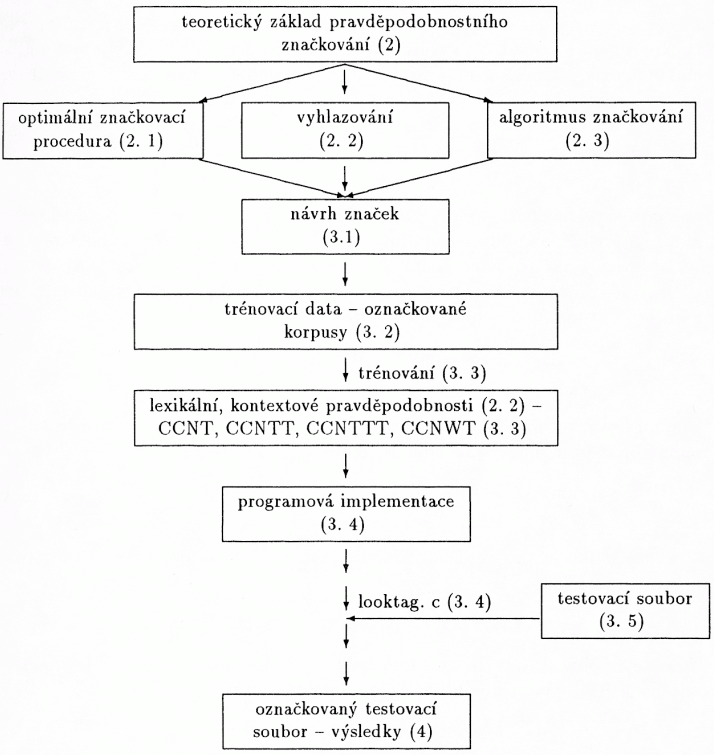
Ruční značkování je ovšem velmi zdlouhavé a navíc nepřesné a nekonzistentní: jeden korpus značkuje více lidí, jejich názory na přiřazení jednotlivých údajů se mohou různit, ovšem ani jeden člověk nezaručí konzistenci. Jsou proto vyvíjeny procedury, které by umožňovaly automatické nebo poloautomatické (ručně tak či onak kontrolované) přiřazování značek. V poslední době se zkoušejí postupy, které realizují automatické přiřazování značek na základě pravděpodobnostních metod. Pravděpodobnostní formulace problému značkování vychází z následujících předpokladů: existuje kvalitní teoretický základ, pravděpodobnosti poskytují přímou cestu k zjednoznačnění[1] značky pro dané slovo a pravděpodobnosti mohou být odhadnu[289]ty automaticky přímo z dat. Jednotlivé kroky pravděpodobnostního morfologického značkování jsou zachyceny v následujícím obrázku. U každého hesla je uvedeno číslo odstavce, ve kterém je podán detailnější popis.

 

 

2. Teoretický základ pravděpodobnostního značkování

Nechť je definována množina značek, potom značkování je procedura Φ, která textu W = w₁w₂ … w_n přiřadí posloupnost značek T = t₁t₂ … t_n, kde w₁, w₂, …, w_n jsou jednotlivá slova textu W a t₁, t₂, …, t_n jsou značky z definované množiny značek (slovu w_i je přiřazena značka t_i). Symbolicky toto přiřazení můžeme zapsat Φ(W, T); mluvíme pak o jediné posloupnosti značek T, T = Φ(W).

 

[290]2. 1. Optimální značkovací procedura

Pravděpodobnostní postupy vycházejí právě z toho, že jednotlivá přiřazení Φ(W, T) (viz výše) jsou generována podle pravděpodobnostního rozdělení p(W, T). Hledají se podmínky pro optimální značkovací proceduru, která zajistí nejlepší výsledky vzhledem ke zvolenému algoritmu a také vzhledem k datům, se kterými pracuje. Náš experiment (viz odd. 3.) vychází z práce Merialdovy (1992), kde je velice přirozeně stanovena podmínka pro optimální pravděpodobnostní značkovací proceduru takto:

 

Φ(W) =	argmax	p(T|W)	(1)
	T

 

tzn. hledá se taková posloupnost značek T, která při daném vstupním textu W maximalizuje příslušnou podmíněnou pravděpodobnost (p je pravěpodobnostní rozdělení). Použitím Bayesova teorému o podmíněných pravděpodobnostech (Jaglom – Jaglom, 1964) na rovnost (1) vznikne další matematická rovnost vyjadřující podmínku pro optimální značkovací proceduru:

 

Φ(W) =	argmax	p(W|T) × p(T)/p(W)	(2)
	T

 

Jinými slovy, vstupní text W známe, p(W) je sice neznámé, ale pevné číslo, které se nemění, ať jsou značky jakékoli. Můžeme tedy (2) přepsat na:

 

Φ(W) =	argmax	p(W|T) × p(T)	(3)
	T

 

Pravděpodobnost posloupnosti značek T = t₁t₂ … t_n se pomocí Bayesova teorému vypočítá následovně: 

 

p(T) = p(t1, t2, …, tn) = p(t1) × p(t2|t1) × … × p(tn|t1, t2, …, tn–1)

(4)

 

Pravděpodobnost věty W za podmínky, že posloupnost značek T je známa, se po aplikaci Bayesova teorému vyjádří matematicky takto:

 

p(W|T) = p(w1, w2, …, wn|t1, t2, …, tn) =
= p(w1|t1, t2, …, tn–1) × … × p(wn|t1, w1, t2, …, wn–1, tn–1, tn)	(5)

 

Nabízí se otázka, jak zvolit příslušné pravděpodobnostní rozdělení p. Odpověď zní: z trénovacích dat. Jako trénovací data slouží pro pravděpodobnostní značkování správně (vzhledem k možnostem) označkované (např. ručně) korpusy (= soubory textů, kde ke každému slovu je přiřazena právě jedna značka).

Značka pro daný slovní výskyt se určuje na základě tvaru slova i kontextu. V případě bigramové verze značkování se uvažuje značka předcházejícího slova a v případě trigramové verze značkování se uvažují značky dvou předcházejících slov. Je možné si zvolit libovolně dlouhý kontext, ale experimenty ukazují, že nejvhodnější je volit právě kontext o délce dvou nebo tří slov.

Na základě této úvahy provedeme následující aproximace. Pravděpodobnost slova w závisí pouze na jeho značce t, v bigramovém modelu pravděpodobnost značky [291]závisí pouze na předcházející značce a v trigramovém modelu pravděpodobnost značky závisí pouze na dvou předchozích značkách. Na základě těchto aproximací můžeme zapsat definitivní tvar podmínky pro optimální značkovací proceduru pro bigramovou i trigramovou verzi:

 

• bigramová verze 

			n
Φ(W) =	argmax	p(w1|t1) ×	∏	p(wi|ti) × p(ti|ti–1)	(6)
	T		i=2

  

• trigramová verze 

				n
Φ(W) =		argmax	p(w1|t1) × p(w2|t2) × p(t2|t1) ×	∏	p(wi|ti) ×
		T		i=2
	× p(ti|ti–1, ti–2)					(7)

kde n je počet slov vstupního textu W, w_i jsou jednotlivá slova textu W, t_i jsou značky z definované množiny značek přiřazované slovům w_i, i je pořadí slova v textu.

Z označkovaných korpusů se snadno získají frekvence f(w, t) (kolikrát je slovo w označkováno značkou t), f(j, i) (kolikrát je značka j následována značkou i) nebo f(j, i, k) (kolikrát se vyskytuje posloupnost značek j, i, k za sebou). Na základě těchto frekvencí se vypočítají relativní frekvence příslušných jevů a prostřednictvím nich se odhadnou (tzv. natrénují) lexikální p(w|t) a kontextové p(t_i|t_i–1), p(t_i|t_i–2, t_i–1) pravděpodobnosti. Lexikální pravděpodobnost je pravděpodobnost označkování slova w značkou t (p(w|t) = f(w, t)/f(t)). Kontextová pravděpodobnost bigramová je pravděpodobnost výskytu značky j následované značkou i (p(i|j) = f(j, i)/f(j)) a kontextová pravděpodobnost trigramová je pravděpodobnost výskytu značky j následované značkou i následovanou značkou k (p(k|j, i) = f(j, i, k)/f(j, i)). Pro ilustraci uvažujme nyní v trénovacím korpusu označkovanou část věty:

 

Redakce|NFS1 Slova|NNS2 a|SS slovesnosti|NFS2 vyzývá|V3SAPOFA přispěvatele|NMP4

 

Lexikální pravděpodobnost p(slovesnosti| NFS2) = f(slovesnosti, NFS2) / f(NFS2), tedy pravděpodobnost, že značkou NFS2 pro podstatné jméno (N) rodu ženského (F), čísla jednotného (S), pádu druhého (2) bylo označkováno slovo „slovesnosti“, je dána podílem počtu výskytů (frekvencí – f(slovesnosti, NFS2)) dvojice „slovesnosti, NFS2“ v trénovacím korpusu a celkovým počtem výskytů (frekvencí – f(NFS2)) značky NFS2. Pokud tedy bylo slovo „slovesnosti“ desetkrát označkováno značkou NFS2 a značka NFS2 se vyskytla šedesátkrát v trénovacím korpusu, potom lexikální pravděpodobnost je 0,6. Kontextová pravděpodobnost

– bigramová: p(NFS2| SS) = f(SS, NFS2) / f(SS), tedy pravděpodobnost, že značce NFS2 předchází značka SS, je dána podílem počtu výskytů (frekvencí – f(SS, NFS2)) dvojice značek „SS, NFS2“ v trénovacím korpusu a celkovým počtem [292]výskytů (frekvencí – f(SS)) značky SS. Pokud se v trénovacím korpusu vyskytla dvojice po sobě následujících značek SS, NFS2 třikrát a značka SS se vyskytla dvanáctkrát, potom kontextová pravděpodobnost značek NFS2 a SS je 0,4.

– trigramová: p(V3SAMOFA| SS, NFS2) = f(SS, NFS2, V3SAMOFA) / f(SS, NFS2), tedy pravděpodobnost, že značce V3SAMOFA předcházejí značky SS a NFS2, je dána podílem počtu výskytů (frekvencí – f(SS, NFS2, V3SAMOFA)) trojice značek „SS, NFS2, V3SAMOFA“ v trénovacím korpusu a celkovým počtem výskytů (frekvencí – f(SS, NFS2)) dvojice po sobě následujících značek SS, NFS2. Pokud se v trénovacím korpusu vyskytla trojice po sobě následujících značek SS, NFS2, V3SAMOFA dvakrát a dvojice SS, NFS2 se vyskytla dvacetkrát, potom kontextová pravděpodobnost značek V3SAMOFA, NFS2 a SS je 0,1.

 

2. 2. Vyhlazování (smoothing)

V případě jevů, které se v trénovacím textu nevyskytly (dvojice slov, značka, dvojice značek, trojice značek), se pravděpodobnost rovná nule. V testovacím souboru se však tyto jevy vyskytnout mohou. Nulová pravděpodobnost je problém, který může nepříznivě ovlivnit další průběh značkovací procedury. K vyřešení problému se používá tzv. vyhlazování, při kterém dochází k interpolaci pravděpodobnostního rozdělení p takto:

 

λw1 ∊ (0, 1), λt1, λt2, λt3 ∊ (0, 1)	(8)
p(w|t) = λw1 × p(w|t) + (1 – λw1) × p0(w)	(9)
p'(ti|ti–1) = λt1 × p(ti|ti–1) + λt2 × p(ti) + (1 – λt1 – λt2) × p0(ti)	(10)
p'(ti|ti–1, ti–2) = λt1 × p(ti|ti–1, ti–2) + λt2 × p(ti|ti–1)+
+ λt3 × p(ti) + (1 – λt1 – λt2 – λt3) × p0(ti)	(11)

 

kde

 

p0(w) = 1/|W|, |W| je počet slovních tvarů trénovacího souboru,	(12)
p0(ti) = 1/|T|, |T| je počet všech různých značek trénovacího souboru.	(13)

 

Kromě intuitivního odhadu koeficientů λ_w1, λ_t1, λ_t2, λ_t3, o který se v našem experimentu opíráme, je jednou z možných metod zjištění vyhlazovacích koeficientů interpolační algoritmus, tzv. EM-algoritmus; vzhledem k malému množství trénovacích dat jsme však tuto metodu nepoužili. Pomocí vztahů (8)–(13) zapíšeme upravené rovnice pro optimální značkovací proceduru. 

• bigramová verze 

			n
Φ(W) =	argmax	p'(w1|t1) ×	∏	p'(wi|ti) × p'(ti|ti–1),	(14)
	T		i=2

[293]• trigramová verze 

				n
Φ(W) =		argmax	p'(w1|t1) × p'(w2|t2) × p'(t2|t1) ×	∏	p'(wi|ti) ×
		T		i=3
	× p'(ti|ti–1, ti–2)					(15)

 

2. 3. Algoritmus značkování

Na závěr popisu teoretického základu značkování charakterizujeme vlastní algoritmus značkování, tzv. Viterbiho algoritmus. Hlavní myšlenkou tohoto algoritmu je sestrojování vícevrstevného hranově ohodnoceného grafu, ve kterém hledáme cestu maximální délky splňující naše kritéria optimální značkovací procedury (viz (14), (15)). Celkový počet vrstev grafu odpovídá počtu slov značkovaného textu a i-tá vrstva odpovídá zpracování i-tého slova značkovaného textu. Nechť T_i je množina možných značek pro i-té slovo textu, n_i je velikost množiny T_i, potom i-tá vrstva grafu obsahuje právě n_i uzlů označených značkami z příslušné množiny T_i. Každé dva vrcholy ze sousedních dvou vrstev jsou spojeny hranou. Ohodnocení těchto hran vychází právě z podmínky pro optimální značkovací proceduru. Pokud vstupní text obsahuje k slov, potom v takto sestrojovaném grafu existuje n₁ × n₂ × … × n_k různých cest, které pokrývají vrcholy všech vrstev. Pro delší texty W je však tento algoritmus „hrubé síly“ prakticky nepoužitelný. Jeho tzv. varianta trellis využívá toho, že aproximované rozdělení p'(t_i|t_i–1) závisí na předešlé značce (pro bigramovou verzi značkování). V i-tém kroku algoritmu proto již můžeme pro možnou dvojici t_i–1, t_i vybrat mezi všemi cestami t₁, …, t_i končícími touto dvojicí tu, která má největší hodnotu p'(w₁, …, w_i|t₁, …, t_i) a všechny ostatní „zapomenout“, neboť bez ohledu na volbu značek na místech i + 1, i + 2, … se hodnota p'(w₁, …, w_i|t₁, …, t_i) již nemění vzhledem k tomu, že násobení kladných čísel zachovává monotonii. Uvažujme část věty Redakce Slova a slovesnosti vyzývá, kterou chceme označkovat, a bigramovou verzi značkování. Budeme postupně konstruovat graf, který obsahuje pět vrstev (vstupní věta obsahuje pět slov). Při konstrukci vycházíme z konkrétních čísel odvozených z „upraveného“ korpusu (viz odd. 3. 2.). V tomto korpusu bylo slovo redakce označkováno 7 × jako NFS1, 8 × jako NFS2, slova 44 × jako NNP1, 27 × jako NNP4, 78 × jako NNS2, a 1 × jako F, 322 × jako K, 19 360 × jako SS. Slova slovesnosti a vyzývá se v korpusu nevyskytla. Celkový počet slovních tvarů v korpusu je 72 445, celkový počet slov je 621 015, celkový počet různých značek je 1 171 a příslušné vyhlazovací koeficienty (viz odd. 2. 2.) nabývají hodnot: λ_w1 = 0.999, λ_t1 = 0,99, λ_t2 = 0,009.

Dále jsme z korpusu získali následující údaje relevantní pro uvedenou značkovanou strukturu: f(NFS1) = 11 759, f(NFS2) = 16 347, f(NNP1) = 816, f(NNP4) = 741, f(NNS2) = 8 180, f(F) = 196, f(K) = 2 039, f(SS) = 32 231, f(NFS5) = 0, f(NFP1) = 0, f(NFP4) = 0, f(NFP5) = 0, f(NFS1, NNS2) = 273, f(NFS1, NNP1) = 1, f(NFS1, NNP4) = 1, f(NFS1, NNP5) = 0, f(NNS2, SS) = 837, f(NNS2, K) = 15, f(NNS2, F) = 0.

 

[294]PRVNÍ VRSTVA[2]: 

Redakce	p’(redakce|t), kde t ∊ {NFS1, NFS2, NFS5, NFP1, NFP4, NFP5} (viz pozn. č. 1)
NFS1	0,999 × 7/11 759	+1/72 445 = 6 × 10–4
NFS2	0,999 × 8/16 347	+1/72 445 = 5 × 10–4
NFS5	0	+1/72 445 = 1,38 × 10–5
NFP1	0	+1/72 445 = 1,38 × 10–5
NFP4	0	+1/72 445 = 1,38 × 10–5
NFP5	0	+1/72 445 = 1,38 × 10–5

 

PRVNÍ a DRUHÁ VRSTVA[3]:

Redakce	p’(redakce|NFS1) × p(slova|t2) × p(t2|NFS1), kde t2 ∊ {NNS2,		slova
	NNP1, NNP4, NFP5} (viz pozn. č. 1)
NFS1	(6 × 10–4) × (0,999 × 78/8 180 + 1,38 × 10–5) ×		NNS2
	(0,99 × 273/11 759 + 0,009 × 8 180/621 015 +
	0,001 × 1/1 171)	= 0,13 × 10–6
	(6 × 10–4) × (0,999 × 44/816 + 1,38 × 10–5) ×		NNP1
	(0,99 × 1/11 759 + 0,009 × 816/621 015 + 0,001 ×
	1/1 171)	= 0,0031 × 10–6
	(6 × 10–4) × (0,999 × 37/741 + 1,38 × 10–5) ×		NNP4
	(0,99 × 1/11 759 + 0,009 × 741/621 015 + 0,001 ×
	1/1 171)	= 0,0029 × 10–6
	(6 × 10–4) × (0 + 1,38 × 10–5) × (0 + 0 + 0,001 ×		NNP5
	1/1 171)	= 0,006624 × 10–12
Redakce	p(redakce|NFS2) × p(slova|t2) × p(t2|NFS2), kde t2 ∊ {NNS2,		slova
	NNP1, NNP4, NFP5} (viz pozn. č. 1)
NFS2	(5 × 10–4) × (0,999 × 78/8 180 + 1,38 × 10–5) ×		NNS2
	(0,99 × 345/16347 + 0,009 × 8180/621 015 +
	0,001 × 1/1171)	= 0,1 × 10–6
	(5 × 10–4) × (0,999 × 44/816 + 1,38 × 10–5) ×		NNP1
	(0,99 × 2/16347 + 0,009 × 816/621015 + 0,001 ×
	1/1 171)	= 0,0036 × 10–6
	(5 × 10–4) × (0,999 × 37/741 + 1,38 × 10–5) ×		NNP4
	(0,99 × 2/16 347 + 0,009 × 741/621 015 +
	0,001 × 1/1171)	= 0,0033 × 10–6
	(5 × 10–4) × (0 + 1,38 × 10–5) × (0 + 0 + 0,001 ×		NNP5
	1/1 171)	= 0,00552 × 10–12

 

Porovnáme-li ohodnocení všech hran mezi první a druhou vrstvou, zjistíme, že hrana určená vrcholy NFS1, NNS2 je ohodnocena největší hodnotou. Vzhledem k úvahám provedeným na začátku tohoto odstavce, můžeme všechny ostatní hrany zapomenout a dále pracovat pouze s jednou vybranou hranou (NFS1, NNS2).

 

DRUHÁ a TŘETÍ VRSTVA 

slova	p(redakce|NFS1) × p(slova|NNS2) × p(a|t3) × p(t3|NNS2), kde t3 ∊ {SS,		a
	F, K} (viz pozn. č. 1)
NNS2	(0,13 × 10–6) × (0,999 × 19 360/32 231 + 1,38 × 10–5) ×		SS
	(0,99 × 837/8 180 + 0,009 × 32 231/621 015 + 0,001 ×
	1/1 171)	= 0,008 × 10–6
	(0,13 × 10–6) × (0,999 × 1/196 + 1,38 × 10–5) × (0 +		F
	0,009 × 196/621 015 + 0,001 × 1/1 171)	= 0,002 × 10–12
	(0,13 × 10–6) × (0,999 × 322/2 039 + 1,38 × 10–5) ×		K
	(0,99 × 15/8 180 + 0,009 × 2 039/621 015 + 0,001 ×
	1/1 171)	= 0,0001 × 10–6

 

Z výpočtů ohodnocení je vidět, že pracujeme s malými čísly. Proto po zpracování hran vedoucích z jednoho konkrétního uzlu se provede normalizace příslušných ohodnocení hran. Nechť z libovolného uzlu vede k hran, e_i je ohodnocení i-té hrany, [295]potom nové ohodnocení i-té hrany e'_i se určí následovně:

 

	k
e'i = (1/	∑	ej) × ei
	j=1

 

Po druhé a třetí vrstvě zkonstruujeme analogickým postupem čtvrtou a pátou vrstvu. Ze všech hran mezi čtvrtou a pátou hranou vybereme hranu s nejvyšším ohodnocením. Tato hrana je jednoznačně určena dvěma vrcholy – vrcholy ze čtvrté a páté vrstvy. Ohodnocení těchto uzlů přiřadíme po řadě čtvrtému a pátému slovu. Příslušná vybraná hrana je poslední hranou jednoznačně určené cesty, která vede z vrcholu páté vrstvy do vrcholu první vrstvy. Procházíme-li cestu od poslední (v našem případě páté vrstvy) vrstvy do první vrstvy, přiřazujeme ohodnocení vrcholů (značky) cesty slovům značkovaného textu. Pokud bychom dopočítali ohodnocení všech hran grafu pro naši vstupní větu, dostali bychom v grafu hledanou cestu a tím označkování slov vstupní věty:

 

Redakce		Slova		a		slovesnosti				vyzývá
NFS1		NNS2		F			NFS2			V3SAPOMA
NFS2		NNP1		K			NFS3			V3SAPOIA
NFS5		NNP4		SS			NFS6			V3SAPONA
NFP1		NNP5					NFP1			V3SAPOFA
NFP4							NFP4
NFP5							NFP5

 

V experimentu pravděpodobnostního značkování českých textů jsme provedli malou modifikaci značkovacího algoritmu. Pro každé slovo uvažujeme jako množinu možných značek všechny značky, které se vyskytly v trénovacím souboru, a ne výstup morfologické analýzy slova. To znamená, že každá vrstva grafu obsahuje stejný počet vrcholů a tento počet je roven počtu značek v trénovacím souboru. Zapojení morfologické analýzy je další cesta, kterou se budeme dále ubírat (viz odd. 4).

 

3. Experiment pravděpodobnostního značkování českých textů

Jak již bylo v úvodu řečeno, jsou vyvíjeny procedury, které by umožňovaly automatické přiřazování značek. Jedním z postupů, které se v této oblasti uplatňují, je postup založený na pravděpodobnostních metodách. Z dosavadních publikací o pravděpodobnostním značkování je zřejmé, že nebyl dosud proveden experiment pravděpodobnostního značkování pro slovanský jazyk. Dále z publikovaných údajů (např. Brill, 1993; Church, 1992) vyplývají vysoká procenta úspěšnosti pravděpodobnostního značkování anglických textů. Při těchto výsledcích se okamžitě objeví otázka, s jakými výsledky by proběhl experiment provedený pro jakýkoli slovanský jazyk, tím spíše pro náš, český jazyk. Proto jsme začali experimentovat nad pravděpodobnostním značkováním českých textů. Cílem našeho experimentu bylo tedy zjistit, zda lze pravděpodobnostních metod použít i pro jazyk flexívního typu s bohatstvím koncovek, které vedou ke značnému množství značek přiřazovaných slovům. Výsledky, kterých jsme dosáhli, jsou diskutovány v odst. 4. V této části naší stati budeme charakterizovat dílčí kroky, které směřují k automatickému pravděpodobnostnímu značkování.

 

[296]3. 1. Návrh značek

Značky je třeba navrhovat pro každý jazyk individuálně. V našem experimentu jsme vycházeli ze základního dělení slov do deseti slovních druhů a pro každý slovní druh značky popisují jeho základní morfologické kategorie. V tabulce 1 uvádíme v přehledu uplatňované morfologické kategorie, jejich označení a hodnoty, kterých mohou nabývat, v tabulce 2 přiřazujeme tyto kategorie jednotlivým slovním druhům. Obě tabulky v souhrnu pak podávají přehled o množině značek, které jsme v experimentu používali.

  

Morfologická kategorie	Označení (viz tab. 2)	Možné hodnoty	Popis
rod	g	M	mužský životný
		I	mužský neživotný
		N	střední
		F	ženský
číslo	n	S	jednotné
		P	množné
čas	t	M	minulý
		P	přítomný
		F	budoucí
způsob	m	O	oznamovací
		R	rozkazovací
pád	c	1	nominativ
		2	genitiv
		3	dativ
		4	akusativ
		5	vokativ
		6	lokativ
		7	instrumentál
rod	s	A	činný
		P	trpný
negace	a	N	negativní
		A	pozitivní
stupeň	d	1	positiv
		2	komparativ
		3	superlativ
osoba	p	1	první
		2	druhá
		3	třetí

Tab. 1

 

[297]Slovní druh
podstatná jména	Ngnc
	zkratky	NZ
přídavná jména	Agncda
slovesa
	infinitivy	VTa
	přechodníky	VWntsga
	ostatní tvary	Vpnstmga
zájmena
	osobní	PPpnc
	3. osoba	PP3gnc
	přivlastňovací	PRgncpgn
	svůj	PSgnc
	se	PEc
	ostatní	PDgnca
příslovce	Oda
spojky	Ssouřadící (S) / podřadící (P)
číslovky	Cgnc
předložky	Rpředložka
částice	F
citoslovce	K
konec věty	T_SB
interpunkce	T_IP
neznámá značka	X

Tab. 2

 

3. 2. Příprava trénovacích dat

Jak již bylo řečeno, pravděpodobnostní značkování je založeno na tréninku s označkovanými korpusy. Jako trénovací korpus jsme použili ručně označkovaný korpus, který vznikl během šedesátých a sedmdesátých let v odd. matematické lingvistiky Ústavu pro jazyk český Československé akademie věd, které nám také tento korpus poskytlo (Těšitelová, 1985). Tento korpus je rozdělen do 180 souborů jednotného formátu: jednotlivá slova spolu se svými značkami a s dalšími informacemi jsou na samostatném řádku. Značky použité v tomto korpusu se lišily od námi navržených značek (původní počet určovaných morfologických kategorií byl daleko vyšší, pro jednotlivé morfologické kategorie byly použity odlišné symboly), proto naším prvním úkolem bylo provést odpovídající konverze. Konverzemi jsme neměnili rozdělení korpusu do souborů ani formát souborů. Následující příklad ilustruje několik provedených konverzí.

  

slovo	značka ÚJČ[4]	nová značka
zesilovače	110221	NIP1
patří	5261 1	V3PAPOIA
do	772	Rdo
[298]takzvaných	25 222	AIP21A
aktivních	22 222	AIP21A
obvodů	117222	NIP2

 

Po provedení těchto konverzí jsme měli k dispozici korpus (dále „upravený“ korpus) s následujícími vlastnostmi.

 

počet slov	621 015
počet slovních tvarů	72 445
počet různých značek	1 171
průměrný počet značek na jedno slovo	3,65

Tab. 3

 

Malou část korpusu, která nebyla samozřejmě zahrnuta do trénování, jsme použili jako testovací soubor.

 

3. 3. Trénování

Vstupem pro trénování byl tedy „upravený“ korpus. Výstupem trénování jsou tři (v případě trigramové verze čtyři) soubory: V příkladech uvádíme první tři řádky souborů.

(i) soubor obsahující abecedně utříděné různé značky, které se vyskytly v korpusu; každé značce předchází její frekvence v korpusu;

 

Př.	2546	AFP11A
	81	AFP11N
	84	AFP21A

 

(ii) soubor obsahující abecedně utříděné různé dvojice (slovo, značka) z korpusu; každé dvojici předchází její frekvence v korpusu;

 

Př.	2	abc|NZ
	1	abecední|AIS11A
	1	abecedy|NFS2

 

(iii) soubor obsahující abecedně utříděné různé dvojice po sobě následujících značek z korpusu; každé dvojici předchází její frekvence v korpusu;

 

Př.	266	AFP11A|AFP11A
	9	AFP11A|AFP11N
	4	AFP11A|AFP12A

 

(iv) pro trigramovou verzi soubor abecedně utříděných různých trojic po sobě následujících značek; každé trojici předchází její frekvence v korpusu;

 

Př.	22	AFP11A|AFP11A|AFP11A
	1	AFP11A|AFP11A|AFP11N
	1	AFP11A|AFP11A|AFP13A

 

Z podstaty pravděpodobnostního značkování vyplývá požadavek na co největší soubor trénovacích dat. V rámci experimentu českého značkování jsme provedli dva dílčí pokusy, které se právě liší velikostí trénovacích dat (srov. tab. 3 a 4) a které jednoznačně charakterizují přímou závislost úspěšnosti experimentu na velikosti [299]trénovacích dat (viz tab. 5). Oba trénovací korpusy byly vyděleny z „upraveného korpusu“.

 

počet slov	110 874
počet slovních tvarů	22 530
počet různých značek	882
průměrný počet značek na jedno slovo	2,36

Tab. 4

 

3.4. Programové vybavení pro automatické značkování textů

Implementace automatického značkování textů byla provedena pod operačním systémem MS-DOS. Pro konverze (viz odd. 3.2.) byl použit softwarový produkt FLEX, který je vhodným prostředkem pro zpracování textových souborů. Pro ilustraci uvádíme část zdrojového kódu flexového programu, který provádí konverzi značek ÚJČ pro podstatná jména do námi navržených značek pro podstatná jména.

 

%%
[ ̂ |\n]*“|“	{ ECHO; BEGIN(INFO); }
<INFO>1	{BEGIN(START1); }
<INFO>[2-9]	{ ECHO; BEGIN(IGNORE); }
<START1>7	{ fprintf(yyout, “%s“, “NZ“); BEGIN(IGNORE); }
<START1>4	{ fprintf(yyout, “%s“, “C“); BEGIN(KONEC1); }
<START1>.	{ fprintf(yyout, “%s“, “N“); BEGIN(KONEC1); }
<KONEC1>[0-7|“ “]	{ BEGIN(ROD); }
<ROD>[1|2|3|4|9“ “]	{ fprintf (yyout, “%s“, rody[yytext[0]]); BEGIN(CISLO); }
<CISLO>[1|2|3|4|9|“ “]	{ fprintf (yyout, “%s“, cislo[yytext[0]]); BEGIN(PAD); }
<PAD>“ “	{ fprintf (yyout, “%“, “X“); BEGIN(IGNORE); }
<PAD>[1-7]	{ ECHO; BEGIN(IGNORE1); }
<IGNORE1>“ “	{ BEGIN(IGNORE);}
<IGNORE>.*\n	{ ECHO; BEGIN(INITIAL); }
%%

 

Pro vytvoření čtyř souborů[5] popsaných v odd. 3. 3. byly použity flexové programy a dávkové soubory op. systému DOS. Tyto soubory se staly podkladem pro vznik struktury slovníkového typu (dtag1.cpd). Program looktag.c, který realizuje značkovací algoritmus (vytvoření grafu, nalezení cesty), byl napsán v jazyce C. Tento program pracuje nad strukturou dtag1.cpd, ve které vyhledává frekvence pro výpočet lexikálních a kontextových pravděpodobností jevů. Značkovací program jako takový je samozřejmě jazykově nezávislý (např. viz odd. 4).[6]

 

[300]3. 5. Testování

Testovací soubor (tab. 5) – vstupní soubor programu looktag – byl oddělen jako část „upraveného“ korpusu, která ovšem nebyla zahrnuta do trénování. Testovací soubor obsahuje každé slovo na samostatném řádku. Výstupní soubor reprezentuje posloupnost značek, kterou značkovací program nalezl pro příslušný vstupní soubor.

 

4. Vyhodnocení výsledků

Pro zjištění procentuální úspěšnosti značkovacího programu bylo nutné porovnat značky ručně přiřazené se značkami přiřazenými programem. Pro ilustraci uvádíme na příkladu jedné věty srovnání ručního značkování s výsledky počítačového značkování; za každým slovem je uvedena nejprve ručně přiřazená značka a za další svislou čarou nejprve výsledek trigramového experimentu a nakonec výsledek bigramového experimentu (v obou experimentech byl jako trénovací soubor použit kompletní „upravený“ korpus). Kurzívou jsou vyznačeny případy, kdy se značky přiřazené programem lišily od ručně přiřazených značek.

 

slovo|ručně přiřazená značka| výsledek trigramového experimentu výsledek bigramového exp.
oficiálně|O1A| O1A O1A		naší|PRFS21QP| PRFS21QP PRFS21QP
uvítala|V3SAMOFA| V3SAMOFA		vlasti|NFS2| NFS2 NFS2
	V3SAMOFA	předsedkyně|NFS1| NFS1 NFS1
hrdinnou|AFS41A| AFS11A AFS11A		rady|NFS2| NFS2 NFS2
představitelku|NFS4| NFS1 NFS1		žen|NFP2| NFP2 NFP2
pokrokové|AFS21A| AFS21A AFS21A		Gusta|NFS1| T_SB T_SB
Ameriky|NFS2| NFS2 NFS2		Fučíková|NFS1| NFS1 NFS1
na|Rna| Rna Rna		a|SS| SS SS
půdě|NFS6| NFS6 NFS6		předseda|NMS1| NMS1 NMS1
úv|NZ| NZ NZ		Juraj|NMS1| NMS1 NMS1
ssm|NZ| NZ NZ		Varholík|NMS1| NMS1 NMS1

 

V tab. 5 uvádíme výsledky dvou bigramových experimentů, které se právě liší velikostí trénovacích dat. Výsledky ukazují, že čím větší trénovací soubor máme k dispozici, tím dosáhneme lepších výsledků. Dále tab. 5 charakterizuje výsledky bigramového a trigramového experimentu podle procenta úspěšnosti, tj. podle počtu správně přiřazených značek. V obou experimentech jsme použili stejný testovací soubor. Tyto výsledky naznačují, že obě verze mají v podstatě stejné procento úspěšnosti. V případě trigramového experimentu bychom k získání vyššího procenta úspěšnosti potřebovali podstatně větší trénovací soubor.

Pro zajímavost jsme provedli unigramový experiment, ve kterém pro dané slovo nebereme v úvahu žádný kontext, pouze jsme každému slovu přiřadili jeho nejpravděpodobnější značku z trénovacího souboru, který byl stejný jako v případě bigramového a trigramového experimentu. Neznámým slovům, která se nevyskytla v trénovacím korpusu, jsme přiřadili „pracovní“ značku (pro tento účel zvolenou) „XX“. K testování jsme použili stejný soubor jako pro bigramový a trigramový experiment.

 

[301]	Unigramový	Bigramový	Bigramový	Trigramový
	experiment	experiment	experiment	experiment
		(menší trénovací	(větší trénovací
		data – tab. 4)	data – tab. 3)
testovací data	1 294	1 294	1 294	1 294
(počet slov)
počet chybně	444	334	239	244
přiřazených značek
procento	65,70 %	74,19 %	81,53 %	81,14 %
úspěšnosti

Tab. 5 („upravený“ korpus)

 

Výsledky experimentů ukazují, že jakmile zapojíme do značkování kontext, procento úspěšnosti se zvýší o šestnáct procent. Následující tabulky podávají podrobnější rozbor chyb trigramového experimentu.

 

	A	N	C	P	R	S	T	X	O	V	F	K
A	32	6	0	2	2	2	1	0	3	2	0	0	50
N	4	64	0	0	4	2	5	4	8	2	0	0	93
C	0	1	4	0	0	0	0	0	0	0	0	0	5
P	0	0	0	19	0	0	1	2	3	0	0	0	23
R	0	1	0	0	0	0	0	2	1	0	0	0	4
S	0	0	0	0	0	0	0	2	0	0	0	0	2
T	0	1	0	0	0	0	0	0	0	0	0	0	1
X	0	0	0	5	0	1	0	0	0	2	0	0	8
O	0	1	0	0	0	0	1	0	0	1	0	0	3
V	0	3	0	0	3	8	1	2	8	28	0	0	53
F	0	0	0	0	0	0	0	0	0	0	0	0	0
K	0	0	0	0	0	1	0	1	0	0	0	0	2

Tab. 6

 

První sloupec a první řádek tab. 6 obsahují písmena označující jednotlivé slovní druhy, konec věty, interpunkci a neznámou značku. Celkový počet chybně přiřazených značek v trigramovém experimentu byl 244. Z tohoto celkového počtu bylo 50 chybně označkovaných přídavných jmen, 93 podstatných jmen, 5 číslovek, atd. (viz poslední sloupec tabulky). Čísla uvnitř tabulky udávají počet, kolikrát byly slovní tvary příslušného slovního druhu (odpovídající písmeno na řádku v prvním sloupci) chybně označkovány (viz název sloupce). Například dvakrát bylo přídavné jméno označkováno jako sloveso, dvakrát jako předložka, šestkrát jako podstatné jméno; v počtu 32 bylo přídavné jméno sice označkováno jako přídavné jméno, ale chyba nastala v dalším přiřazování morfologických kategorií. Statistiku těchto chyb poskytují následující tabulky.

 

A	g	n	c	g&c	g&n	c&a	g&n&c	g&c&d
32	17	1	6	3	2	1	1	1

Tab. 7.1

 

V sedmnácti případech mělo přídavné jméno chybně přiřazen rod, v jednom případě číslo, v šesti případech pád, ve třech případech rod i pád zároveň, atd.

 

[302]N	g	n	c	g&c	n&c	→ NZ
64	11	5	41	2	4	1

Tab. 7.2

 

Čísla v ostatních tabulkách jsou zřejmá, snad jen pro upřesnění: v jednom případě bylo podstatné jméno označkováno jako zkratka, v jednom případě ostatní zájmeno jako osobní, ve čtyřech případech obecné sloveso jako infinitiv.

 

C	g	c
4	1	3

Tab. 7.3

 

P	g	c	g&c	PD → PP
19	8	7	4	1

Tab. 7.4

 

V	p	t	n	s	n&t	p&t	t&a	g&a	p&n&t	V → VT
28	3	6	5	5	1	1	1	1	1	4

Tab. 7.5

 

Z celkového počtu 1 294 slov testovacího souboru bylo 105 neznámých slov; slov, která se nevyskytla v trénovacím souboru. Z celkového počtu neznámých slov bylo 6 slov správně označkováno, to tedy znamená, že úspěšnost značkovacího programu pro neznámá slova je 5,7 %.

 

Jak vysoké nebo jak nízké jsou uvedené úspěšnosti?

Posouzení, zda úspěšnost našeho experimentu je vysoká nebo nízká, vyplývá z porovnání úspěšností automatického značkování textů jiných jazyků. Vycházíme-li z experimentů pro slovanské a pro neslovanské jazyky, naše odpovědi zní takto:

Výsledky, kterých jsme dosáhli v našem experimentu, jsou lepší než jsme původně očekávali, a zároveň jsou prvními slavistickými výsledky experimentů tohoto druhu. Pro ostatní slovanské jazyky se dají očekávat přibližně stejně vysoká procenta úspěšnosti. Zároveň se dá také očekávat, že experimenty pro ostatní slovanské jazyky se budou potýkat se stejnými problémy, s jakými jsme se potýkali i my. Problémy míníme vysoký počet značek a malou velikost trénovacích dat.

V rámci porovnání výsledků s experimenty pro neslovanské jazyky jsme provedli vlastní experiment, ve kterém jsme použili náš značkovací program (looktag.c) a jako trénovací a testovací data posloužil Wall Street Journal - WSJ (Marcus – Santorini – Marcinkiewicz, 1992; Santorini, 1990). Tab. 7. 6 prezentuje výsledky experimentů, které jsou srovnatelné s výsledky uváděnými v literatuře. Pro všechny experimenty jsme použili stejný testovací soubor. V testovacím souboru se vyskytlo osmnáct neznámých slov, která byla v trigramovém experimentu označkována s přesností 67 %.

 

[303]	Unigramový	Bigramový	Trigramový
	experiment	experiment	experiment
testovací data (slova)	1 294	1 294	1 294
počet chybně přiřazených značek	136	41	37
procento úspěšnosti	89,49 %	96,83 %	97,14 %

Tab. 7.6 (WSJ)

 

Budeme-li porovnávat výsledky českého a anglického experimentu pouze jako samostatná čísla, vychází nám procentuální úspěšnost českého experimentu nízká. Takto však výsledky chápat nelze. Při porovnání výsledků pro slovanský a pro neslovanský jazyk musíme brát v úvahu především různé typologické vlastnosti jazyků. Rozdílnost mezi češtinou jako flexívním jazykem morfologicky nejednoznačným a angličtinou jako jazykem s chudou flexí se promítá např. ve velikosti množin značek – 45 pro anglický jazyk, 1 171 pro český jazyk, v počtu různých bigramů a trigramů (viz tab. 7. 7, 7. 8).

  

	Český		WSJ
	„upravený“
	korpus
x < = 4	24 064	x < = 10	459
4 < x <= 16	5 577	10 < x < = 100	411
16 < x <= 64	2 706	100 < x < = 1000	358
x > 64	1 581	x > 1000	225
Celkový počet bigramů	33 928	Celkový počet bigramů	1 453

Tab. 7. 7 – Počet bigramů s frekvencí x

 

	Český		WSJ
	„upravený“
	korpus
x <= 4	155 399	x < = 10	11 810
4 < x <= 16	16 371	10 < x < = 100	4 571
16 < x <= 64	4 380	100 < x < = 1000	1 645
x > 64	933	x > 1000	231
Celkový počet trigramů	177 083	Celkový počet trigramů	18 257

Tab. 7. 8 – Počet trigramů s frekvencí x

 

Závěrem můžeme tedy konstatovat, že se nám podařilo prokázat, že pravděpodobnostní metody lze použít i pro jazyk flexívního typu; pro získání větší úspěšnosti bude však třeba čistý statistický přístup něčím obohatit. Dalším krokem pak bude zapojení morfologické analýzy češtiny do značkovacího programu (Hajič, 1994), což povede ke zkomplikování procedury, ale také ke zvýšení její úspěšnosti. V tomto směru zaměřujeme nyní svůj další výzkum.

Projekt českého tagování a příprava jazykových dat je součástí grantu GAČR 405/96/K214 a projektu MŠMT VS96151.

 

LITERATURA

 

BRILL, E.: A Corpus Based Approach To Language Learning. PhD Dissertation in Department of Computer and Information, Science, University of Pennsylvania 1993.

[304]ČERMÁK, F.: Jazykový korpus: Prostředek a zdroj poznání. SaS, 56, 1995, s. 119–140.

HAJIČ, J.: Unification Morphology Grammar. Doktorská dizertace. MFF UK, Praha 1994.

CHURCH, K. W.: Current practice in part of speech tagging and suggestions for the future. In: H. Kučera, Studies in Slavic Philology and Computational Linguistics. Michigan Slavic Publications, Ann Arbor 1992.

JAGLOM, A. M. – JAGLOM, I. M.: Pravděpodobnost a informace. Nakladatelství Československé akademie věd, Praha 1964.

MARCUS, M. P. – SANTORINI, B. – MARCINKIEWICZ, M. A.: Building a large annotated corpus of English: The Penn Treebank. Computational Linguistics, 1993, s. 313–330.

MERIALDO, B.: Tagging text with a probabilistic model. Computational Linguistics, 1992, s. 155–171.

SANTORINI, B.: Part of Speech Tagging Guidelines for the Penn Treebank Project. Technical report MS-CIS-90-47, Department of Computer and Information Science, University of Pennsylvania 1990.

TĚŠITELOVÁ, M. a kol.: Kvantitativní charakteristiky současné češtiny. Academia, Praha 1985.

 

R É S U M É

Morphological tagging of Czech using stochastic methods

Tagging inflectional languages has recently becom a „hot“ topic in computational linguistics. In contrast to English, where it is common to obtain almost 97% accuracy using a relatively small tagset (around 70 tags, mostly expressing syntactic properties of a given word form), Czech and other inflectional languages pose a much harder problem. The Czech tagset contains well over 1000 different tags, which combine all common morphological categories. The average number of tags per token in a text is around 3.5 and every other token can be tagged by two or more tags. We have developed one possible method for automatic disambiguation of morphological tags. This method has been compared to other methods and similar results have been obtained. Also, we show the influence of the tagset size to overall accuracy of the disambiguation process. Error analysis of the results is presented in detail.

Slovo a slovesnost, ročník 58 (1997), číslo 4, s. 288-304

Předchozí Miroslav Červenka, Květa Sgallová: Verš a věta. Rytmické a větné členění v české poezii druhé poloviny 19. století

Následující Jan Kořenský: Mezi mluvnicí a naukou o jazyku