Vztah formy a funkce v jazyce (Pokus o axiomatizaci)

Ladislav Nebeský, Petr Sgall

[Articles]

(pdf)

Отношение формы и функции в языке (Попытка аксиоматизации) / Le rapport entre la forme et la fonction dans la langue (Un essai d’axiomatisation)

1. V současné jazykovědě se rychle rozvíjí zkoumání vztahů uvnitř jazykového systému formálními (matematickými, logickými) metodami, zejména v souvislosti s prací na nových úkolech, jako je příprava strojového překladu a jiného automatického zpracování údajů z textu. Formální metody se uplatňují zejména v popisu vztahů syntaktických,[1] ale objevují se už i práce věnované formálnímu studiu vztahu mezi jazykovou formou (prostředkem, výrazem) a funkcí (obsahem, významem).[2]

Existuje několik základních koncepcí tohoto vztahu. Pražská škola funkčně strukturální vypracovala chápání vztahu formy a funkce jako vztahu několikastupňového; tento vztah je tu viděn mezi hláskou a fonémem, mezi zvukovou podobou a funkcí morfému, mezi jednotkami morfologickými (pády aj.) a syntaktickými (větnými členy aj.), popř. i mezi některými dalšími jednotkami.[3] Naproti tomu glosematika spatřuje vlastní vztah mezi výrazem a obsahem jen v rovině morfému, kdežto ostatní výše uvedené vztahy řadí jinam.[4]

[175]Celá otázka se nově klade v souvislosti s uvedenými úkoly aplikované lingvistiky, které vyžadují důsledné rozlišení postupu „od funkce k formě“ a „od formy k funkci“ a co nejúspornější relativně úplný popis jazykového systému v obou těchto aspektech. Při sestavování algoritmů pro strojový překlad je třeba řešit na různých úrovních jazykového systému jednak homonymii (a polysémii), tj. zjistit obecná kritéria rozlišující, v kterém případě má daná forma jednu a v kterém druhou ze svých možných funkcí (při analýze textu ve vstupním jazyce), a jednak synonymii, tj. zjistit měřítka pro výběr jedné ze dvou nebo více forem téže funkce (při syntéze textu ve výstupním jazyce). Své důsledky má toto rozlišení ovšem i pro jiná uplatnění jazykovědy, kde se s ním více nebo méně soustavně pracuje, jako např. v metodice jazykového vyučování.[5]

Pro teorii i aplikace jazykovědy jsou tedy aktuální dvě základní otázky týkající se vztahu formy a funkce: I. Jde ve fonologii, syntaxi ap. o týž vztah jako v morfologii ap., nebo nikoli? Lépe řečeno: v čem se tyto vztahy shodují a v čem se rozcházejí? II. Je oprávněn předpoklad, podle něhož různé roviny jazykového systému se z hlediska vztahu formy a funkce nepřekrývají (platí tedy vztah funkce a formy bezprostředně jen mezi jednotkami dvou sousedních rovin)?

K tomu se pak druží otázky další, zejména: III. Podle jakých měřítek lze jazykové jednotky třídit do různých rovin vztahu formy a funkce (a kolik rovin je třeba rozlišovat)? IV. Jaké jsou specifické vlastnosti každé roviny, či jak je možno roviny třídit? V. Týká se rozdělení jazykových jednotek do rovin přímo vztahu formy a funkce, nebo se jednotky seskupují do rovin podle své struktury a vztah formy a funkce je relativní (podobně jako vztah části a celku, příčiny a následku ap.), tedy sám o sobě různé roviny jednotek nevytváří?

Úkolem článku není na tyto otázky odpovědět, nýbrž jen připravit určité předpoklady k tomu, aby se odpovědi mohly hledat asi takovým postupem: Aby se pokud možno jednoznačně ukázalo, které rysy jsou vztahu funkce a formy v různých rovinách společné a které jsou specifické a aby bylo možno podle prostudovaných vztahů morfologických a fonologických[6] zjistit, do jaké míry jsou tytéž rysy charakteristické i pro vztahy ve vyšších, zatím ne dost soustavně prozkoumaných rovinách (lexikální sémantika, významová výstavba věty, kontextové členění výpovědi), k tomu je nejvhodnější pokusit se vytvořit axiomatický systém,[7] který by mohl sloužit jako popis vztahu formy a funkce na kterémkoli stupni. Vycházíme přitom z poměrně slabých předpokladů: počítáme předběžně sice s tím, že roviny jsou úplné a nepřekrývají se, ale také s tím, že postavení jednotek v řetězcích vztahu formy a funkce určuje rozdělení jednotek jen ve velmi malé míře (srov. odst. 5). Další zkoumání ukáže, jak bude třeba tyto výchozí předpoklady upravit.

2. Tento článek má být dílčím příspěvkem ke zpřesnění pracovních postupů v lingvistice. Lingvistické pojmy a vztahy mezi nimi bývají často definovány nebo vymezovány pomocí pojmů příliš málo jasných, nezačleněných do systému, popř. logickým kruhem. Vhodnější postupy jsou umožněny prostředky moderní logiky [176]a matematiky;[8] k nim patří i axiomatizace, která mj. zajišťuje, že se při definování operuje (vedle pojmů definovaných) jen poměrně malým počtem základních (výchozích) pojmů, které uvnitř soustavy výslovně definovány nejsou, ale jsou charakterizovány právě soustavou axiómů. Chtěli bychom zdůraznit, že obsahem článku není žádná rozvinutá axiomatická teorie, nýbrž jen soubor axiómů a definic směřující k jasnějšímu učlenění vztahů mezi některými základními pojmy z oblasti vztahu formy a funkce v jazyce. Náš soubor axiómů je přirozeně volen tak, aby se pojmy na jeho základě definované co nejvíce shodovaly s pojmy lingvistické teorie budované empiricky, v níž pojmy vznikají často spíše jen vedle sebe, bez jasného učlenění vzájemných vztahů.

Někdy se tvrdí, že lingvistické pojmy jsou příliš složité, než aby se daly s úspěchem formalizovat. Domníváme se, že složitost pojmu je v podstatě dvojího typu: a) hranice pojmů nejsou zcela přesné (jsou vágní), b) vztah pojmu vzhledem k ostatním (nebo alespoň k těm, jež považujeme za základnější) nelze danými prostředky stručně zachytit. Tento druhý typ složitosti může být právě výhodně popsán prostředky formalizace; definice a výroky pak mohou být podstatně stručnější, a dovedeme-li jich užívat, orientujeme se v jejich logické struktuře daleko snadněji než u týchž výroků formulovaných beze zbytku v přirozeném jazyce. A na druhé straně míru vágnosti pojmů lze nejlépe postihnout, snažíme-li se je definovat prostřednictvím pojmů již dříve definovaných. Tím se jejich hranice zpřesní, popř. se jeden pojem rozčlení na několik nových ap.

Budeme axiómy, definice a tvrzení zapisovat pomocí formálního aparátu, kterého užívá A. Grzegorczyk.[9] Užíváme symbolů teorie množin a predikátového kalkulu; symboly nám slouží především jako zkratky prostředků přirozeného jazyka. Vedle symbolicky zapsaných definic (D) uvádíme pro většinu pojmů také ne zcela systematická vysvětlení nebo přepis definice do přirozeného jazyka.[10] Písmena A, B … označují množiny; A ∪ B označuje množinu skládající se z těch prvků, které leží aspoň v jedné z označených množin (sjednocení); A ∩ B označuje množinu těch prvků, které leží současně v množině A i B (průnik); jako A ⊂ B zapíšeme, že množina A je podmnožinou (částí) množiny B (přičemž se připouštějí oba extrémní případy: B ⊂ B, ∅ ⊂ B, kde ∅ označuje prázdnou množinu). Jako x ∊ A zapíšeme výrok „x je prvkem množiny A“; symbol {x₁, …, x_n} označuje množinu složenou z vyznačených prvků. U výroků, zapsaných zde obecně jako p, q, budeme symbolem p ∧ q značit jejich konjunkci (p a zároveň q), symbolem p ∨ q disjunkci (p nebo q), symbolem p → q implikaci (jestliže p, pak q), symbolem p ≡ q ekvivalenci (p tehdy a jen tehdy, když q) a symbolem ~ p negaci (non p). Symboly ⋀ a ⋁ označují obecný (velký) a existenční (malý) kvantifikátor: výrok ⋀ x ∊ A (P (x)) čteme „pro každé x z množiny A platí P (x); výrok ⋁ x ∊ A (P (x)) čteme „existuje takové x v množině A, že platí P (x).

3. Uvedeme základní pojmy, s kterými budeme v našem článku pracovat. V prvé řadě to bude neprázdná konečná množina forem Φ a neprázdná konečná množina funkcí Φ'. Dále budeme vycházet z množiny individuálních kontextů forem [177]a funkcí Γ. Nebudeme však přímo pracovat s individuálními kontexty, nýbrž s jejich neprázdnými množinami; tyto množiny individuálních kontextů nazveme teprve kontexty. K výchozímu pojmu našeho systému dále patří jednoargumentová funkce C a dvě trojargumentové funkce K a K'.[11] C přiřazuje každému prvku x z množiny Φ ∪ Φ' (tj. každé formě nebo funkci) nějaký kontext (tj. neprázdnou podmnožinu množiny Γ), který označíme C (x); v našem systému to bude množina všech individuálních kontextů, v nichž se x vůbec vyskytuje. K přiřazuje všem trojicím x, A, B — kde x je forma, A a B neprázdné množiny funkcí — nějaký kontext nebo prázdnou množinu (tj. nějakou podmnožinu množiny Γ); označíme je K (x, A, B). K' přiřazuje všem trojicím x, A, B — kde x je funkce, A a B neprázdné množiny forem — nějaký kontext nebo prázdnou množinu (tj. nějakou podmnožinu množiny Γ); označíme je K' (x, A, B). Pokud K (x, A, B) je neprázdná množina, pak je to v našem systému ten kontext, v němž forma x z množiny svých funkcí A vyjadřuje funkce B, tj. relevantní rys kontextu vymezující tento vztah.[12] Ve zvláštním případě, kdy B = {y} (tj. kdy množina B má jen jeden prvek), budeme psát prostě K (x, A, y);[13] jde tu o relevantní rys kontextu, který odlišuje jednu funkci formy x od jejích funkcí jiných (těch, které jsou ostatními prvky množiny A). Podobně K' (x, A, y) označuje ten kontext, v němž je funkce x ze svých forem A vyjadřována právě formou y. Posledním výchozím pojmem je pevně daná neprázdná množina kontextů, kterou označíme Δ; budeme jí rozumět systém „nižších“ kontextů (srov. pozn. k axiómu 6).

Vidíme, že výchozí pojmy jsou dosti složité. Domníváme se však, že systém vycházející z pojmů jednodušších by znamenal deformaci některých rysů metody, s kterou lingvistika k otázkám vztahu formy a funkce přistupuje; např. o kontextech se v lingvistice mluví často právě jako o kritériích (při synonymii a homonymii), takže je třeba pracovat s jejich relevantními rysy, popř. s množinami kontextů, které jsou těmito rysy vymezeny, srov. naše K (x, A, B); v jiném smyslu se o kontextu mluví, konstatuje-li se např., že se určitá jednotka vyskytuje právě v takových a takových kontextech, čemuž odpovídá naše množina C (x).

Uvedeme nyní soupis axiómů.[14] V jejich zápisu pro přehlednost vynecháváme obecné kvantifikátory (pokud se v témž axiómu neobjevují i kvantifikátory existenční), čímž se zápis podstatně zkrátí, aniž dojde k nedorozumění; další zjednodušení, s kterým tu pracujeme: je-li A množina a označíme-li A* systém jejích podmnožin, pak budeme místo ⋀ B ∊ A* (popř. ⋁ B ∊ A*) psát ⋀ B ⊂ A (popř. ⋁ B ⊂ A).

A1: (K (x, A, B) ≠ ∅) → (K (x, A, B) ∩ C (x) ≠ ∅)

A1': (K' (x, A, B) ≠ ∅) → (K' (x, A, B) ∩ C (x) ≠ ∅)

 

[178]A2: ((B₁ ⊂ A₁) ∧ (B₂ ⊂ A₂)) → ((K (x, A₁, B₁) ≠ ∅) ∧ K (x, A₂, B₂) ≠ ∅) ≡
≡ (K (x, A₁ ∪ A₂, B₁ ∪ B₂) ≠ ∅)

A2': (B₁ ⊂ A₁ ∧ B₂ ⊂ A₂) → ((K' (x, A₁, B₁) ≠ ∅) ∧ K' (x, A₂, B₂) ≠ ∅) ≡
≡ (K' (x, A₁ ∪ A₂, B₁ ∪ B₂) ≠ ∅)

 

A3: K (x, A, B) ≠ ∅ ≡ (B ⊂ A) ∧ K (x, A, A) ≠ ∅

A3': K' (x, A, B) ≠ ∅ ≡ (B ⊂ A) ∧ K' (x, A, A) ≠ ∅

 

A4: (B₁ ⊂ Ф' ∧ B₂ ⊂ Ф' ∧ B₁ ∩ B₂ = ∅) →
→ K (x, A, B₁) ∩ K (x, A, B₂) ∩ C (x) = ∅

A4': (B₁ ⊂ Ф ∧ B₂ ⊂ Ф ∧ B₁ ∩ B₂ = ∅) →
→ K'(x, A, B₁) ∩ K' (x, A, B₂) ∩ C (x) = ∅

 

A5: ⋀ x ∊ Ф ⋁ y ∊ Ф' (K (x, y, y) ≠ ∅)

A5': ⋀ x ∊ Ф' ⋁ y ∊ Ф (K' (x, y, y) ≠ ∅)

 

A6: K (x, A, B) ∊ ∆ → K (x, A, A ∩ ∼ B) ∊ ∆

A6': K' (x, A, B) ∊ ∆ → K' (x, A, A ∩ ∼ B) ∊ ∆

 

A7: K (x, y, y) ≠ ∅ → K' (y, x, x) ≠ ∅

A7': K' (x, y, y) ≠ ∅ → K (y, x, x) ≠ ∅

 

A8: (x ≠ y) ∧ (v ≠ z) ∧ (K (x, {v, z} v) = K (y, {v, z} v) ≠ ∅ →
→ (K' (v, {x, y}, x) ≠ K' (z, {x, y}, x))

A8': (x ≠ y) ∧ (v ≠ z) ∧ (K' (x, {v, z} v) = K' (y, {v, z} v) ≠ ∅ →
→ (K (v, {x, y}, x) ≠ K (z, {x, y}, x))

 

Vidíme, že nahradíme-li v axiómu neoznačeném čárkou Ф' za Ф, K' za K (a naopak), dostaneme axióm čárkovaný (a naopak). Tato vlastnost, stejně jako podobné rysy různých logických a matematických systémů, může být nazvána dualitou.[15] Symboly Ф a Ф', K a K' budeme pak nazývat symboly navzájem duálními. Ostatní symboly, které takové protějšky nemají (v našem systému např. C), se někdy nazývají samoduální. Principu duality budeme zde využívat zejména v definicích. Ke každému pojmu, který budeme definovat, lze definovat pojem k němu duální, přičemž se tyto definice liší formálně jen tak, že v nich všechny symboly mající duální protějšky těmito protějšky nahradíme.[16]

 

Poznámky k axiómům:

K axiómu 1: Axióm lze přepsat takto, Pro každou formu x a každou dvojici neprázdných množin funkcí A a B platí: jestliže K (x, A, B) je neprázdná množina, je také její průnik s množi[179]nou C (x) neprázdný; dosadíme-li za x -ech, za A množinu deklinačních funkcí této koncovky a za B morfém lok. plur. neutr. subst.,[17] pak K (x, A, B) je množina všech individuálních kontextů charakterizovaných rysem „tvrdý vzor“; u tvrdých vzorů skutečně -ech vyjadřuje lok. plur. neutra nebo jiného rodu s neutrem neutralizovaného, ale nikoli feminina (srov. ránech, masech, kmotrech); průnik množin K (x, A B) a C (x) je tedy neprázdný (existují individuální kontexty společné jim oběma), ale nejde o jejich rovnost ani inkluzi: -ech se vyskytuje i u jiných vzorů (kostech) a tvrdé vzory mají i jiné koncovky.

K axiómu 2: Existuje-li kontext (daný relevantním rysem), v němž určitá forma odpovídá vždy některé ze skupiny funkcí B₁ (a nikoli jiným funkcím ze skupiny A₁), a kontext, kde táž forma odpovídá jedné ze skupiny funkcí B₂ (vybrané z A₂), pak je možno najít i relevantní rys kontextu, v němž tato forma má některou funkci z B (tj. B₁ nebo B₂), nikoli z jiné části A; množina funkcí B je částí množiny funkcí A, v krajním případě se obě shodují, jak ukazuje axióm 3.

K axiómu 4: Tvrdí se tu, že neexistuje homonymie (a duálně synonymie), která by nebyla řešena kontextem, což ovšem v přirozených jazycích platí jen se značnými omezeními; předpokládáme zde, že za relevantní rysy kontextu („vyššího“) lze považovat i určité prvky situace projevu (pro řešení homonymie) a stylu (pro řešení synonymie).

K axiómu 5: Zde se v podstatě tvrdí, že ke každé formě existuje funkce, která je jí vyjádřena (a — podle duálního axiómu — také naopak).

K axiómu 6: Předpokládáme, že množinu všech relevantních rysů kontextů lze rozdělit na kontexty „vyšší“ a „nižší“ vzhledem k rovině toho kterého vztahu; např. pro vztah morfu k morfému je nižším kontextem jak kontext fonologický, tak i kontext z roviny morfů, kdežto ty rysy kontextu, kde se počítá s prvky funkce morfémů (slovní druh, rod atd.), patří už ke kontextu vyššímu; pro vztah fonému k hlásce (funkce k formě) počítáme fonologické rysy ke kontextu nižšímu. V systému nižších kontextů, označovaném zde jako Δ, jsou tedy zahrnuty i kontexty stejnorodé, obsahující i prvky z roviny Φ. Členění kontextu je pro bližší zkoumání složitých vztahů funkce a formy problémem velmi závažným; pro zevrubnější třídění bude třeba rozlišovat tu především mezi kontextovými rysy systémovými (fonologickými, morfologickými, syntaktickými) a mezi rozmanitými rysy jednotlivými, kdy je množina určena soupisem slovních kmenů ap. (zejm. v kontextu lexikálním a v situaci promluvy). Axiómy 6 a 6' tvrdí jen tolik, že kontextové měřítko pro výběr z dvou množin funkcí nebo forem patří celé do nižšího kontextu, patří-li tam jedna z obou složek: např. v lok. plur. neutr. subst. je měřítko pro užití koncovky -ech z nižšího kontextu (tvrdý kmen, nekončící na -k, -g, -ch, -h, kromě les ap.), takže poznáme už z tohoto kontextu, kdy vůbec přichází v úvahu dvojice koncovek -ích, -ách. Složitost členění kontextu si právě vynucuje, že naše soustava axiómů i výchozí pojmy nemohou být nahrazeny jednoduššími.

K axiómu 7: Axióm tvrdí v podstatě toto: Jestliže forma x vyjadřuje v některém kontextu funkci y, pak je funkce y v některém kontextu vyjadřována formou x. Tyto kontexty však nebudou obecně shodné: při postupu od formy k funkci jsou často relevantní jiná kontextová měřítka než při postupu od funkce k formě, neboť se vybírá z různých množin A, B (např. abychom poznali, zda koncovka -í vyjadřuje nom. plur. živ. adj., nebo gen. plur. fem. subst., musíme vědět, k jakému slovnímu druhu náleží kmen, s kterým je spojena; naproti tomu pro přiřazení formy -í funkci gen. plur. subst. fem. stačí vědět, že jde o kmen určitého paradigmatu: nůše, píseň, kost, nikoli žena, ulice, chvíle).

K axiómu 8: Tento axióm se týká rozdělení jazykových jednotek do různých rovin; k jeho úloze v našem systému srov. odst. 5.

Pro uvedený systém axiómů lze nalézt i interpretace nelingvistické; při studiu vztahu funkce a formy by patrně bylo možno pracovat se systémem silnějším, který by výchozí pojmy charakte[180]rizoval úplněji. Zůstáváme tu u systému slabšího, protože způsob zesílení axiómů (nebo formulace dalších) bude záviset na výsledcích, k nimž se dojde rozborem vztahů mezi jednotkami vyšších rovin jazykového systému.

4. Z našeho systému axiómů lze vyvodit toto tvrzení: Ke každé formě x existuje právě jedna neprázdná množina funkcí A taková, že pro všechny množiny funkcí B z toho, že A je podmnožinou B a z neprázdnosti množiny K (x, B, B) plyne rovnost množin A a B. Tuto množinu A nazveme α x; je to tedy množina všech funkcí vyjadřovaných formou x. Duálně k tomu lze vyslovit toto tvrzení: Ke každé funkci x existuje právě jedna neprázdná množina forem A taková, že pro všechny množiny forem B z toho, že A je podmnožinou B a z neprázdnosti množiny K'(x, B, B) plyne rovnost množin A a B. Tuto množinu A nazveme α'x; je to tedy množina všech forem vyjadřujících funkci x.

Další tvrzení zapíšeme symbolicky (v této podobě totiž je logická stavba výroku přehlednější a jasněji vynikne vztah mezi výroky navzájem duálními):

⋀ x ∊ Φ ⋁ y ∊ Φ' (K (x, αx, y) ≠ ∅)

a duálně k tomu:

⋀ x ∊ Φ' ⋁ y ∊ Φ (K' (x, α'x, y) ≠ ∅)

To znamená, že ke každé formě existuje nějaká funkce, kterou vyjadřuje, a naopak.

Dále uvedeme čtyři definice:

D1': Q (x, A) = _dfK (x, αx, A)

D1': Q' (x, A) = _dfK' (x, α'x, A)

Q (x, A) je množina individuálních kontextů, v nichž x vyjadřuje funkce z množiny A; Q' (x, A) je k ní duální.

D2: R (x, y) ≡ _df(x ∊ Φ) ∧ (y ∊ Φ') ∧ (K(x, y) ≠ ∅)

D2': R' (x, y) ≡ _df(x ∊ Φ') ∧ (y ∊ Φ) ∧ (K'(x, y) ≠ ∅)

Definujeme zde relace „forma x vyjadřuje funkci y“ a „funkce x je vyjadřována formou y“. Vyšli jsme ze složitých pojmů a docházíme nyní k pojmům jednodušším, nepoměrně názornějším, což je pro námi zvolený postup charakteristické. O relacích R a R' platí toto jednoduché tvrzení:

⋀ x ∊ ⋁ y ∊ Φ' (R (x, y))

a duálně:

⋀ x ∊ Φ' ⋁ y ∊ Φ (R' (x, y))

Snadno se lze přesvědčit, že R' (x, y) platí právě tehdy, platí-li R (y, x).

Na definicích Dl — D2' (a také na tvrzeních, zejména zapisujeme-li je symbolicky) je vidět dualitu našeho systému. Napříště nebudeme vždy uvádět duální protějšky definic, neboť v tom, že lze explicite definovat jen polovičku a druhá polovička je definována mlčky s sebou, záleží výhoda tohoto duálního systému. Duální definice budeme uvádět jen tehdy, budeme-li pro duální pojem zavádět odlišné jméno nebo znak, jak tomu bude v těchto definicích:[18]

[181]D3: syn (x, y) ≡ _df (x ∊ Φ) ∧ (y ∊ Φ) ∧ (α x = α y)

D3': hom (x, y) ≡ _df (x ∊ Φ') ∧ (y ∊ Φ') ∧ (α' x = α' y)

 

D4: semisyn (x, y) ≡ _df (x ∊ Φ) ∧ (y ∊ Φ) ∧ (α x ∩ α y ≠ ∅)

D4': semihom (x, y) ≡ _df (x ∊ Φ') ∧ (y ∊ Φ') ∧ (α' x ∩ α' y ≠ ∅)

 

D5: Syn (x) = _df Ԑ y ∊ Φ (syn (x, y))

D5': Hom (x) = _df Ԑ y ∊ Φ' (hom (x, y))

 

D6: Semisyn (x) = _df Ԑ y ∊ Φ (semisyn (x, y)); pro x ∊ Φ

D6': Semihom (x) = _df Ԑ y ∊ Φ' (semihom (x, y)); pro x ∊ Φ'

 

První čtyři definice vymezují relace, ostatní množiny. Relace syn, hom, semisyn, semihom budeme číst jako „jsou synonymní“, „jsou homonymní“, „jsou semisynonymní“ a „jsou semihomonymní“; tedy např. formy x a y jsou synonymní, když všechny funkce, které vyjadřuje forma x, vyjadřuje i forma y a naopak; dále např. Semisyn (x) je množina všech forem, které vyjadřují alespoň jednu společnou funkci s formou x.

Relace syn je reflexívní, symetrická a tranzitivní na Φ;[19] to znamená, že předpis Syn (který každé formě přiřazuje množinu forem) vytváří na Φ disjunktní rozklad.[20] Dále je zřejmé, že pro libovolné formy x a y platí

syn (x, y) → semisyn (x, y)

a

Syn (x) ⊂ Semisyn (x)

 

Obdobně lze charakterizovat pojmy, které jsou k výše uvedeným duální (např. relace hom je reflexívní, symetrická a tranzitivní na Φ' atd.).

Protože vztah syn je alespoň v některých rovinách jazykového systému poměrně vzácný, je lépe při popisu vycházet ze zobrazení Semisyn. To sice obecně disjunktní rozklad na Φ nedefinuje (není tranzitivní; jazyková jednotka může být semisynonymní s několika jinými, mezi nimiž takový vztah není), ale můžeme na jeho základě k takovému rozkladu dospět těmito definicemi vztahu sd_s (čteme „jsou synonymně sdruženy“) a množiny synonymně sdružených prvků Sd_s (N označuje v této definici množinu celých kladných čísel):

D7: sd_s (x, y) ≡ _df (x ∊ Φ) ∧ (y ∊ Φ) ∧⋁ n ∊ N ⋁ x₁ ∊ Φ … ⋁x_n–1 ∊ Φ
(semisyn (x₀, x₁) ∧ … ∧ semisyn (x_n–1, x_n) ∧ (x_n = y) ∧ (x₀ = x))

D8: Sd_s (x) = _df Ԑ y ∊ Φ (sd_s (x, y)); pro x ∊ Φ

Pojmy duální k právě definovaným můžeme označit sd_h (čteme (jsou homonymně sdruženy“) a Sd_h.

[182]Definice D7 má dosti složitou strukturu. Proto ji přepíšeme v přirozeném jazyce: dvě formy x a y jsou synonymně sdružené, když existují formy x₀, x₁ …, x_n–1, x_n — kde n je celé kladné číslo — takové, že 1) x = x₀, y = x_n; 2) platí zároveň semisyn (x₀, x₁), …, semisyn (x_n–1, x_n).

Relace sd_s je reflexívní, symetrická a tranzitivní na Φ; to znamená, že předpis Sd_s (který každé formě přiřazuje množinu forem) vytváří na Φ disjunktní rozklad. Dále je zřejmé, že platí-li pro formy x a y semisyn (x, y), platí též sd_s (x, y); pro každou formu x je Semisyn (x) podmnožinou množiny Sd_s (x). O vztahu mezi relacemi sd_s a sd_h platí: je-li funkce v vyjádřena formou x a funkce w formou y, potom: sd_s (x, y) → sd_h (v, w). Obdobně lze charakterizovat i pojmy, které jsou k pojmům výše uvedeným duální.

Vezmeme-li jako příklad podsystém plurálových koncovek české deklinace,[21] můžeme tedy podoby deklinačních morfémů (morfy) rozdělit do několika skupin forem synonymně sdružených a jejich funkce do odpovídajících skupin funkcí homonymně sdružených. Ve shodě s obvyklým postupem považujeme zatím jednotlivé morfy (podoby koncovek) za formy a jednotlivé morfémy za jejich funkce, ačkoli tento postup není jediný možný, jak ještě uvidíme. Protože např. platí semisyn (ové, ’i),[22] semisyn (’i, i), semisyn (i, mi), platí i sd_s (ové, mi), ačkoli tyto dvě formy žádnou společnou funkci nemají. Předpis Sd_s definuje na množině českých plurálových deklinačních koncovek tento rozklad:

1. é, ové, ’i, i, e, a, mi, emi, ami

2. á

3. í, ∅

4. ů

5. ch

6. s

7. ům, ím, em, ám

8. ách, ích, ech

Při rozkladu na prvky synonymní bychom dostali místo první podmnožiny ještě rozdělení na {é, ové}, {’i}, {i}, {e}, {a}, {mi}, {emi, ami}, také podmnožiny 3. a 7. by byly ještě dále rozděleny a jen 8. podmnožina by i pak měla tři členy.

Pro stejný podsystém dostaneme rozklad morfémů na podmnožiny prvků homonymně sdružených:

1. nom. živ. subst., ak. neutr. subst., ak. fem. subst., instr. fem. subst., instr. neutr. subst.

2. ak. neutr. adj.

3. nom. živ. adj., ak. fem. adj., gen. fem. subst.

4. gen. neživ. subst.

5. gen. fem. adj.

6. gen. bezrod. zájm.

7. dat. neživ. subst., dat. neutr. subst., dat. fem. subst.

8. lok. neutr. subst., lok. fem. subst.

[183]V dalším budeme užívat tohoto příkladu jako ukázky, jak by mohl být s použitím našeho aparátu popsán celý systém dané roviny; kromě toho budeme uvádět jednotlivé příklady z jiných podsystémů (pro jiné roviny nebo pokud půjde o vztahy v našem podsystému nezastoupené).

Na základě uvedených vztahů je možno definovat pojem (kombinatorních) variant:

D9: var (A, B; x) ≡ _df (A ⊂ Φ) ∧ (B ⊂ Φ) ∧ (A ≠ ∅) ∧ (B ≠ ∅) ∧
∧ ⋀ v ∊ A ⋀ w ∊ B (((x ∊ (α v ∩α w))∧ (K' (x, A ∪ B, A) ∊ Δ))

Tuto symbolicky zapsanou relaci můžeme číst „A a B jsou (kombinatorní) varianty vzhledem k x“. Pracujeme tu s množinami — A a B —, nejen s prvky, neboť vztah kombinatorních variant neplatí vždy pro dvě jednotlivé koncovky; např. vzhledem k lok. plur. neutr. subst. jsou kombinatorními variantami na jedné straně -ech a na druhé straně celá dvojice -ích, -ách: nižším kontextem (paradigmatem kmenu a hláskoslovně) je dáno, zda užijeme první z variant (po tvrdém kmenu nekončícím na k, g, ch, h, kromě les ap.),[23] nebo druhé; v rámci této druhé varianty je však už výběr mezi koncovkami -ích a -ách zčásti dán stylisticky. Vztah var (A, B; x) je při konstantním x reflexívní, symetrický a tranzitivní, takže příslušný předpis Var definuje na Φ disjunktní rozklad. Protože kromě výše uvedené výjimky jsou v našem příkladu všechny varianty podmnožinami o jednom prvku, můžeme je přehledně zachytit takto:[24]

Var (é; nom. živ. subst.) = {e, ové}

Var (i; ak. fem. subst.) = {i, ’i, e}

Var (a; ak. neutr. subst.) = {a, e}

Var (∅; gen. fem. subst.) = {∅, í}

Var (ům; dat. neutr. subst.) = {ům, ím}

Var (ám; dat. fem. subst.) = {ám, ím, em}

Var (ách; lok. fem. subst.) = {ách, ích, ech}

Var (ami; instr. fem. subst.) = {ami, emi, mi}

Var (i; instr. neutr. subst.) = {i, mi}

 

V rovině fonologické bude ovšem pro češtinu platit např.:

 

Var (n; /n/) = {n, η}

Var (d; /d/) = {d, t}

 

V staré řečtině, kde η (psané γ) je jak variantou fonému n (před velárou), tak i fonému /g/ (před n, m),[25] platí:

 

Var (n; /n/) = {n, η}

Var (g; /g/) = {g, η}

Tyto různé dvojice nebo trojice variant se mezi sebou liší především v jednom ohledu: buď má každá z nich jen tu funkci, vůči níž je variantou druhé, nebo[184]má některá také funkci jinou.[26] Definujeme-li relaci mon (x) („x je monofunkční“) takto:[27]

D10: mon (x) ≡ _df (x ∊ Φ) ∧ ⋁ ! y ∊ Φ' (R (x, y))

můžeme jednak předem vyřadit z dalšího probírání ty prvky x, y, pro které platí R (x, y) a zároveň mon (x) i mon' (y), protože nejsou v našem systému nijak spojeny s jinými prvky z obou rovin, a dále můžeme výhodně rozdělit víceprvkové množiny variant na ty, kde všechny prvky splňují podmínku mon (x), jako např. dvojice n, η nebo é, ové v češtině, a na ty, kde tato podmínka pro všechny členy splněna není, jako např. d, t; řec. n, η; ách, ích, ech.[28]

Platí-li var (A, B; x) a zároveň pro každou formu y z A i B platí mon (y), pak jsou A, B uvnitř své roviny tímto vztahem (z hlediska našeho systému) plně charakterizovány a můžeme hledat další zajímavé vztahy jen uvnitř A nebo B (podmnožiny jedné z nich mohou být stylistickými variantami ap.). Avšak neplatí-li mon (y) pro všechny prvky variant, má smysl se ptát po dalších podmínkách, především po tom, jaké kontextové měřítko řeší (semi)homonymii u toho (těch) y, pro které neplatí mon (y). Je-li také toto měřítko prvkem systému Δ, pak je v daném případě vztah variant oboustranný a v α y existuje alespoň jeden prvek, který je s x v relaci duální k var (A, B; x) z D9. Tuto relaci můžeme číst ,,A a B jsou variační funkce (vzhledem k formě) y“.

Z plurálu české deklinace můžeme uvést příklad: var' (lok. fem. subst., lok. neutr. subst.; ech); z příkladů hláskoslovných sem patří var' (/n/, /g/; η) v řečtině; z jiných oblastí lze uvést: var' (1. os. sing., 1. os. pl.; -m); var' (přísudkové jméno, činitel; instr.) a podobně pro další funkce instrumentálu a jiných pádů, pokud jsou jednoznačně rozlišeny slovesem nebo jeho tvarem, předložkou ap.

Je-li naopak kontextové měřítko při homonymii vzato z vyššího kontextu (tj. kontext není prvkem Δ), pak se budeme ptát, zda B obsahuje prvek „konexní“ s některým prvkem množiny A; za konexní — kon — přitom považujeme ty prvky, které se liší právě jedním ze svých distinktivních či sémantických rysů (tj. dva fonémy lišící se jedním distinktivním rysem, dva morfémy lišící se jedním sématem). Tak dospíváme ke vztahu neutralizace,[29] který můžeme definovat takto:

D11: neut (x, y; z, v) ≡ _df x ∊ Φ' ∧ y ∊ Φ' ∧ z ∊ Φ ∧ v ∊ Φ ∧ kon (x, y)
∧ (z ≠ v) ∧ K' (x, {v, z}, z) ∊ Δ ∧ ~ (K (z, {x, y}, x) ∊ Δ)

Bereme tu v úvahu jen prvky, ačkoli by bylo přesnější i zde vycházet ze vztahu mezi množinami; pro popis našich příkladů to však není nutné. Vztah, který tu nazýváme neutralizací, bývá označován jako neutralizace syntagmatická, na rozdíl od neutralizace paradigmatické (srov. výše pozn. 21). Otázky paradigmatické neutralizace jsou těsně spojeny s problematikou struktury jednotek té které roviny, takže je nelze řešit jen v rámci tohoto systému, soustředěného na [185]vztah mezi dvěma rovinami, neboť jednotky formy i funkce tu považujeme za prvky a jejich složení nezkoumáme. Výjimku jsme učinili v jistém smyslu u pojmu konexního vztahu, který však je v této práci z právě uvedených příčin jen na okraji. Podle toho, jak jsme vztah konexity předběžně vymezili, můžeme hledat vztah neutralizace jen u těch rovin, kde funkce mají strukturu podobnou jako fonémy nebo morfémy. Jako příklady neutralizace můžeme tedy uvést: neut (nom. živ. jmen. adj., nom. živ. slož adj., í, ’i) u adjektiv, která nemají zvláštní formu pro jmenné tvary a kde tedy složené tvary plní i tuto funkci, dále neut (ak. plur. jmen. fem. adj., ak. plur. fem. slož. adj.; ∅, i); kromě toho sem patří (syntagmatické) neutralizace fonologické a můžeme sem zařadit také např. paradigmatické neutralizace v deklinaci, považujeme-li sémata slovního druhu a rodu u substantiv jen za rysy kontextu, ne za sémata koncovek.

Jako příklady vztahu k neutralizaci duálního můžeme z rovin dosud zpracovaných uvést jen jednotlivé případy, do značné míry osamocené, jako: neut’ (pádel, vesel; „veslo“).

Nepočítáme-li totiž s knižním, až archaickým jmenným tvarem vesel od adjektiva veselý, platí tu skutečně podmínky pro kontexty (kontextové měřítko pro řešení synonymie je z vyššího kontextu, totiž stylistické, a měřítko pro řešení homonymie u morfu vesel- je z kontextu nižšího: jde o kmen substantiva veslo, následuje-li nulová koncovka, jinak o kmen adjektiva) a morfy pádel, vesel jsou si podobné, což je vztah, který předběžně považujeme za duální ke vztahu konexity. Za podobné považujeme dvě jednotky shodující se v těch svých členech (či v těch jejich prvcích), jichž se týká nějaká alternace v paradigmatu; označíme tento vztah pod a budeme tedy psát pod (ran, sil), pod (matc, noz) atd.

Vztahy podobnosti a konexity jsou ovšem jen předběžně vybrány z většího množství vztahů mezi jednotkami téže roviny, které bude možno plněji zpracovat teprve tehdy, až systém náš nebo podobný obsáhne vedle vztahů mezi jednotlivými rovinami strukturní vztahy jednotek uvnitř téže roviny. Značnou nevýhodou pro nás je také to, že oba tyto vztahy platí, jak už uvedeno, jen pro jednotky některých rovin a že nemáme zatím nic, co by jim odpovídalo v rovinách jiných. Toto vnější omezení našeho systému by bylo možno celkem snadno odstranit např. tím, že bychom nepracovali se vztahem neutralizace, nýbrž s obecnějším vztahem, vymezeným bez ohledu na konexitu (a — duálně — na podobnost). Pak bychom za dvojice splňující tento vztah (můžeme jim říkat třeba prvky synkretické) považovali všechny, které splňují tuto definici:

D12: synkr (x, y; w, z) ≡ _df (x ∊ Φ') ∧ (y ∊ Φ') ∧ (w ∊ Φ) ∧ (z ∊ Φ)
∧ (x ≠ y) ∧ (w ≠ z) ∧ K' (x, {w, z}, w) ∊ Δ ∧ ~ (K (w, {x, y}, x) ∊ Δ)

tedy — kromě výše uvedených, které splňují vztah neutralizace — také např. kmeny slov dělo a dílo, spojené morfémem děl (před nulovou koncovkou), nebo deklinační morfémy ak. plur. neutr. subst. a ak. plur. fem. subst., spojené morfem -e. Duální k tomuto vztahu je např. vztah koncovek -í a ∅ vůči gen. plur. fem. a ak. plur. adj.

O posledních dvou vztazích platí toto tvrzení:

synkr (x, y; w, z) → ~ synkr' (w, z; x, y)

Konečně můžeme definovat ještě vztah fundace, formulovaný J. Kuryłowiczem;[30] vzhledem k tomu, že i tento vztah, podobně jako neutralizace, je vázán [186]vlastnostmi struktury jednotek dané roviny, definujeme tu formálně jen jeho podklad, společný jednotkám všech rovin, k němuž pak přistupují další rysy (zejm. podobnost, popř. konexita mezi y a v):

D13: fund (x, y; z) ≡ _df (x ∊ Φ) ∧ (y ∊ Φ) ∧ (z ∊ (α x ∩ α y)) ∧ ⋁ v ∊ Φ ⋁ w ∊ Φ'
((Q' (z, y) ⫋ Q' (w, v)) ∧ (Q' (w, v) ∩ Q' (z, x) ∩ C (x) ∩ C (v) ≠ ∅)) ∧
⋀ u ∊ Φ ⋀ t ∊ Φ' (u ≠ v → ~ ((Q' (z, x) ⫋ Q' (t, u)) ∧
∧ (Q' (t, u) ∩ Q' (z, y) ∩ C (y) ∩ C (u) ≠ ∅)

Jako příklady uvádíme: fund (ách, ích; lok. plur. neživ. subst.) — srov. -u v lok. sing.; fund (honos, honor-, „honos“) — srov. auctor; fund (pusť-, pušč-; „pustit'“) — srov. soobšč-; pro ruské varianty fonému /i/ platí fund (i, y; /i/).

5. Počítali jsme dosud s tím, že máme předem dáno rozdělení jazykových prvků do rovin[31] a že tedy víme, který prvek může být funkcí jiného (tj. který prvek je členem množiny Φ a který je členem množiny Φ'). Je však v souhlasu s naším systémem takové rozdělení rovin, jaké se obvykle předpokládá, tj. rozdělení prvků na hlásky, fonémy, morfémy a dále na jednotky syntaktické? Jinak řečeno, je z hlediska našeho systému vztah hlásky k fonému stejným vztahem formy a funkce jako vztah morfu k funkci morfému (tedy např. vztah -ům k funkci „dat. pl. neživ. subst.“) atd.? (Srov. otázky I. a III. na s. 175.)

Tohoto rozdělení prvků do rovin se týká v našem systému axióm 8, který především zajišťuje, že nebudeme vidět bezprostřední vztah formy a funkce mezi jednotkami vzdálených jazykových rovin. Nemůžeme např. považovat hlásku -l[32] za přímé vyjádření minulosti v určitém kontextu, neboť síť vztahů, kterou bychom s použitím našeho aparátu sestavili, by obsahovala mimo jiné tyto relace:

K (l, A, min.) = K (l̥, A min.)

K' (min., B, l) = K' (kondic., B, l)

kde A je množina morfologických funkcí zahrnující min a kondic[33] a B je množina hlásek zahrnující l (např. v kupoval) a slabičné l̥ (např. v tvaru vedl). Uvedené rovnice však zcela zjevně nevyhovují axiómu 8, takže v rámci našeho systému musíme dané vztahy vyjádřit jinak. Především nebudeme uvádět do přímého vztahu k morfologickým jednotkám hlásky, neboť jejich kontextové rozdělení, pokud je dáno měřítky typu Q' (/l/, l) ∊ Δ, je z hlediska vyšších rovin (morfologie atd.) irelevantní, hlásky samy nejsou funkčními jednotkami jazyka. [187]Budeme tedy hlásky l a l̥ považovat za varianty jedné jednotky, fonému /l/. K těmto zjištěním se došlo už v začátcích moderní lingvistiky. Je však dosud nejasno o podobných vztazích uvnitř morfologie; budeme-li i zde vyžadovat platnost uvedeného axiómu, který potvrzuje existenci zvláštní roviny fonémů, uvidíme, že se ani tady nevystačí s jednoduchým vztahem mezi dvěma rovinami (srov. podoby koncovek a gramatické významy v našich mluvnicích, morfy či allomorfy a morfémy deskriptivní lingvistiky ap.).

Vyjděme od vztahů R (/l/, min) a R (/l/, kondic.), kde /l/ už označuje morf tvořený fonémem, nikoli hláskou; pak by platilo, přibereme-li např. hovorové tvary typu ved, sed si:

Q (l, min.) = Q (0, min) a zároveň

Q' (min, l) = Q' (kondic, l),

to je opět v rozporu s uvedeným axiómem. Musíme tedy předpokládat ještě další rovinu s jednotkou, kterou označíme zatím λ (můžeme jí říkat l-forma nebo podobně),[34] pro kterou platí:

R (0, λ) i R (λ, kondic.)

R (l, λ) i R (λ, min.)

To už naší soustavě axiómů plně vyhovuje.

Domníváme se, že takový postup spojený s vyčleňováním nových jednotek (s diferenciací, dělením pojmů tradičních)[35] je v souladu s postupem dosud v lingvistice obvyklým, jak je zřejmé z příkladu fonologie a jak by se dalo ukázat také na jednotlivých ukázkách z morfologie aj. Jako nové jednotky se tu vyčleňují takové, vůči kterým pak jednotky dosavadní vystupují jako varianty, variační funkce (např. min. a kondic. vůči λ) nebo prostě jako jejich (semi)synonymní formy, popř. (semi)homonymní funkce.

Zvolili jsme axióm 8 pokud možno slabý, tak aby vedl k vyčleňování nových jednotek jen tam, kde je to oprávněné a kde to znamená zjednodušení popisu. Uvedený příklad však naznačuje, že takové vyčlenění nových jednotek patrně bude namístě i tam, kde se nepředpokládalo (srov. s. 182 o vztahu mezi podobami koncovek a morfémy). Takové vyčlenění jednotky ovšem předpokládá v našem systému vytvoření celé nové roviny.

Náš systém však neurčuje kritérium, podle kterého by takové roviny (jako např. nová rovina mezi podobami a funkcemi morfémů, k níž náleží λ) mohly být jednoznačně doplněny. Pro další postup je tu tedy několik možností, zejména: a) oslabit dále systém axiómů tak, aby nepředpokládal „úplnost rovin“ (srov. otázku II. na s. 175), nebo

b) doplnit potřebné kritérium podle struktury jednotek té které roviny, podle jejich paradigmatických neutralizací a jiných vztahů (srov. otázku V.).

6. Dualita v našem systému není taková, jakou v jazyce předpokládá G. Herdan (srov. pozn. 15). Jeho srovnání jazykového systému s projektivní geometrií, zejména s projektivní geometrií roviny, je příliš přímočaré. Nedostatkem je, že autor postuluje všeobsáhlou shodu obou těchto systémů, [188]ale nepodává konkrétní zpracování těchto otázek, dokonce ani neukazuje příklad jednoduchého podsystému z některé jazykové roviny, který by jeho předpokladům vyhovoval. Při snaze takový příklad najít by bylo možno uvést dílčí soustavy tohoto typu:

 

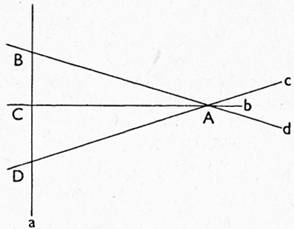
a) Duální vztah foném-morf:

Považujeme tu fonémy za body (A : /e/, B : /v/, C : /l/, D : /k/) a morfy za přímky (a : vlk, b : len, c : keř, d : ves). V takové soustavě by platilo: dvě přímky se protínají — dva morfy mají společný foném; dva body leží na téže přímce — dva fonémy jsou v témž morfu.

Hned by se však ukázalo, že jde jen o skupinu prvků vybranou ad hoc, která není typická pro jazykový systém. Snadno se totiž dají uvést příklady mj. na dvojice morfů, které mají víc než jeden foném společný, a naopak na dvojice fonémů, které se vyskytují ve více morfech.

b) Duální vztah morf-morfém:

Zde považujeme morfy za body (A : -en, B : -e, C : -es, D : -er) a morfémy za přímky (a : nom. sing., b : gen. sing., c : gen. plur., d : nom. plur. — jak je zřejmé, jde o vybrané koncovky německé silné a slabé deklinace). Pak by platilo: každé dvě přímky se protínají v jednom bodě — každé dva morfémy mají jeden společný morf; každé dva body leží společně na jediné přímce — každé dva morfy mají jeden společný morfém.

Jakmile však přihlédneme k rodu, k dalším funkcím uvedených morfů atd., zjistíme snadno, že situace není tak jednoduchá.

Můžeme stručně říci, že vztah formy a funkce zdaleka neodpovídá vztahu bodu a přímky v projektivní geometrii roviny už proto, že zdaleka vždy není dvěma funkcím přiřazena jedna společná forma a dvěma formám jedna společná funkce. Podobně to platí i o jiných vztazích uvnitř jazykového systému.

Snažili jsme se ukázat, že formalizace vztahu funkce a formy v jazyce může přispět k utřídění lingvistických pojmů z této oblasti, ačkoli systém, jaký jsme tu mohli předložit, pro úplné zpracování nestačí. I když dualita vztahu formy a funkce není tak bohatá jako např. dualita projektivní geometrie, domníváme se, že je to pojem plodný, jehož prostřednictvím můžeme od důležitých jazykových vztahů v lingvistice už zjištěných dojít ke vztahům duálním. Takový postup bude mít svůj význam pro studium vztahu syntézy a analýzy (přístupu k jazyku „z hlediska mluvčího“ a „z hlediska posluchače“) a pro srovnávání různých rovin jazykového systému.[36] Vzhledem k tomu, že tyto roviny nejsou ve stejné míře [189]přístupné objektivnímu zkoumání, bude, jak se zdá, výhodné, se zřetelem k dualitě formy a funkce předběžně usuzovat na některé vlastnosti vyšších rovin podle známých vlastností rovin nižších a výsledky pak empiricky ověřovat.

 

R é s u m é

ОТНОШЕНИЕ ФОРМЫ И ФУНКЦИИ В ЯЗЫКЕ

Цель статьи — построить аксиоматическую систему, которая могла бы служить аппаратом описания отношения «формы» и «функции» на разных уровнях языка. Исходными понятиями являются: Ф и Ф' (множество форм и их функций), С (х) (множество всех индивидуальных контекстов, в которых встречается форма или функция х), K (х, А, В), где х ɛ Ф, А ⊂ Ф', В ⊂ Ф', А ≠ ∅, В ≠ ∅ (множество индивидуальных контекстов — определенное признаком — в которых форма х в множестве функций A «выражает» только некоторую функцию из множества В; так напр. в русском языке K (-ю, падежные функции -ю, твор. пад. ед. ч. сущ. ж. р.) можно определить признаком «основы типа кость»; задается также система контекстов Δ [формула K (х, А, В) ɛ Δ означает, что признак контекста основан на единицах того же плана языка, к которому принадлежит х или на единицах более низкого плана].

На этой основе в статье строится аксиоматическая система (см. абз. 3), особенностью которой является принцип двойственности; двойственность в языке здесь понимается уже, чем в работах Г. Гердана (см. абз. 6). В абз. 4 даются определения лингвистических понятий синонимии (и двойственной к ней омонимии), семисинонимии (семиомонимии), элементов синонимически (омонимически) сближенных (Sd_s и Sd_h), вариантов (вариационных функций), нейтрализации, более общего отношения «синкретических» элемеитов и фундации. В абз. 5 намечены возможности применения такой системы к решению вопросов, касающихся распределения единиц языка по разным планам.

Slovo a slovesnost, volume 23 (1962), number 3, pp. 174-189

Previous Jan Firbas: Ze srovnávacích studií slovosledných (K Mathesiovu pojetí slovosledné soustavy)

Next Karel Hausenblas: Styly jazykových projevů a rozvrstvení jazyka (K diskusi o obecné a hovorové češtině)