Nové práce N. Chomského a G. A. Millera v příručce matematické psychologie

Pavel Novák, Karel Pala, Miluše Sedláková

[Discussion]

(pdf)

Новая работа H. Хомского и Дж. А. Миллера в учебнике математической психологии / Nouveaux travaux de N. Chomsky et G. A. Miller dans le manuel de la psychologie mathématique

1. Po starší už americké příručce experimentální psychologie[1] následuje příručka psychologie matematické. První vydání třísvazkového díla Handbook of mathematical psychology (eds. R. Luce, R. Bush a E. Galanter) je u konce. Svazek 1, obsahující 1. až 8. kapitolu, vyšel r. 1963, svazek 2, s 9. až 14. kapitolou, r. 1964, a svazek 3, s 15. až 21. kapitolou, r. 1965.

Dílo je určeno pro čtenáře s jistými znalostmi tzv. konečné matematiky, matematické analýzy, teorie pravděpodobnosti a matematické statistiky. Žádanou úroveň lze posoudit podle toho, že se pro oblast první uvádí např. J. G. Kemeny - J. L. [72]Snell - G. L. Thompson, Introduction to finite mathematics (Englewood Cliffs 1957) a pro oblast třetí W. Feller, An introduction to probability theory and its applications (New York 1957).[2]

Užším otázkám psychologickým je věnováno 13 kapitol (např. různým otázkám psychofyzickým, matematické teorii učení).[3] O třech kapitolách pro lingvisty nejzajímavějších viz zde dále podrobněji. V této souvislosti připomeňme i 15. kap.: J. Zwislocki, Analysis of some auditory characteristics.

Do příručky jsou však zařazeny i dvě kapitoly obecně metodologické a dvě matematické: 1. P. Suppes - J. L. Zinnes, Basic measurement theory (Základy teorie měření), 8. R. R. Bush, Estimation and evaluation (Odhad a ohodnocení), 20. J. L. Snell, Stochastic processes a 21. R. Bellman, Functional equations (Funkcionální rovnice).

Kapitola 1. je nejlepší úvod do obecné teorie základního měření (fundamental) i odvozeného (derived), který vůbec existuje.[4] V obou případech autoři vždy kladou a exaktně řeší otázku zdůvodnění (justification) přiřazení čísel objektům nebo jevům a otázku specifikace stupně, v jakém je toto přiřazení jednoznačně dáno. Příklady jsou přirozeně vzaty z psychologie. Výsledků a podnětů této práce by mohli s výhodou použít badatelé v oblasti jazykové typologie a stylistiky.[5]

V kapitole 8. autor odlišuje otázku ohodnocení (modelu) od otázky testování hypotéz,[6] neboť „tovární výrobky … mohou být přijaty nebo zamítnuty, avšak formální teorie jsou hodnoceny, modifikovány a rozšiřovány“ (s. 432).

Příručka je provázena dvousvazkovou čítankou (Readings in mathematical psychology).

Pavel Novák

 

2. Kapitoly lingvisticky nejzajímavější jsou umístěny ve svazku 2 a obsahují práce N. Chomského a G. A. Millera. Jsou to: kap. 11 (s. 270—321) — N. Chomsky - G. A. Miller, Úvod do formální analýzy přirozených jazyků; kap. 12 (s. 324—418) — N. Chomsky, Formální vlastnosti gramatik; kap. 13 (s. 419—491) a G. A. Miller - N. Chomsky, Konečné modely uživatelů jazyka. Zařazení těchto kapitol do psychologické příručky je zcela organické, jak dále ukážeme. Příručka sama je zejména po metodologické stránce velmi cenným zdrojem poznatků i pro lingvisty.

3. Kapitola Úvod do formální analýzy přirozených jazyků je věnována základní lingvistické problematice, vysvětlují se v ní základní pojmy algebraické lingvistiky. Podle Chomského a Millera (dále jen Ch., M.) každé zkoumání jazyka a jazykového chování se musí vyrovnat s tou základní skutečností, že mluvčí má schopnost v mateřském jazyce chápat veliký počet vět, které předtím nikdy neslyšel, a produkovat při vhodné příležitosti nové věty, které jsou srozumitelné všem ostatním příslušníkům téhož jazyka. To vede k položení tří základních otázek: 1. Jaká je povaha této schopnosti? 2. Jak se jí užívá? 3. Jak se osvojuje?

Zodpovědět první otázku znamená objasnit strukturu vlastní všem přirozeným jazykům. O zásadní řešení této otázky se pokoušejí logika a lingvistika a soustřeďují se v poslední době na pojem gramatiky. Odpovědět na druhou otázku vyžaduje pokus podat formální charakteristiku nebo model uživatele jazyka. Odpověď na třetí otázku [73]je neméně důležitá, ale postihnout proces osvojování mateřského jazyka u dítěte je zatím mimo možnosti matematických modelů.[7]

Pozornost autorů je v uvedených kapitolách soustředěna na formální studium přirozených jazyků a jejich syntaktických problémů s cílem důkladně připravit půdu i pro studium problémů sémantických.[8] Umělé jazyky se ponechávají stranou a užívá se jich jen k ilustrování některých konkrétních formálních vlastností jazyka.

Komunikační systémy lze pokládat za diskrétní, protože existuje tzv. kritérium věrnosti,[9] které udává rozklad množiny všech možných signálů na podmnožiny ekvivalentní z hlediska přijímače. U diskrétních systémů se věnuje pozornost sřetězovacím systémům (concatenation systems), jejich algebraické struktuře a vzájemným vztahům. Proud řeči se uvažuje jako posloupnost diskrétních prvků, které se kladou bezprostředně za sebe, tj. sřetězují se. Přirozený jazyk má podle Ch. a M. několik různých rovin, které lze chápat jako oddělené sřetězovací systémy obsahující vlastní prvky a pravidla. Struktura na nižší rovině je pak specifikována tím, jak se její prvky vztahují k rovině nejblíže vyšší (přístup celkem shodný s postupem v naší lingvistice).

Po uvedených obecných otázkách se přechází k výkladu o některých algebraických aspektech kódování, které se pokládá za zobrazení[9a] jednoho sřetězovacího systému do druhého. Kód je potom jednojednoznačné zobrazení řetězů slov ze slovníku V do řetězů znaků abecedy A, které je izomorfní vzhledem k operaci sřetězení. Ch. uvádí Schützenbergerovu klasifikaci kódů, která vychází z formálních vlastností kódů.

Dále se definují některé základní pojmy, např. jazyk. Jazyk L je množina vět (konečná nebo nekonečná), kde každá věta má konečnou délku a je vytvořena sřetězením konečné množiny prvků tvořících slovník V; do definice jazyka jsou zahrnuty jak jazyky přirozené, tak umělé — logické a programovací. Gramatika je pak množina pravidel, která rekurzívně specifikují věty jazyka a mají obecně tvar φ → ψ. Strukturním popisem se rozumí specifikování prvků, z nichž je věta vytvořena, specifikování jejich pořadí, vzájemného uspořádání, vztahů a jakékoli další informace potřebné k stanovení, jak se věta užívá a chápe v syntaktickém slova smyslu. Dále se vymezují pojmy jako frázový ukazatel, sebezapouštění, rekurzívní prvek, generativní a explikativní síla, které jsou čtenáři většinou známy.[10] Zajímavý je pojem stupeň gramatické správnosti, který je definován pro jazyk L generovaný generativní gramatikou G (dále GG). Množinu řetězů generovaných gramatikou G nečleníme na množinu L(G) řetězů gramaticky správných a množinu  řetězů gramaticky nesprávných, ale rozlišíme především podmnožinu L₁ vět gramaticky naprosto správných. Všechny ostatní řetězy generované gramatikou G uspořádáme podle stupně gramatické správnosti, který vyjadřuje skutečnost, že i řetězy, které nejsou v L₁, mohou mluvčí téhož jazyka pochopit dokonce nedvojznačně, protože je srovnávají s řetězy podmnožiny L₁.[11]

Následuje výklad o frázových GG (nověji složkově strukturních — constituent structure grammars), která se podrobněji probírají v pracích citovaných v pozn. 10. [74]Autoři pak přecházejí k problematice transformační gramatiky a nejprve objasňují nedostatky složkově strukturních gramatik. Ani tuto problematiku nebudeme tu probírat, hlavně proto, že dosavadní koncepce transformační gramatiky byla v poslední době podstatně přepracována.[12]

Poslední část kapitoly je věnována fonologické složce GG, jejíž úlohou je interpretovat koncové řetězy představující výstup ze syntaktické složky. Přesněji, tento výstup se skládá z lexikálních řetězů, jako John, book atd., a z gramatických řetězů, např. minulý čas, plurál aj. Fonologická složka obsahuje: 1. přepisovací pravidla včetně morfémově strukturních pravidel; 2. pravidla podobná pravidlům transformačním, která jsou uspořádána a aplikují se cyklicky; 3. přepisovací fonetická pravidla. Pravidla fonologické složky využívají syntaktické informace obsažené ve frázovém ukazateli. Ch. zaujímá kritický postoj ke klasické fonologii jako přechodné rovině mezi fonetickou a morfologickou rovinou v jazykovém systému a snaží se ukázat, že pro GG není taková rovina nutná, ale je nutná rovina morfonologická. Zároveň vyslovuje námitky proti některým tvrzením klasické fonologie (invariantnost, linearita).[13] Problematika fonologické složky GG je podrobně zpracována v nové práci Chomského a Halleho.[14]

4. V kapitole Formální vlastnosti gramatik probírá Ch. vztahy mezi frázovými gramatikami a abstraktními automaty, některé speciální třídy frázových gramatik a jejich formální vlastnosti. V souhlasu s předchozí kapitolou zavádějí se pojmy: generativní kapacita lingvistické teorie, tj. množina jazyků, které lze vytvořit gramatikami, jež tato teorie připouští, a explikativní kapacita, tj. množina systémů strukturních popisů, které lze vytvořit připuštěnými gramatikami. Chomského přehled je však z větší části omezen na generativní kapacitu frázových gramatik, protože jedině v této oblasti bylo dosaženo závažnějších výsledků. Studium explikativní kapacity empiricky platných teorií je však třeba pokládat za důležitější, protože bohatství a složitost dané teorie GG nelze měřit generativní kapacitou této teorie.

Dále se Ch. zabývá abstraktními automaty a jejich vztahy ke gramatikám a úvodem upozorňuje, že některé základní aspekty lingvistické teorie patří v zásadě k obecné teorii abstraktních automatů.[15] V této souvislosti se pokusíme seznámit čtenáře s některými základními pojmy teorie automatů.[16]

Nejjednodušším typem automatu je konečný automat, který je definován takto: F = ⟨A, S, f, S₀⟩, kde F je konečný automat, A = {a₀, a₁, …, a_D} je množina symbolů tvořících abecedu automatu F, přičemž symbol a₀ je identický prvek, S = {S₁, …, S_n} je množina vnitřních stavů automatu, f (a_i, S_j) = S_k je přechodová funkce, která pro symbol z abecedy A a daný vnitřní stav udává, do kterého dalšího stavu automat přejde, S₀ ∊ S je vyznačený počáteční a současně konečný stav automatu. Chování automatu F je popsáno konečnou množinou trojic (a_i, S_j, S_k), kde i, j, k jsou celá čísla splňující nerovnosti 0 ≦ i ≦ D a 1 ≦ j, k ≤ n. Trojici (a_i, S_j, S_k) lze interpretovat jako instrukci, která říká, že je-li automat F ve stavu S_j a čte vstupní symbol a_i, pak přejde do stavu S_k. Automat F při přecházení ze stavu do stavu přijímá (accepts) nebo generuje (generates) nějaký řetěz symbolů, který se nazývá věta [75]přijatá nebo generovaná automatem F. Řekneme, že řetěz x je věta přijatá (generovaná) konečným automatem F tehdy a jen tehdy, když existuje posloupnost symbolů (a_β1, …, a_βr) z abecedy automatu F a posloupnost vnitřních stavů S_γ1, …, S_{γr + 1} taková, že platí tyto čtyři podmínky: 1. první a poslední stav je vyznačený počáteční stav S₀; 2. všechny ostatní stavy se nerovnají počátečnímu stavu S₀; 3. (a_βi, S_γi, S_γi+1) je instrukce pro automat F pro každé i, kde i není nikdy větší než r; 4. pak x = a_β1 a_β2 … a_βr je řetěz symbolů přijatý (generovaný) automatem F.

Je naprosto nepodstatné, zda automat chápeme jako zdroj, který při přecházení z jednoho stavu do druhého generuje symboly, nebo jako zařízení přijímající vstupní symboly a přecházející přitom z jednoho stavu do druhého.

Konečný automat lze reprezentovat konečným orientovaným grafem s hranami označenými symboly abecedy A (viz obr. 1). Prostřednictvím tohoto grafu můžeme ukázat, jak automat F generuje (přijímá) konkrétní řetěz x = (a₁, a₄, a₇, a₉, a₀), tj. podle předchozího označování řetěz x = a_β1, a_β2, a_β3, a_β4, a_β5). Postup při generování (přijímání) této věty je dán instrukcemi: (a₁, S₀, S₁), (a₄, S₁, S₄), (a₇, S₄, S₅), (a₉, S₅, S₆), (a₀, S₆, S₀). Automat se nachází ve stavu S₀, čte vstupní symbol a₁ a přechází do stavu S₁. Nyní se nachází ve stavu S₁, čte symbol a₄ a přechází do stavu S₄. Podobně pokračuje dále uvedeným způsobem až nakonec se nachází ve stavu S₆, čte symbol a₀ a přechází do stavu S₀. Jak již víme, stav S₀ je počáteční (a konečný zároveň), tj. když se automat dostal do tohoto stavu, znamená to, že skončil, a tedy generoval (přijal) řetěz x = (a₁, a₄, a₇, a₉, a₀), který je větou jazyka generovaného automatem. Libovolná množina vět přijatá (generovaná) konečným automatem F se nazývá regulární jazyk (regulární jev).[17]

 

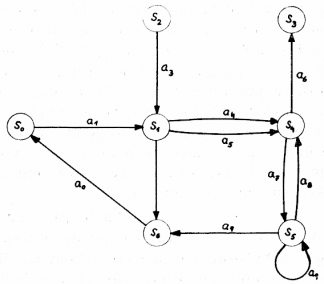
Obr. 1

 

Pozn.: Chování automatu z obr. 1 je definováno instrukcemi: (a₀, S₆, S₀), (a₁, S₀, S₁), (a₂, S₁, S₆), (a₃, S₂, S₁), (a₄, S₁, S₄), (a₅, S₁, S₄), (a₆, S₄, S₃), (a₇, S₄, S₅), (a₈, S₅, S₄), (a₉, S₅, S₅), (a₉, S₅, S₆). Čtenář si může podle uvedeného postupu samostatně ověřit, že automat F generuje rovněž např. větu y = a₁a₄a₇a₈a₇a₉a₀ nebo větu z = a₁a₅a₇a₉a₉a₉a₉a₀ aj.

V literatuře jsou abstraktní automaty obvykle interpretovány jako abstraktní zařízení skládající se z několika základních částí: 1. řadiče, který se může nacházet v konečném počtu stavů S = {S₀, …, S_n}; 2. čtecí hlavy, která je spojena s řadičem; 3. pásky, která je rozdělena na políčka a na níž se nacházejí nebo se na ni zapisují [76]symboly abecedy A = {a₀, a₁, …, a_D}. Páska je potenciálně nekonečná vpravo i vlevo a v případě konečného automatu se může pohybovat jen jedním směrem, např. zprava doleva tak, že když řadič přechází ze stavu S_j do stavu S_k a čtecí hlava čte symbol a_i, pak se páska posune o jedno políčko doleva. Uvažovat automaty jako zařízení obsahující tyto části není obecně nutné. Zdůrazňujeme, že existuje jen hrubá analogie mezi abstraktními automaty a samočinnými počítači. Automaty jsou matematické abstrakce, jichž se užívá při studiu některých druhů funkcí (rekurzívních) a jazyků v matematickém slova smyslu.

Dva automaty jsou ekvivalentní, generují-li stejné jazyky. V případě, že přechody z jednoho stavu do druhého jsou jednoznačně určeny, přesněji: 1. neexistuje-li možnost, že automat po generování symbolu a_i může přejít současně do dvou různých stavů S_k a S_m; 2. čte-li automat symbol a₀, pak musí vždy přejít do stavu S₀, ať se nachází v kterémkoli stavu. Splňuje-li konečný automat tyto podmínky, nazývá se deterministický.

Dalším typem konečného automatu je dvoucestný automat, který se od automatu F liší jinou definicí přechodové funkce, tj. f (a_i, S_j) = (S_k, l_h). Symbol l_h značí nový způsob posunu pásky, která se nyní může pohybovat v obou směrech, tj. nechť l_h = {l₁, l₂, l₃} kde l₁ vyjadřuje posun o jedno políčko vlevo, l₂ — páska se nepohybuje, l₃ — posun o jedno políčko vpravo. Chování tohoto automatu je popsáno konečnou množinou instrukcí (a_i, S_j, S_k, l_h), kde l_h je jedno z {l₁, l₂, l₃}.

Konečné automaty vymezují stejné jazyky jako konečně stavové gramatiky a bezkontextové (dále BK) jednostranně lineární gramatiky obsahující pouze pravidla buď tvaru A → xB, A → x, nebo A → Bx, A → x.

Silnějším typem automatu je lineárně ohraničený automat (dále LOA), který se od konečného automatu odlišuje tím, že má dvě abecedy, vstupní a výstupní, a jiný tvar přechodové funkce. Přesněji M = ⟨A_I, A_O, f, S, S_o⟩, kde A_I = {a_o, …, a_p} je vstupní abeceda, A_O = {a_o, …, a_p, …, a_q} je výstupní abeceda, je tedy vidět, že A_I ⊂ A_o, f je přechodová funkce f (a_i, S_j) = (S_k, l_h, a_m) vyjadřující, že automat při přechodu ze stavu S_j do stavu S_k přepisuje symbol a_i symbolem a_m. Chování automatu M je popsáno instrukcemi, které mají nyní tvar pětic (a_i, S_j, S_k, l_h, a_m). Generování řetězů je definováno stejně jako u konečného automatu, avšak pásky se nyní může užívat nejen jako vstupu, ale i jako paměti. Tyto dvě funkce lze od sebe oddělit a zavést u LOA dvě pásky, vstupní a paměťovou.

Jednou speciální třídou LOA se dvěma páskami jsou zásobníkové automaty (ZA). Vstupní páska ZA se může pohybovat jen jedním směrem a lze z ní pouze číst, paměťová páska se může pohybovat oběma směry: Pohybuje-li se vpravo, symboly se z ní čtou a pak vymazávají (nahrazují se symboly #), pohybuje-li se vlevo, symboly se na ni zapisují. Je tedy zřejmé, že v každém stavu je na paměťové pásce dostupný pouze nejpravější symbol, tj. ten, který byl zapsán poslední. Když se ZA dostane do stavu S_o, paměťová páska je prázdná, tj. obsahuje pouze symboly #. Nedeterministické ZA vymezují stejné jazyky jako BK gramatiky, proto se těchto automatů užívá při tzv. prediktivní analýze přirozených jazyků.[18] Modifikovaný ZA, jehož paměťová páska slouží jako výstupní a může se pohybovat jen jedním směrem — vlevo a který má tu vlastnost, že zobrazuje vstupní řetěz x do výstupního řetězu y, nazývá se konečný převodník a lze ho využít pro konstruování strukturních popisů vět přirozeného jazyka.

Nejvýše v hierarchii automatů stojí univerzální Turingovy automaty, které z LOA dostaneme tak, že k instrukcím pro LOA přidáme ještě instrukce tvaru (#, S_j, S_k, l_h, a_m), které říkají, že symbol # lze nyní přepsat jako symbol abecedy A. Automat může tedy užívat předtím nedostupné úseky pásky, která je zaplněna symboly [77]abecedy a symboly #. Chování Turingových automatů (dále TA) je podstatně jiné než chování předchozích typů automatů. TA může přijímat nějaký vstupní řetěz nekonečně dlouho, může přitom užít libovolně dlouhého úseku pásky, popř. pro daný vstupní řetěz se nemusíme vůbec dovědět, zda jej TA přijal nebo zda jej teprve přijme. Chování TA lze však nedvojznačně charakterizovat konečným počtem přepisovacích pravidel tvaru φ → ψ, kde φ, ψ jsou řetězy vytvořené z prvků konečného slovníku V. Konečná množina takových pravidel představuje vlastně nejobecnější možnou gramatiku, která se nazývá neomezený přepisovací systém (NPS). Gramatiky tohoto druhu jsou však pro svou vysokou nestrukturovanost lingvisticky málo zajímavé. Vztahy mezi jednotlivými typy gramatik a automatů lze vyjádřit přehledně graficky.[19] Vodorovné čáry označují, že daný typ automatu má stejnou generativní sílu jako daná gramatika. Pokud jde o transformační gramatiky, jejich vztah k automatům není zatím vyjasněn.

 

 

Obr. 2

 

Je však třeba upozornit, že těsné vztahy mezi generativními gramatikami a automaty naprosto neznamenají totožnost těchto pojmů. Tato zařízení jsou svou strukturou i způsobem činnosti různá, společné mají jen to, že mohou vymezovat stejné jazyky, tj. mohou být ekvivalentní co do generativní síly.

V dalším se probírají některé algebraické vlastnosti BKG, problematika strukturní víceznačnosti (ambiguity), která vzniká, když gramatika G generuje řetěz x dvěma různými způsoby, tj. přiřazuje mu dva odlišné strukturní popisy. Dále Ch. ukazuje, že jazyky je možno definovat soustavami rovnic, ale těchto výsledků nebylo zatím v lingvistice použito. Zmínka je věnována i programovacím jazykům, k jejichž popisu se dnes běžně užívá frázových gramatik.

V závěru Ch. upozorňuje, že všechny výzkumy v této oblasti mají předběžný charakter, protože se na této problematice pracuje teprve 5—6 let. Připomíná důrazně, že probírané systémy nejsou adekvátní pro postižení plné složitosti a bohatosti syn[78]taktických prostředků přirozených jazyků a že abstraktní studium tak bohatých a komplikovaných systémů a organismů, které jich užívají, vyžaduje jemnější nástroje a hlubší pohledy na formální systémy, než jsou dosavadní.

5. V kapitole Konečné modely uživatelů jazyka se zkoumá konstruování různých typů těchto modelů a jejich empirická adekvátnost. Při studiu modelů tohoto druhu musíme podle názorů M. a Ch. důsledně respektovat rozdíl mezi jazykovými znalostmi a schopnostmi mluvčího a jeho skutečným nebo potenciálním chováním, jinými slovy, je třeba rozlišovat formální popis nějakého jazyka (např. jeho GG) a model uživatele tohoto jazyka. M. a Ch. vycházejí z předpokladu, že teoreticky závažné aspekty „verbálního chování“ jsou společné pro mluvčího i posluchače a není mezi nimi zásadní rozdíl. Termín „uživatel jazyka“ (dále UJ) tedy zahrnuje mluvčího i posluchače.

První část kapitoly je věnována pravděpodobnostním modelům a mírám; jde tu zejména o Markovův zdroj, tj. nedeterministický konečný automat, který přechází ze stavu do stavu podle nějakého rozložení pravděpodobností. Modifikace Markovova zdroje, tj. k-omezený Markovův zdroj je pak zařízení, které může generovat aproximace skutečných textů na základě předem zjištěných četností výskytu symbolů.[20] Toto zařízení lze sice považovat za model UJ, má však zásadní nedostatek: nemůže nikdy izolovat množinu gramaticky správných vět, protože pro nepronesené gramaticky správné věty nelze odhadnout pravděpodobnosti. Kromě toho má model ještě další nedostatky.[21]

Další výklad se týká míry selektivní informace, redundance, kódů s minimální redundancí, tedy otázek vesměs dobře známých.[22] Zajímavý je pokus o stanovení míry gramatické správnosti vět, jejíž definice je podobná definici kapacity přenosového kanálu. Gramatika užívající této míry by nejen generovala věty s jejich strukturními popisy, ale každé větě by také přiřazovala stupeň gramatické správnosti vzhledem k množině gramaticky správných vět. Výklad o pravděpodobnostních modelech je uzavřen zkoumáním statistických aspektů slovníku, slovní zásoby a některých známých vztahů (Zipfův zákon).[23] M. a Ch. dospívají k jednoznačnému závěru: Stochastické modely a míry nejsou adekvátní pro popis UJ, protožo zachycují jen některé aspekty jeho „verbálního chování“. Chceme-li hlouběji pochopit strukturu přirozených jazyků a její užívání, musíme přejít k modelům, které lze nazvat algebraickými. Tento závěr by nebylo správné interpretovat jako odmítavý postoj k pravděpodobnostním modelům a teorii informace; spíše si M. a Ch. v plném rozsahu uvědomují nedostatečnost strukturního členění a malou generativní i explikativní sílu těchto postupů.

Algebraické modely UJ jsou aktivně rozpoznávací zařízení obsahující GG jako svou základní složku. M. a Ch. rozlišují modely obsahující frázové gramatiky (K nebo BK) a modely obsahující transformační G, o nichž se však nebudeme zmiňovat.[24] Probírají rovněž hypotézu Yngveho,[25] kterou přes četné výhrady v zásadě přijímají. Jako konkrétní příklad navrhují zařízení M, které by mohlo mít tyto části: 1. složku pro rozpoznávání řeči; 2. složku obsahující GG (BK), která analyzuje vstupní věty syntézou, tj. tak, že vstupní věty se porovnávají (match) se signály generovanými uvnitř M: [79]Nevznikl-li při porovnávání žádný rozpor, přechází se k dalšímu vstupu, vznikly-li nějaké neshody, zařízení M modifikuje svůj vnitřní signál tak dlouho, dokud výsledek porovnání není přijatelný nebo dokud vstup není zamítnut jako nesrozumitelný; 3. operační jednotku, která musí být schopna provádět různé logické operace. Přesněji, M = Ψ (G, m), kde Ψ je konečný převodník nedeterministický, G je bezkontextová gramatika generující vnitřní signály, m je počet sebezapouštění, který určuje, jaké nejsložitější věty může M přijímat. V závěru M. a Ch. činí některé předpoklady, které by mohly platit o M, ale ty se nakonec redukují na taková zřejmá tvrzení, jako že M je omezené konečné zařízení, které přiřazuje větám strukturní popisy, a že je omezeno lineárním průběhem času.

5.1 Psychologické názory M. a Ch. jsou nejkoncentrovaněji vyjádřeny v poslední části kapitoly o modelech UJ. Tato část obsahuje: 1. vyjmenování složek chování, 2. analýzu organizace chování. M. a Ch. uvádějí pět základních složek chování: 1. informaci a redundanci jako charakteristiky různosti nebo stereotypie posloupnosti chování; 2. stupeň sebezapouštění; 3. hloubku ve smyslu hypotézy Yngveho jako počet odsunutých symbolů v bezprostřední paměti (lze jí užít pro odhad schopnosti provádět složité instrukce); 4. strukturní složitost, tj. poměr celkového počtu uzlů k počtu uzlů koncových; 5. transformační složitost, tj. počet transformací potřebných pro změnu chování. Jednotlivé složky lze získat dvojím způsobem: Buď jde o psychologickou interpretaci gramatického jevu (v případě konstruování frázové a transformační složky chování), anebo se lingvistická hypotéza konstruuje na základě psychologických údajů (hypotéza Yngveho).

M. a Ch. chápou model uživatele jazyka jako zařízení (viz výše) obsahující generativní gramatiku s frázovou, popř. i s transformační složkou. Jednotkou konstrukce je jednotka analýzy chování, tj. systém TOTE, kde T, O, T, E jsou počáteční písmena označující funkce tohoto systému: test — operate — test — exit, tj. zkouška — činnost — zkouška — provedení. Svou koncepcí autoři navazují na učení psychologické školy nejvíce rozpracované v knize G. A. Millera, E. Galantera a K. H. Pribrama (o. c. v pozn. 21). V Millerově psychologii je výstavba intervenujících proměnných tvořena pojmovými konstrukty — plánem a obrazem. Neobehavioristické schéma S — O — R, kde R = f (S, O) je Millerem konkretizováno v „S — (obraz — plán) — R“, kde S = stimul, O = organismus, R = reakce.

Vznik pojmu TOTE souvisí s rozvojem psychoneurologie, která se zřetelně konstituovala v posledních pěti letech. Ukazuje se, že prosté reflexní schéma při výkladu jednotlivých forem chování nepostačuje. Psychologické teorie podmiňování mají dvojí představu o vzniku a průběhu reflexu: východiskem jedné bylo instrumentální podmiňování, tj. způsob podmiňování, při němž podmíněným podnětem je vlastní činnost živočicha hledajícího řešení úlohy (Lashley, Thorndike, Skinner), druhá představa byla součástí teorie klasického podmiňování (Pavlov). Systém TOTE jakožto jednotka analýzy chování individua překonává nedostatky dřívějšího pojetí jednotky chování, tj. prostého reflexního oblouku. TOTE zachovává principy instrumentálního podmiňování a obohacuje je o princip zpětné vazby. Skladbu TOTE lze schematicky znázornit, jak ukazuje obr. na s. 80.

Vznik reakce závisí na testování (vyhodnocení) působící energie. Reakce vzniká jen tehdy, je-li testování pozitivní. Testování se provádí podle určitých kritérii organismu. Pojem TOTE má funkce energetickou a regulační; lze jej postihnout i z hlediska teorie informace. Máme-li na mysli, že TOTE je schématem předávání energie, pak představuje reflex a jeho jednotlivé části odpovídají fyziologickým strukturám. Ve směru šipek probíhá i regulace. V tomto případě TOTE znázorňuje sled instrukcí, které zařízení musí provést, aby vyřešilo zadanou úlohu. Z hlediska teorie informace zaměřujeme pozornost na vstupní a výstupní stavy a zjišťování jejich vzájemné korelace.

[80]Systémy TOTE se organizují do složitých struktur, které mají mnoho shodného s frázovými ukazateli (viz výše), a to jak horizontálně, tak vertikálně. Pro každý typ chování existuje poněkud jiné uspořádání TOTE, tj. podle M. a Ch. plán, který je v podstatě programem pro počítač. TOTE je pak podplánem určitého plánu. Autoři uvádějí příklad organizace TOTE v podobě orientovaného grafu, který lze ztotožnit s konečným automatem (s. 74). I když uvádějí jen příklad plánu, je vidět, že systém TOTE je jednotkou analýzy jiných jednodušších i složitějších forem lidského chování.

 

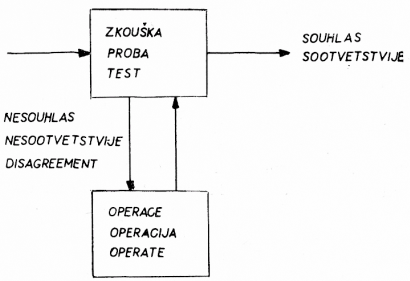
Obr. 3

 

5.2. Přednosti M. a Ch. koncepce modelu UJ vyvstanou, srovnáme-li ji s těmi pracemi, které se vztahují aspoň k jedné stránce užívání jazyka a jejichž teoretická východiska jsou obdobná. Jde tu především o Hockettův model posluchače a Osgoodův model porozumění a tvoření věty.[26] Hockett akceptuje pravděpodobnostní strukturu vztahů mezi jednotlivými gramatickými konstrukcemi; Osgood vychází z přizpůsobeného Markovova zdroje. Klady v pojetí M. a Ch. spočívají v tom, že se pravděpodobnostní podoba užívání jazyka začleňuje do strukturálních souvislostí, které jsou v mechanismech verbální produkce a percepce podstatné. Bez nich nelze vysvětlit, proč uživatel jazyka porozumí větě nové, a přitom je s to produkovat nové věty.

V chování člověka se uplatňují dva základní činitelé. Nazývají se různě: princip sukcesívní (postupný v čase) a simultánní (podněty přicházející z různých smyslů se současně skládají v jeden celek) syntézy, princip klasifikace a podmíněné probability, princip přiřazení a uspořádání v operačních teoriích intelektu apod. Vzhledem k těmto teoriím je skutečně odůvodněno přesvědčení, že Ch. učení ve své obecné podobě není jednostranné. Dosud neznáme mechanismy třebas jen ideálního uživatele jazyka. Ale v přístupu M. a Ch. spatřujeme řadu námětů pro konstruování experimentů, které by účast jednotlivých složek — pojmově oddělených — výrazně explikovaly. Velmi užitečné je srovnání s činností automatů (viz výše).

TOTE-jednotka rozvíjí teorii instrumentálního podmiňování, postrádáme však respektování fyziologie jednotlivých částí mozkového kmene, včetně výzkumů z oblasti retikulární formace, tj. nespecifické tkáni mozku, která má aktivační nebo tlumivou funkci v psychických činnostech. Obdobou TOTE-jednotky je Anochinovo učení o akceptoru činnosti a zpětné vazbě.[27] Postup M. a Ch. pokládáme za jeden z prvních [81]pokusů konstruovat psycholingvistickou jednotku verbální komunikace s přihlédnutím k psychologické realitě. Dřívější práce[28] vycházely z jednotek jazykového systému a připisovaly jim psychologickou funkci, aniž ověřily jejich vhodnost. Východiskem této koncepce je užívání jazyka, což zajišťuje adekvátní vystižení funkce psycholingvistické jednotky. Funkce těchto jednotek záleží podle našeho názoru v tom, že přiřazují strukturu myšlení struktuře jazyka v ontogenetickém i fylogenetickém řádu.

Kladně oceňujeme myšlenku autorů analyzovat složité formy chování pojmoslovím užitým k popisu UJ. V psychologii dosud nemáme inventář složitých forem chování, ani důkladný — strukturálnímu přístupu odpovídající — popis chování. Systém TOTE je explikátum,[29] které fixuje znaky vztahu společenského a individuálního, je však nutno prověřit vhodnost takové explikace. K výzkumu se nabízejí různé formy chování, v nichž je podstatný vzájemný vztah individuálního a společenského.

Psychologický přístup k jazyku lze jen vítat, i když je zatím jen programově nastíněn. Vědomí, a to jak společenské, tak individuální, je řízeno i psychologickými zákonitostmi. Protože jazyk je součástí společenského vědomí projevujícího se navenek, je nutné k těmto zákonitostem přihlížet. Obecně se tato potřeba formulovala často, ale málokdy se zdárně řešila. M. a Ch. koncepce je v tomto směru slibná.

6. Souhrnně můžeme říci, že recenzované tři kapitoly tvoří uzavřený celek a představují jednu etapu ve vývoji algebraické lingvistiky a jedné větve psycholingvistiky reprezentované především G. A. Millerem. Část výkladů o TG vychází ještě ze staršího pojetí, podle kterého se TG skládala ze dvou složek: syntaktické a fonologické. Nový vývoj koncepce TG a její přehodnocení nejsou ještě v těchto výkladech zachyceny.[30]

Stylem výkladu se jednotlivé kapitoly dosti liší. Kap. 11 „Úvod do formální analýzy přirozených jazyků“ je psána přístupně a předpokládá jen znalost některých základních pojmů teorie množin a moderní algebry. Naproti tomu kap. 12 „Formální vlastnosti gramatik“ je po matematické stránce dosti náročná a předpokládá částečnou předběžnou znalost teorie abstraktních automatů. Místy je však výklad téměř na hranici srozumitelnosti a některé formulace jsou nesystematické (výklad o převodnících a zásobníkových automatech, s. 346—352). Výklad v kap. 13 „Konečné modely uživatelů jazyka“ je opět srozumitelnější, i když se předpokládá znalost matematické statistiky, teorie pravděpodobnosti a teorie informace.

Práce Ch. a M. nejsou tedy právě lehkým čtením, ale jejich podrobné studium, které můžeme lingvistům jen doporučit, by rozptýlilo některé iluze o vztazích statistických a jiných modelů kódování a uživatelů jazyka. Ch. a M. se snaží rozšířit znalosti o jazykovém systému a jeho fungování z hlediska lingvistiky i psychologie, aniž podceňují složitost a obtížnost takového úkolu a aniž přeceňují své síly, což jim bývá někdy — neprávem — vytýkáno. S jejich některými názory a formulacemi by bylo možno nesouhlasit, ale takový rozbor by vyžadoval podstatně více místa. Lze jen litovat, že tyto práce jsou otištěny v publikaci málo dostupné širším vrstvám lingvistů.[31]

Karel Pala — Miluše Sedláková

Slovo a slovesnost, volume 27 (1966), number 1, pp. 71-81

Previous Kolektiv oddělení matematické lingvistiky ÚJČ: Sovětské sborníky o strukturní lingvistice

Next František Daneš: Dvě čítanky „pražské školy“