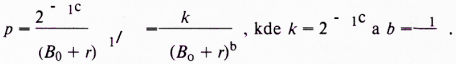Příspěvek k objektivizaci sémantických tříd
Martin Friš
[Articles]
A contribution to objectifying semantic classes
Pro zkoumání některých aspektů sémantiky přirozeného jazyka jsme zavedli sémantické třídy (Friš, 1983). Naše práce je motivována úsilím přispět k měření sémantické informace souvislého textu. Klasifikaci lexika do sémantických tříd pokládáme za jeden z možných výchozích bodů na této cestě. Možnost měřit sémantickou informaci ukazuje práce R. Carnapa a Bar Hillela (1954), která vychází z díla R. Carnapa (1950). Zmíněná práce poskytuje celkový rámec a základy pro zkoumání sémantické informace na rozdíl od statistického pojetí informace v práci C. Shannona (1948), založeného na pojetí entropie podle vzoru termodynamiky. Posouzení obou přístupů je možné nalézt u Brillouina (1964). Za východisko zavedených sémantických tříd byl vzat Rogetův tezaurus (1968). Protože jeho členění bylo příliš podrobné (obsahovalo 990 sémantických polí), byly z těchto skupin vytvořeny větší třídy. Principy tohoto třídění vycházejí z předpokladu, že klasifikace slovní zásoby předpokládá implicitně či explicitně i jisté filozofické východisko, jistý pohled na realitu.
Vedle seskupení slov do větších tříd (celkem 32) jsme provedli i jisté přeřazení a změnu pořadí v skupinách Rogetových. Klasifikace má vycházet i z jistých přesných kritérií (Voronin, 1985) a umožňovat jistou měřitelnost. Pak nejjednodušší číselné měřítko je prosté lineární uspořádání měřené pořadovými čísly (ordinály), zde čísly přirozenými. Přitom obvykle v případech, kdy se ještě nemůžeme propracovat k exaktnějším číselným měřítkům, uplatňuje se zásada, že první třídy jsou nejelementárnější a že na konci škály přicházíme k jevům nejkomplexnějším. Přihlížíme zároveň k důležitosti jevů v tom smyslu, co je předpokladem čeho, že elementárnější je předpokladem komplexnějšího. Do určité míry je to vlastně atomické pojetí světa, jevů. V našem případě směr uspořádání od elementárního ke komplexnímu obvykle odpovídá genetické a vývojové linii světa.
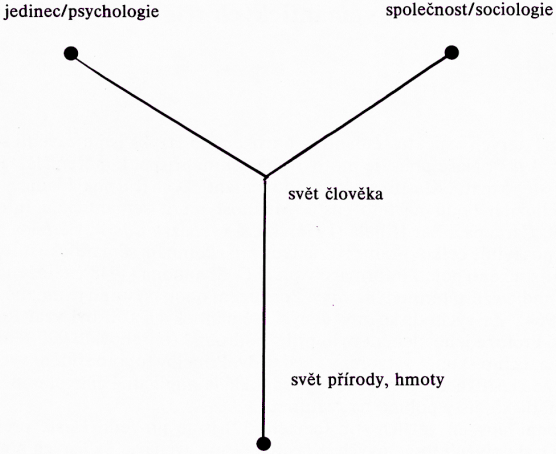
Krátce vyznačíme rozdíl mezi lineárním uspořádáním Rogetovým a přeuspořádáním naším. Oproti Rogetovi řadíme pojmy o hmotě před pojmy o člověku, vzhledem k evoluční následnosti. Obtížnější je řešení pořadí globálních skupin pojmů společnosti (sociologie) x jedince (psychologie). Na tento problém existují samozřejmě různé pohledy. Tato problematika souvisí s problematikou klasifikace věd, pro podrobnější diskusi odkazuji na knihu E. D. Graždanikova (1987). V tomto článku se kloníme k pojetí, že nejvýstižnější řešení je zde porušit striktní linearitu, která určuje, co předchází a co následuje, a říci, že svět přírody předchází jak člověka, tak společnost, ale postavit jak pojmy o společnosti, tak o člověku na stejnou úroveň. Na této úrovni je pak vzájemné působení. Tím tedy místo prosté linearity dostaneme rozvětvení, tedy jen částečné uspořádání v striktním matematickém smyslu (např. Beran, 1972). Schematicky na obrázku:
[24]
Rogetovo pojetí jsme obohatili o jistý přístup k výběru slov. Ačkoliv počet slov zpracovaný Rogetem je značný – asi 10 000, přesto některá běžná slova chybějí. Roget neměl v úmyslu zpracovat co největší rozsah slovní zásoby, ale vypracovat pomůcku, které by bylo možno využít k lepší stylizaci, výběru jazykových prostředků spisovatelů, novinářů, uživatelů jazyka vůbec. Rovněž tak je tomu se slovníky (Hallig – Wartburg, 1963; Český slovník věcný a synonymický, 1969–1977).
Výběr slov z celkové slovní zásoby jsme řešili tak, že jsme se rozhodli vybrat jen slova nejdůležitější, a to podle jistého kritéria. Na současné úrovni lingvistického poznání považujeme za nejvhodnější a zároveň měřitelný stupeň důležitosti frekvenci slova v reprezentativním frekvenčním slovníku (srov. Quine, 1969). Za reprezentativní frekvenční slovník pro češtinu jsme zvolili slovník Jelínek – Bečka – Těšitelová (1961), který pro obecnou slovní zásobu je dosud jediným takovým publikovaným dílem pro češtinu. Vybrali jsme nejprve všechna slova nejfrekventovanější do pořadí 2000, potom i do pořadí 3500. Základní obraz výsledků se tím nijak nezměnil. Další rozšiřování počtu zpracovávaných slov čistě mechanicky na slova se stále nižším pořadím (rankem), a tím i nižší frekvencí vede k zajímavým problémům. Zde jen poznamenáme, že prosté mechanické rozšiřování výběru ze slovní zásoby postupně ztrácí svou účinnost, a je tedy třeba hledat metody nové a účinnější. Rovněž je třeba poznamenat, že použití frekvenčního principu vede k výsledkům relativním, ne absolutním. Relativní tu neznamená libovolný, ale vztažený k nějakému referenčnímu rámci. Pokud použijeme jiný frekvenční slovník, sestavený na základě jiného výběru textů z množství publikovaných textů, dostaneme jiný frekvenční seznam, a tedy i kritérium výběru bude dávat poněkud odlišné konkrétní výsledky. V češtině byly dále sestaveny frekvenční slovníky z textů vědeckých, a to technických a přírodních (Bečka, 1974), a z textů věcného stylu, publicistického, odborného a administrativního (Těšitelová et al., 1983). Nicméně porovnání frekvenčního seznamu prvních dvou tisíc slov ve slovnících pro češtinu (Jelínek – Bečka – Těšitelová, 1961), angličtinu (Thorndike – Lorge, 1972), ruštinu (Šteinfeldt, 1963), němčinu (Rachmanov, 1967) ukazuje, že v těchto seznamech jsou velké shody.
Náš výzkum slovní zásoby vychází ze spojení dvou principů:
| primárního | – metoda sémantických polí, |
| sekundárního | – metoda frekvenční. |
[25]Podobný přístup zpracování, jako je náš, je použit i v knize V. V. Morkovkina et al. (1984), kde jsou slova rozčleněna do 29 tříd a 254 skupin podle kombinovaných údajů 8 frekvenčních slovníků ruského jazyka. Na tento slovník pak navazuje další práce V. V. Morkovkina et al. (1985).
Účelem tohoto článku je zkoumat objektivní platnost sémantických polí a přispět k objektivně platné klasifikaci slov z hlediska sémantiky porovnáním různých sémantických systémů a klasifikačních schémat. Ačkoliv výzkum sémantických polí se v lingvistice uplatňuje již dávno, jsou proti němu vznášeny zejména námitky, že výběr sémantických polí je údajně závislý jen na subjektivitě autora. Proti tomu můžeme namítat:
(1) Existuje vzájemná převoditelnost (tj. přeložitelnost) jednoho systému sémantických polí na systémy jiné. Provedli jsme převod své klasifikace na klasifikaci tezauru Rogetova a na klasifikaci Českého slovníku věcného a synonymického.
(2) Rozdělení sémantických tříd v souvislém standardním beletristickém textu je statisticky vzato homogenní. Zjistili jsme to konkrétně na materiálu knihy V. Řezáče, Rozhraní. Příklad nehomogenity rozdělení sémantických tříd jsme našli v souvislém vědeckém textu, konkrétně Sedláček, 1981.
(3) Klasifikaci slovní zásoby pomocí sémantických tříd jsme porovnali a uvedli do souvislosti s klasifikací vědních oborů (založenou na seznamu vysokých škol).
(4) Pro slova v těchto sémantických třídách (jako podmnožiny celých textů) platí Zipfův zákon (srov. odd. 4).
Cesta k objektivizaci zřejmě vede přes intersubjektivní fázi, tj. střetnutí více subjektivních východisek a jejich následné vyrovnání do jakési sjednocující koncepce. Cesta přes intersubjektivní fázi je přirozená a asi ji nelze obejít při řešení protikladu subjektivní – objektivní.
1. Vytvoření sémantických polí
Pro vytvoření struktury sémantických polí využijeme vztah sémantické blízkosti či podobnosti slov. Tento vztah je vlastně rozšířením klasického vztahu dvou slov, mezi nimiž platí synonymie. Pro zpřesnění si vybereme jeden rys, který exaktně vymezíme. Z důvodů terminologických zvolíme termín srovnatelný (významem). O dvou slovech a, b řekneme, že jsou srovnatelná či nesrovnatelná významem. Relaci srovnatelnosti budeme značit COM. Pak tedy platí buď COM (a,b), nebo neplatí COM (a,b,). Jde o binární relaci, jíž množinu slov rozdělíme na třídy ekvivalence, a to zcela konstruktivně tím, že předložíme seznam všech slov v jednotlivých třídách. Podle klasické partie teorie množin (např. Kuratowski – Mostowski, 1968), jak známo, mají třídy ekvivalence tyto vlastnosti:
1) každý prvek patří právě do jedné třídy,
2) třídy jsou párově disjunktní,
3) jejich sjednocení dává celou množinu.
Koncepce opřená o relaci srovnatelnosti nám dává možnost mluvit o sémantických třídách, nikoli jen o sémantických polích. V rámci této práce pokládáme oba termíny za ekvivalentní a oba budeme používat ve vhodných kontextech. Termín sémantická třída má oporu v terminologii matematiky a matematické logiky.
2. Určení podobnosti slov
Mluvčí jazyka je zpravidla schopen odpovědět na otázku, jsou-li si dvě slova podobná, nebo ne, tj. srovnatelná významem. Můžeme se mluvčího např. dotazovat, proč danou dvojici slov považuje za podobnou, či ne, můžeme dokonce měřit nějaké jeho psychologicko–fyziologické reakce (takové pokusy se dělaly, viz Fiala, 1982). Když bude mluvčí vysvětlovat, proč považuje nějakou dvojici slov za srovnatelnou, či nikoli, [26]bude jistě odkazovat na význam slova, na jeho výklad. Avšak výkladové slovníky jsou z principu neuspokojivé. Pokoušíme se řešit problém vymezení významu slova tím, že ho zařazujeme do vyššího významového rámce, kterým je pro nás konkrétní obor vědy. Pro tento účel jsme stanovili korespondenci mezi sémantickými třídami a konkrétními vědeckými obory.
3. Vlastnosti soustav sémantických polí
Podle našeho názoru je pro soustavu sémantických polí výhodné, aby se vyznačovala těmito vlastnostmi:
1) Obsahovala malý počet základních polí – a to pro přehlednost.
2) Obsáhlejší třídy by měly být rozčleněny na stejný počet tříd nižšího stupně.
3) Měla by obsahovat všechna slova vymezená jistým přesným kritériem, tj. měla by být univerzální.
Ad 1): V uvedeném systému sémantických tříd rozlišuji 32 tříd. Při práci s počítačem lze pak postupovat tak, že sestavíme slovník daného textu. Ke každému slovu slovníku přiřadíme jeho překlad do sémantické třídy, tj. zařazení do jedné ze sémantických tříd, a slovo označíme číslem té třídy, do které patří. Pak program čte text, vyhledá pro každé další slovo jeho překlad do sémantické třídy a zapíše ho jako příslušné číslo 1 až 32. Odpovídající počítačový program byl již implementován na PC a bylo jím reálně zpracováno přes 90 stránek souvislého textu z těchto knih: V. Řezáč, Rozhraní; J. Sedláček, Úvod do teorie grafů; L. Beran, Grupy a svazy. V tomto pojetí (překlad českého textu do sémantických tříd) lze pak toto značení chápat jako jednoduchý jazyk, který se skládá jen ze znaků 1–32. Nazveme jej jazyk ORBIS.
Ad 2): Každá sémantická třída se člení na tři podtřídy, nazývané sémantické skupiny, tak, že do skupin byla zařazena slova, která si jsou významem nejbližší. Rozdělení na tři skupiny bylo provedeno jako záměrná konstrukce. Z praktických důvodů byla dána přednost tomuto rozdělení před rozdělením na 2, 4 či 5 skupin. Toto rozdělení na skupiny též splňuje dvě vlastnosti: (1) počet slov ve skupinách je zhruba stejný, tj. obsahuje-li nějaká třída např. 60 slov, pak skupiny 1., 2. a 3. obsahují zhruba po 20 slovech. (2) Je možné pozorovat tendenci, že v seznamu slov libovolné třídy uspořádaném podle klesající frekvence je zastoupení slov podle příslušnosti do skupin zhruba rovnoměrné.
Ad 3): Slovník zařazující slova do sémantických tříd zahrnuje všechna slova do jisté úrovně podle přesně vyjádřitelného kritéria frekvence. Běžné slovníky sémantických polí některá slova základní i velmi frekventovaná neuvádějí. V tezauru Rogetově nenajdeme např. slovo bridge (most). V Českém slovníku věcném a synonymickém nenajdeme např. předložky. Autoři těchto slovníků vidí jejich hlavní určení v použití pro stylistické účely. Je-li však třídění univerzální, pak umožňuje zpracovat souvislý text a překlad do jazyka sémantických tříd (např. ORBIS).
4. Sémantické třídy a první Zipfův zákon
Zipf (1949) na rozsáhlém materiálu vyjádřil statistickou zákonitost mezi frekvencí f a rankem r ve frekvenčním seznamu uspořádaném podle klesající frekvence slov:
r ∙ f = k (konstanta).
Tato Zipfova zákonitost má širší oblast použití, nevztahuje se pouze na jevy jazykové, ale i na jevy v ekonomické geografii. Platí např. pro vztah mezi pořadím města podle jeho velikosti (počtu jeho obyvatel) a počtem jeho obyvatel.
Později se zabýval poměrem mezi rankem a frekvencí Mandelbrot (1954). Platnost vztahu mezi pořadím slov a frekvencí se totiž výrazně porušuje pro počáteční úsek slov frekvenčního seznamu a též pro koncový úsek je shoda slabší. Mandelbrot zavedl zobecňující modifikaci, zvanou kanonický zákon, kde se vyskytují další dvě konstanty Bo, b.
f = k/ (Bo + r)b.
[27]Tím se také vhodnou volbou konstant Bo, b lépe vystihují různé typy textů. Mandelbrot dále podal za jistých zjednodušujících předpokladů matematický důkaz svého kanonického zákona jako řešení optimalizační úlohy z teorie informací. Přístupný výklad je podán u Brillouina (1964) nebo detailně v diplomové práci V. Valoucha (1969). Hlavní myšlenky důkazu zde uvedeme ve zkratce.
1) Určíme počet textů N(t), které při daném kódování mají celkovou cenu t.
2) Dále vyřešíme úlohu, jak maximalizovat pro text, jehož celková cena je t, jeho celkovou informaci
i = – N ∙ ∑ pj log pj
tj. určit, pro jaká pj a N je hodnota funkce i maximální.
3) Dalším odvozováním dostaneme nakonec:
Odtud po úpravách závěrečné:
Naproti tomu ostré polemické výhrady k Zipfovu prvnímu zákonu byly publikovány Herdanem (1962, 1964). Zajímavou interpretaci zákona na základě Paretovy distribuce podává Králík (1988).
Jako východisko našich úvah zde vezmeme empirické pozorování, že jistým „rozmazaným” způsobem je Zipfova zákonitost splněna pro frekvenční seznam slovníku Jelínek – Bečka – Těšitelová (1961). Konkrétně pro slova v rozmezí pořadí mezi 2000 a 10 000 je konstanta k = r ∙ f v průměru rovna 165 000, hranice horní odchylky je 194 000 a hranice dolní odchylky je 140 000, srov.:
| r | f | r ∙ f = k |
| 2000 | 97 | 194 000 |
| 3000 | 62 | 186 000 |
| 4000 | 44 | 176 000 |
| 5000 | 33 | 165 000 |
| 6000 | 27 | 162 000 |
| 7000 | 22 | 154 000 |
| 8000 | 18 | 144 000 |
| 9000 | 16 | 144 000 |
| 10000 | 14 | 140 000 |
Prozkoumejme, jak se zachová platnost zákonitosti při jistých regulárních výběrech slov z celkového frekvenčního seznamu. Předpokládejme, že na nějakém dostatečně rozsáhlém slovním materiálu je poměr mezi pořadím a frekvencí slova zcela ideálně splněn, tj. f ∙ r = k (konst.). Předpokládejme, že k je velké, např. k = 10 000. Ze vzorce pak plyne, že 10. slovo má frekvenci 1000, 20. slovo frekvenci 10 000/20 = 500, 30. slovo 10 000/30 = 333, 40. slovo frekvenci 250. Ze seznamu slov udělejme dále výběr tak, že vezmeme pouze 10. slovo, 20. slovo, 30., 40., tj. každé desáté. Tento výběr nazveme regulární. Slova tohoto výběru mají frekvence postupně: 1000, 500, 333, 250, 200, 166 atd., a tedy také splňují Zipfův první zákon, a to s konstantou 10krát menší, než byla původní k = 10 000.
[28]Formální důkaz je snadný. Je-li f ∙ r = k, pak f ∙ r/10 = k/10. Pro r/10 zavedeme novou proměnnou r’. Pak platí f ∙ r’ = k/10 = k’. Připomínáme, že r’ označuje pořadí v provedeném regulárním výběru. Je tedy vidět, že pro něj platí Zipfův zákon, ale s konstantou k’.
Jestliže tedy náš výběr slov z frekvenčního seznamu 2000 nejfrekventovanějších slov (podle slovníku Jelínek – Bečka – Těšitelová, 1961) vzniklý rozdělením do sémantických tříd bude regulární (s jistými dostatečně malými odchylkami), pak i slova v sémantických třídách uspořádaná podle frekvence budou splňovat Zipfův první zákon. O tom jsme se přesvědčili propočítáním všech příslušných r’ ∙ f. Souhrnný výsledek s uvedením statistické standardní odchylky je uveden v tabulce č. 2, a jak se zákonitost projevuje pro jednu konkrétní třídu, je uvedeno v tabulce č. 3.
Pro větší názornost uvádíme i následující aproximaci. Stačí si uvědomit, že regulární výběr má i tu vlastnost, že rozdělíme-li seznam slov na čtyři skupiny podle pořadí takto:
A: pořadí 1–500, B: pořadí 501–1000, C: pořadí 1001–1500, D: pořadí 1501–2000, pak počet slov regulárního výběru v intervalech A, B, C, D musí být v ideálním případě stejný. Tj. je-li např. počet slov v regulárním výběru 52, pak v intervalech A, B, C, D by mělo být po 52/4=13. Tuto vlastnost můžeme empiricky pozorovat v tabulce č. 1, kde jsou zároveň vidět reálné odchylky od ideálního vzoru.
Shrnujeme: Pro zde uváděnou klasifikaci sémantických tříd platí v jistých dostatečných mezích Zipfův první zákon.
Získané výsledky jsou jen prvními kroky na cestě zkoumání této oblasti a nemusí se jevit jako zcela přesvědčivé. Pokud však tento článek podnítí další výzkum v této oblasti, bude tím jeho poslání naplněno. Jako nejúčelnější se nyní jeví prozkoumat jeden rozsáhlý souvislý text z beletrie.
5. Závěr
Ve své práci jsme představili jazyk sémantických tříd ORBIS a uvedli některé jeho vlastnosti. Jiný jazyk sémantických tříd v češtině je jazyk SEMAN, vypracovaný v pražském Ústředí vědeckých, technických a ekonomických informací (ÚVTEI) a aplikovaný na zpracovávání rešerší. Krátce se zmíníme o srovnání jazyků SEMAN a ORBIS. Nejedná se o dva jazyky konkurenční, ale komplementární. Hlavní kontrastní rys je, že jazyk SEMAN je analytický, zatímco ORBIS je syntetický. SEMAN jednomu slovu přiřazuje více znaků na základě výkladové definice slova, naproti tomu ORBIS více slovům přiřazuje jediný společný znak.
Metoda sémantické klasifikace jazyka se ve spojení s počítačem řadí mezi současné proudy zpracování textů počítačem.
|
| sémantická třída | celkem | A | B | C | D | |
| 01 | bytí, událost | 28 | 08 | 10 | 06 | 04 | |
| 02 | vztah, seskupení | 49 | 16 | 14 | 11 | 08 | |
| 03 | množství, číslo | 52 | 14 | 17 | 08 | 13 | |
| 04 | řád, zákonitost | 51 | 13 | 12 | 13 | 13 | |
| 05 | změna, příčina | 70 | 12 | 24 | 22 | 12 | |
| 06 | čas, období | 34 | 12 | 12 | 04 | 06 | |
| 07 | průběh času | 52 | 18 | 14 | 12 | 08 | |
| 08 | prostor | 50 | 10 | 12 | 13 | 15 | |
| 09 | tvar | 37 | 05 | 10 | 13 | 09 | |
| 10 | pohyb | 62 | 13 | 09 | 15 | 25 | |
| 11 | přenos, změna polohy | 43 | 04 | 12 | 12 | 15 | |
| 12 | hmota, krajina | 45 | 08 | 12 | 11 | 14 | |
| 13 | vlastnosti hmoty, smysly | 77 | 15 | 20 | 23 | 19 | |
| [29] | sémantická třída | celkem | A | B | C | D | |
| 14 | živočich, biologická činnost | 42 | 11 | 08 | 13 | 10 | |
| 15 | části organismu | 43 | 09 | 12 | 13 | 09 | |
| 16 | práce, činnost | 42 | 17 | 02 | 08 | 15 | |
| 17 | zemědělství, průmysl, doprava | 49 | 06 | 17 | 09 | 17 | |
| 18 | obchod, majetek, dát | 61 | 15 | 16 | 15 | 15 | |
| 19 | úřad, řízení, výchova | 61 | 03 | 13 | 25 | 20 | |
| 20 | společnost, stát, skupina | 62 | 16 | 17 | 17 | 13 | |
| 21 | boj, politika, armáda | 40 | 03 | 12 | 05 | 20 | |
| 22 | vztahy mezi lidmi, morálka | 63 | 08 | 17 | 15 | 23 | |
| 23 | rodina, sex, přátelství | 69 | 18 | 18 | 16 | 17 | |
| 24 | město, obydlí, domácnost | 47 | 10 | 13 | 12 | 12 | |
| 25 | oděv, jídlo, nemoc | 30 | 02 | 11 | 06 | 11 | |
| 26 | zpráva, řeč, psaní | 53 | 11 | 18 | 13 | 11 | |
| 27 | hledání, vyučování, pravda | 71 | 16 | 11 | 25 | 19 | |
| 28 | myšlení, vědomost | 69 | 11 | 23 | 19 | 16 | |
| 29 | věda, umění, náboženství | 47 | 06 | 16 | 16 | 09 | |
| 30 | charakter, zážitek, zábava | 48 | 09 | 14 | 13 | 12 | |
| 31 | nálada, dojmy, city | 49 | 07 | 17 | 13 | 12 | |
| 32 | lidská situace | 39 | 02 | 05 | 11 | 21 | |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
| suma celkem | 1635 |
|
|
|
|
|
|
| slova gramatická a jména | 365 |
|
|
|
|
A, B, C, D označují klesající pořadí v seznamu prvních 2000 slov uspořádaných podle frekvence (podle údajů frekvenčního slovníku Jelínek – Bečka – Těšitelová)
A označuje slova v pořadí 1–500,
B označuje slova v pořadí 501–1000,
C označuje slova v pořadí 1001–1500,
D označuje slova v pořadí 1501–2000.
Pod záhlavím celkem je uveden celkový počet slov v dané sémantické třídě. Pod záhlavím A, B, C, D je uveden počet slov, která se vyskytují v příslušném intervalu pořadí.
Tab. č. 2: Zipfova zákonitost pro sémantické třídy a meze její platnosti
| 1. |
| 2. |
| 3. |
|
| 03 |
| 5718 |
| 1097 |
|
| 04 |
| 5050 |
| 982 |
|
| 05 |
| 6982 |
| 1156 |
|
| 06 |
| 4761 |
| 1125 |
|
| 07 |
| 6704 |
| 1286 |
|
| 08 |
| 4461 |
| 886 |
|
| 09 |
| 3304 |
| 757 |
|
| 10 |
| 5043 |
| 929 |
|
| 11 |
| 3659 |
| 777 |
|
| 12 |
| 4120 |
| 854 |
|
| 13 |
| 6559 |
| 1293 |
|
| 14 |
| 4298 |
| 917 |
|
| 15 |
| 4465 |
| 945 |
|
| 16 |
| 4579 |
| 977 |
|
| 17 |
| 4104 |
| 816 |
|
| 18 |
| 5929 |
| 1055 |
|
| [30]1. |
| 2. |
| 3. |
|
| 19 |
| 4729 |
| 846 |
|
| 20 |
| 6399 |
| 1130 |
|
| 21 |
| 3005 |
| 671 |
|
| 22 |
| 4989 |
| 877 |
|
| 23 |
| 6892 |
| 1154 |
|
| 24 |
| 4485 |
| 910 |
|
| 25 |
| 2710 |
| 689 |
|
| 26 |
| 5316 |
| 1015 |
|
| 27 |
| 6261 |
| 1035 |
|
| 28 |
| 5765 |
| 1137 |
|
| 29 |
| 4459 |
| 906 |
|
| 30 |
| 4568 |
| 916 |
|
| 31 |
| 4326 |
| 871 |
|
| 32 |
| 2643 |
| 600 |
|
Legenda:
Sloupec č. 1 označuje číslo sémantické třídy – tak, jak jsou očíslovány v tab. č. 1.
Sloupec č. 2 uvádí aritmetický průměr součinů r ∙ f, tj. pořadí krát frekvence. Do výpočtu není zařazeno prvních pět slov v pořadí, kde – jak známo – jsou odchylky od Zipfova zákona největší.
Sloupec č. 3 uvádí standardní odchylku od aritmetického průměru.
Ve dvou případech – třídy 13, 28 – byl výpočet aritmetického průměru a standardní odchylky z technických důvodů proveden jen pro prvních 50 slov.
Konkrétní představu, jaké jsou velikosti frekvence a součinu pořadí a frekvence a jejich odchylky od vypočteného aritmetického průměru, je možné získat z tab. č. 3, kde jsou uvedeny tyto hodnoty pro sémantickou třídu 4.
| r |
| frekv. | r ∙ frekv. | ||||
| 01 | poslední | 902 | 902 | ||||
| 02 | opět | 683 | 1366 | ||||
| 03 | stejně | 630 | 1890 | ||||
| 04 | hlavní | 604 | 2416 | ||||
| 05 | třída | 555 | 2775 | ||||
| 06 | určitý | 533 | 3198 | ||||
| 07 | řada | 531 | 3717 | ||||
| 08 | zvláštní | 510 | 4080 | ||||
| 09 | stupeň | 504 | 4536 | ||||
| 10 | způsob | 500 | 5000 | ||||
| 11 | základ | 486 | 5346 | ||||
| 12 | metoda | 416 | 4992 | ||||
| 13 | druh (neživ.) | 385 | 5005 | ||||
| 14 | základní | 366 | 5124 | ||||
| 15 | funkce | 327 | 4905 | ||||
| 16 | obor | 309 | 4944 | ||||
| 17 | řád | 294 | 4998 | ||||
| 18 | pořádek | 283 | 5094 | ||||
| 19 | obecný | 262 | 4978 | ||||
| 20 | typ | 234 | 4680 | ||||
| 21 | prostý | 232 | 4872 | ||||
| 22 | systém | 227 | 4994 | ||||
| 23 | soustava | 212 | 4876 | ||||
| [31]r |
| frekv. | r ∙ frekv. | ||||
| 24 | obyčejný | 209 | 5016 | ||||
| 25 | úplně | 204 | 5100 | ||||
| 26 | normální | 196 | 5096 | ||||
| 27 | rytmus | 180 | 4860 | ||||
| 28 | jednoduchý | 179 | 5012 | ||||
| 29 | přirozený | 169 | 4901 | ||||
| 30 | průměrný | 160 | 4800 | ||||
| 31 | struktura | 159 | 4929 | ||||
| 32 | náhoda | 151 | 4832 | ||||
| 33 | zvyk | 148 | 4884 | ||||
| 34 | ráz (subst.) | 148 | 5032 | ||||
| 35 | zařízení | 148 | 5180 | ||||
| 36 | podivný | 145 | 5220 | ||||
| 37 | složitý | 140 | 5180 | ||||
| 38 | úroveň | 140 | 5320 | ||||
| 39 | obyčejně | 127 | 4953 | ||||
| 40 | souvislost | 124 | 4960 | ||||
| 41 | všeobecný | 121 | 4961 | ||||
| 42 | odvětví | 120 | 5040 | ||||
| 43 | pravděpodobnost | 118 | 5074 | ||||
| 44 | náhodný | 117 | 5148 | ||||
| 45 | zpravidla | 116 | 5220 | ||||
| 46 | samostatný | 115 | 5290 | ||||
| 47 | zmatek | 112 | 5264 | ||||
| 48 | určitě | 108 | 5184 | ||||
| 49 | řádný | 105 | 5145 | ||||
| 50 | příslušný | 104 | 5200 | ||||
| 51 | princip | 100 | 5100 | ||||
|
| s výjimkou prvních pěti slov: |
| |||||
|
|
| maximum: 5346 | minimum: | 3198 | |||
|
|
| průměr: 5050 | standardní odchylka: | 982 | |||
LITERATURA
Bečka, J. V.: Lexikální složení českých odborných textů technického zaměření. Praha 1974.
Beran, L.: Grupy a svazy. Praha 1974.
Brillouin, L.: Nauka i teorija informacij. Moskva 1964.
Carnap, R.: Logical Foundations of Inductive Probability. Chicago 1950.
Carnap, R. – Bar–Hillel, Y.: Sémantická informace. In: Teorie informace a jazykověda. Praha 1964, s. 165–175.
Český slovník věcný a synonymický. Haller J. et al. 3. vyd. Praha 1977.
Fiala, J.: Labyrinty jazyka. Praha 1982.
Friš, M.: The frequency and ideographic classification in a thesaurus. Prague Bulletin of Mathematical Linguistics, 41, 1983, s. 36–46.
Graždanikov, E. D.: Metod postrojenija sistemnoj klassifikacii nauk. Novosibirsk 1987.
Hallig, R. – Wartburg, W.: Begriffsystem als Grundlage für die Lexikographie. Berlin 1963.
Herdan, G.: The Calculus of Linguistic Observations. Haag 1962.
Herdan, G.: Quantitative Linguistics. London 1964.
Jelínek, J. – Bečka, J. V. – Těšitelová, M.: Frekvence slov, slovních druhů a tvarů v českém jazyce. Praha 1961.
[32]Komenský, J. A.: Orbis pictus. Praha 1941.
Kosovskij, B. I.: Obščeje jazykoznanije. Minsk 1974.
Králík, J.: Some notes on the frequency–rank relation. Prague Studies in Mathematical Linguistics, 8, 1983, s. 67–80.
Kuratowski, K. – Mostowski, A.: Set Theory. Amsterdam 1968.
Longman Lexicon of Contemporary English. McArthur T. London 1985.
Morkovkin, V. V. et al.: Leksičeskaja osnova russkogo jazyka. Moskva 1984.
Morkovkin, V. V. et al.: Leksičeskoje minimum sovremennogo russkogo jazyka. Moskva 1985.
Quine, W. O.: The Ways of Paradox. Cambridge, Mass. 1969.
Rachmanov, I. V.: Slovar’ naiboleje upotrebitel’nych slov nemeckogo jazyka. Moskva 1967.
Roget Thesaurus. Penguin books, Hardmondsworth 1968.
Sedláček, J. Úvod do teorie grafů. Praha 1981.
Shannon, C. E.: A mathematical theory of communication. Bell Syst. Tech. Journal, 27, 1948, s. 379–423, 623–656.
Smetáček, V.: Sémantický analyzátor. Úvod do problematiky. Olomouc 1982.
Smetáček, V.: Sémantický analyzátor. Experimentální ověřování. Olomouc 1984.
Smetáček, V.: Základní informace o bázi BALEX. Československá informatika, 11, 1988, s. 330–333.
Šteinfeldt, E.: Častotnyj slovar’ russkogo jazyka. Tallin 1963.
Těšitelová, M.: Otázky lexikální statistiky. Praha 1974.
Těšitelová, M.: Využití statistických metod v gramatice. Praha 1980.
Těšitelová, M. (ed.): Frekvenční slovník češtiny věcného stylu. Praha 1983.
Thorndike, E. L. – Lorge, I.: The Teachers Word Book of 30 000 Words. New York 1972.
Valouch, V.: Vztahy mezi pořadím a četností kódových znaků (slov). Praha 1970. Diplomová práce.
Voronin, J. A.: Teorija klassificirovanija i jeje priloženija. Novosibirsk 1985.
Zipf, G. K.: Human Behaviour and the Principle of Least Effort. Cambridge, Mass. 1949.
R É S U M É
A contribution to objectifying semantic classes
This article attempts to distribute 2000 most frequent Czech words (according to the dictionary Jelínek – Bečka – Těšitelová) into particular semantic fields. The starting point of this distribution is Roget’s Thesaurus.
The Czech set was compared with a similar set of English and Russian words and striking similarities among them were discovered. It is obvious that semantic features of the most frequent words are interlingual.
Since the system of semantic fields presented in my article is quite small (consisting of only 32 fields) it is greatly efficient.
It is especially noteworthy that 2000 most frequent words chosen fulfil within certain bounds Zipf’s rank–size theorem. Furthermore I demonstrate that even if I distribute these words into 32 semantic subsets and rank them on the descending scale of frequency the lists obtained also fulfil to some degree the rank–size theorem. Additional corroboration of my hypothesis on greater data is necessary to prove it beyond any reasonable doubt.
Slovo a slovesnost, volume 53 (1992), number 1, pp. 23-32
Previous Bronislava Volková: K emotivní sémantice a sémiotice
Next Milada Hirschová: Neurčitost komunikačních funkcí ve spontánních mluvených projevech
© 2011 – HTML 4.01 – CSS 2.1