
O jednom algebraickém modelu jazyka
Ladislav Nebeský
[Articles]
Об одной алгебраической модели языка / A propos d’un modèle algébraïque de la langue
1. Algebraickou lingvistiku (dále jen AL) lze dělit na dvě části: syntetickou a analytickou (obvyklejší je rozlišovat syntetické a analytické modely jazyka).[1] Rozdíl mezi syntetickou a analytickou algebraickou lingvistikou je patrný na přístupu k větám.[2]
Syntetická AL si klade za úkol formálními prostředky vymezit, které (konečné) řetězy slovních tvarů jsou větami. K tomuto cíli směřují dva druhy procedur: rekognoskativní a generativní. Rekognoskativní procedura (rozvinutá hlavně v tzv. kategoriální gramatice),[3] slouží k rozhodnutí o každém jednotlivém řetězu slovních tvarů, je-li větou či nikoli. V jistém protikladu k ní stojí procedura generativní (reprezentovaná zejména gramatikami Chomského),[4] jejímž úkolem je všechny (ale právě jenom ty) řetězy slovních tvarů, které jsou větami, zkonstruovat. Ke každé rekognoskativní proceduře lze definovat generativní (proto řazení kategoriální gramatiky k rekognoskativním procedurám není přesné, tuto gramatiku lze formulovat též jako proceduru generativní, srov. Bar-Hillel (o. c. v pozn. 3); naproti tomu ne ke každé generativní proceduře lze najít rekognoskativní (rozumí se takovou, která bude za věty považovat právě ty řetězy, které generativní procedura konstruuje). To tedy znamená, že generativní procedura stojí nejenom v jistém protikladu k rekognoskativní, ale zároveň je procedurou mohutnější. Zdůrazněme, že je rozdíl mezi generativní procedurou vůbec a mezi pravidly Chomského gramatik, které ji v AL nejčastěji reprezentují. Obecně vzato, pravidla Chomského jsou pouze jedním z možných postupů ke generování vět. Jinými jsou např. vyvozovací pravidla různých logických kalkulů; možnost ještě jiných generujících pravidel bude naznačena v tomto příspěvku.
Analytická AL v protikladu k syntetické vychází ze znalosti (přesněji danosti) všech vět jazyka a studuje ty vztahy mezi slovními tvary nebo obecně řetězy slovních tvarů, které se větami jazyka dají definovat.[5] První rozpracoval [232]metodu analytické AL Bar-Hillel.[6] S podobnou myšlenkou přichází O. Kulaginová (o. c. v pozn. 5); na ni navazuje několik sovětských badatelů.[7]
Srovnáním prací ze syntetické a analytické AL lze dojít k názoru, že jde o dvě protikladné stránky téhož. Na těsnou souvislost mezi modely syntetickými a analytickými upozorňuje např. Revzin (viz pozn. 7) a Čulík.[8] V tomto článku se pohled na syntetickou a analytickou AL prolíná, syntetické a analytické jsou jenom dva různosměrné přístupy k témuž.
2. Budeme předpokládat, že je dána nějaká konečná neprázdná množina L, jejíž prvky budeme interpretovat jako slovní tvary. Symbolem N označíme množinu všech (konečných) řetězů nad množinou L (včetně prázdného řetězu, který označíme I). Tak např. kdyby množina L obsahovala symboly (v naší interpretaci slovní tvary) a a b, bude množina N obsahovat mimo jiné řetězy: I, a, b, ab, ba, aa, bb, aaaaaa, ababab, bbaaaba atd. Z toho, že množina L je konečná neprázdná, vyplývá, že množina N je spočetně nekonečná.[9]
Naším prvním úkolem bude definovat dvě nekonečné posloupnosti jistých typů množin řetězů slovních tvarů z L. Budeme-li nějakou množinu řetězů slovních tvarů považovat za množinu vět konkrétního jazyka a bude-li této množině přiřazen některý z definovaných typů, přiřadíme týž typ i jazyku. Zadání typů množin lze jednoznačně zařadit do analytické části AL. Považujeme-li totiž uvažovanou množinu řetězů za množinu vět nějakého jazyka, splňuje se základní předpoklad analytické AL, tj. předpoklad, že množina vět jazyka je předem známa. Této množině se potom přiřadí typ (je-li to ovšem možné) v závislosti na jistých syntaktických vlastnostech této množiny.
Dříve než budeme první posloupnost typů definovat obecně, budeme zvlášť definovat první člen této posloupnosti. Řekneme, že nějaká množina A, která je podmnožinou množiny N, je typu U1, když pro každou trojici řetězů α, β, γ z N (tedy i prázdných) a pro každou čtveřici slovních tvarů x0, x1, y0, y1 z L platí: Jsou-li řetězy αx0βy0γ, αx0βy1γ, αx1βy0γ elementy z A, je také řetěz αx1βy1γ elementem množiny A. První tři řetězy v této definici budeme nazývat výchozími, poslední řetězem výsledným. Platí tedy: Patří-li do množiny A první tři výchozí řetězy a je-li množina A typu U1, patří do množiny A i řetěz výsledný.
Letmý pohled na češtinu nás přesvědčí, že se od jazyka typu U1 odchyluje v mnoha bodech. Budeme si všímat jen jednoduchých vět. Zvolme např. x0 = kouřící, x1 = mladý, y0 = muž, y1 = žena, α, β jsou prázdné, γ = sedí. Vidíme, že ačkoli řetězy kouřící muž sedí, kouřící žena sedí, mladý muž sedí jsou české věty, řetěz mladý žena sedí českou větou není. Jiný příklad je tento: x0 = tašku, x1 = čerstvé, y0 = ovoce, y1 = brambor, γ = přinesl, α, β jsou prázdné. Opět vidíme, že ačkoli přinesl tašku ovoce, přinesl čerstvé ovoce, přinesl tašku brambor jsou české věty, řetěz přinesl čerstvé brambor českou větou není. Lze říci, že čeština se díky své flektivnosti a jiným nepravidel[233]nostem značně vymyká typu U1. Je nesporné, že podrobným studiem toho, kde se vymyká a proč, lze dojít k zajímavému rozboru homonymie.[10]
Neshoda s typem U1 není však výsadou češtiny. Dosadíme-li x0 = I, x1 = he, y0 = may, y1= go, α, β, γ necháme prázdné, vidíme, že ačkoli I may, I go, he may jsou anglické věty, řetěz he go do angličtiny nepatří. Rozhodně se zdá, že jazyky flektivní odporují typu U1 nejvíce, aglutinační nejméně. Podrobná diskuse o vztazích mezi typy z typologie jazyků a typem U1 by byla jistě plodná a žádoucí.
Prvním zobecněním typu U1 je typ U2. Řekneme, že množina řetězů A je typu U2, když pro každé řetězy α, β, γ, δ a každé slovní tvary x0, x1, y0, y1, z0, z1 platí: Jsou-li αx0βy0γz0δ, αx0βy0γz1δ, αx0βy1γz0δ, αx0βy1γz1δ, αx1βy0γz0δ, αx1βy0γz1δ, αx1βy1γz0δ elementy množiny A, je také řetěz αx1βy1γz1δ elementem množiny A. Je-li množina A typu U1, snadno zjistíme, že je také typu U2 (tzn. že není-li množina A typu U2, nemůže být ani typu Ul), typ U2 je tedy obecnější.
Neshoda češtiny s typem U2 se zjišťuje daleko hůře; pokud se objevuje, jde o případy komplikovaně skloubené homonymie. Zhruba lze říci, že je možno takové případy nalézt daleko snáze u krátkých vět, nejsnáze pak v případě, kdy řetězy α, β, γ, δ z definice typu U2jsou prázdné (tzn. u vět skládajících se ze tří slovních tvarů). Ale i zde byly prozatím nalezeny pouze takové případy, jejichž výjimečnost v syntaktickém systému češtiny je více než nápadná. Dosaďme: x0 = nos, x1 = nosem, y0 = je, y1 = sestřenici, z0 = nos, z1 = připraven. Řetězy nos je nos, nos je připraven, nos sestřenici nos, nos sestřenici připraven, nosem je nos, nosem je připraven, nosem sestřenici nos jsou českými větami, ale řetěz nosem sestřenici připraven českou větou není. Zdá se, že má čeština k jazykům typu U2 velmi blízko. V každém případě však bude k prověření nutný podrobnější rozbor.
Definovali jsme dosud typ U1 a typ U2. Nyní budeme definovat obecně typ Un pro každé celé kladné číslo n. Řekneme, že množina řetězů slovních tvarů je typu Un, když pro každé řetězy slovních tvarů α0, …, αn+1 a každé slovní tvary x00, …, xn0, x01, …, xn1 platí: Jsou-li řetězy α0x0i0α1 … αnxninαn+1 prvky množiny A pro každé indexy i1, … in takové, že i0 + … + in < 2n + 2, je také α0x01α1 … αnxn1αn+1 elementem množiny A. Snadno se přesvědčíme, že předchozí dvě definice byly speciálními případy této definice obecné. Všimněme si, že v definici typu Un je vždy 2n+1 — 1 řetězů výchozích a vždy jeden výsledný. Počet výchozích řetězů s rostoucím n rychle stoupá. Tak např. pro n = 3 a 4 je 15 a 31 výchozích řetězů. Tedy prověřování toho, je-li jazyk jazykem nějakého vyššího typu, je obtížné.
Může se vyskytnout otázka, má-li smysl definovat celou nekonečnou posloupnost typů Un. Viděli jsme, že čeština není sice jazykem typu U2, ale že se od něho odlišuje patrně jen v okrajových případech. Je nasnadě se domnívat, že srovnání češtiny s typem U3 dopadne ještě daleko příznivěji (máme na mysli stále jen jednoduché věty). Skutečně se zdá, že v praxi vystačíme s velmi malým počtem typů. Protože však nevíme přesně s kolika typy skutečně vystačíme (a protože s vyššími nároky na úplnost popisu přirozeného jazyka by asi i počet uvažovaných typů o něco stoupl), je vhodnější (a teoreticky vlastně jednodušší) definovat typ Un pro libovolné kladné celé číslo n.
Snadno se lze přesvědčit přímo z definice typů Un, že typ s vyšším pořadovým číslem je zobecněním typů s pořadovým číslem nižším. Tak např. je-li množina A typu U1, je tím spíše typu U2 a typu U3 atd. A naopak: Zjistíme-li, že množina A není typu U3, není tím spíše typu U2, tím spíše typu U1 atd.[11] Tuto posloupnost typů lze dále zobecnit. Zobecněním pak dojdeme k definici typů množin Vn. Definice těchto nových typů budou obměnou definice typu Un. V definici typu Un se operuje se [234]slovními tvary x00…, x1n. K typu Vn dojdeme, budeme-li v definici místo slovních tvarů uvažovat jakékoli řetězy slovních tvarů (včetně prázdného, tj. všechny prvky množiny N). To tedy znamená, že množina řetězů slovních tvarů A je typu Vn, když pro každé α0, …, αn+1 z N a každé ξ00, …, ξn0, ξ01 …, ξn1 z N platí: Jsou-li αξ0i0α1 … αnξninαn+1, pro i0 …, in, pro něž platí i0 + … + in < 2n + 2, elementy z A, je také řetěz α0ξ01α1 … αnξn1αn+1 elementem množiny A. Z definice vyplývá, že je-li množina A typu Vn, je také typu Un pro všechna celá kladná čísla n.
Na základě toho lze dokázat následující tvrzení: Je-li libovolný systém množin typu Un (respektive Vn), je také množina, která je průnikem tohoto systému množin, stejného typu. Odtud dále plyne, že pro libovolnou množinu řetězů slovních tvarů A lze najít právě jednu takovou množinu B, pro níž platí: 1. množina B je typu Un (respektive Vn); 2. množina B je nadmnožinou množiny A; 3. žádná množina různá od množin A a B, která je zároveň nadmnožinou množiny A a podmnožinou množiny B, není typu Un (respektive Vn). To tedy neznamená, že k libovolné množině A lze najít právě jedinou její nadmnožinu (která pochopitelně množině A může být rovna), která je množinou typu Un (respektive Vn) a která je ze všech nadmnožin množiny A, které jsou téhož typu, nejmenší. Jestliže tuto množinu označíme jako un(A) (respektive vn(A)), máme tak definovány dvě nekonečné posloupnosti předpisů (zobrazení), přiřazujících každé množině řetězů nějakou (jinou nebo i stejnou) množinu řetězů.
Zobrazení u1, u2, …, v1, v2, … splňují jisté teoreticky závažné vlastnosti; díky těmto vlastnostem jsou definovaná zobrazení jednak U-topologií,[12] jednak konečnou konsekvencí.[13] Mimo to pro každou množinu řetězů A platí ul(A) ⊃ u2(A) ⊃ u3(A) …, v1(A) ⊃ v2(A) ⊃ …; dále platí un(A) ⊂ vn(A), pro každé celé kladné číslo n. Kromě toho platí pro každé n: Je-li množina řetězů A konečná, je množina un(A) rovněž konečná. Toto tvrzení pro zobrazení vn neplatí.
Jak jsme již ukázali, definice typů jazyků Un, Vn patří do analytické AL, naproti tomu definice zobrazení un, vn patří do AL syntetické, neboť slouží jako prostředek k zkonstruování množin řetězů slovních tvarů (jistých předepsaných vlastností). Na tato zobrazení lze hledět jako na rekurentní pravidla, která — aplikujeme-li je na nějaký výchozí repertoár vět — generují věty jazyka předepsaného typu. Tak např. nechť A je nějaká (třeba konečná) množina vět jazyka, jehož všechny věty tvoří množinu v1(A). Tuto množinu lze definovat takto:
a) Všechny řetězy z množiny A jsou větami jazyka.
b) Jsou-li α, β, ξ, ξ', ζ, ζ' libovolné řetězy slovních tvarů a jsou-li řetězy αξβζγ, αξβζ' γ, αξ' βζγ větami jazyka, je také řetěz αξ' βζ' γ větou jazyka.
Pravidlo b) lze podstatně zjednodušit (tohoto postupu lze však užít jen pro vn, nikoli un): Jsou-li ξ, ξ', ζ, ζ' libovolné řetězy a jsou-li řetězy ξζ, ξζ', ξ'ζ větami jazyka, je také řetěz ξ'ζ' větou jazyka.
Vyšli jsme tedy z definice typů jazyků (které patří do analytické AL) a dospěli k definici předpisů, které z nějaké výchozí množiny vět jazyka všechny věty jazyka konstruují (ty zase patří do syntetické AL a lze je chápat jako generativní procedury). Mohli jsme zvolit i cestu opačnou — vyjít z definice zobrazení a dojít k typům. Tato cesta je stejně možná. Tak např. typ Un tvoří všechny takové množiny řetězů A, pro něž platí A = un (A).
Máme tedy dvě posloupnosti prostředků pro generování řetězů slovních tvarů. Vzniká otázka, lze-li se na ně dívat jako na generativní gramatiky schopné generování vět přirozených jazyků. Zobrazení un jsou zřejmě pro libovolně velká n k sa[235]mostatnému generování jazyka příliš slabá. Jak jsme již uvedli, pro libovolnou konečnou množinu platí, že z ní nelze použitím těchto zobrazení zkonstruovat množinu nekonečnou. Tím ovšem není řečeno, že by tato zobrazení byla z tohoto hlediska bezcenná. Lze jich použít tehdy, chceme-li množinu vět rozšířit tak, aby výsledná množina nebyla příliš mohutná, ale měla pravidelnější strukturu. Jde tedy o jakési „zaokrouhlení“ množiny vět na základě analogií v jejich struktuře (dále viz odst. 3).
Naproti tomu zobrazení vn je už spíše možno chápat jako generativní gramatiku, protože s jeho pomocí lze zkonstruovat z konečného počtu zadaných řetězů množinu řetězů, která může být nekonečná. Všimneme si z této stránky pouze zobrazení v1. Uvedeme několik případů jednoduchých formálních jazyků, které lze generovat zobrazením (gramatikou) v1.
Nechť množina L obsahuje symboly — vlastně slovní tvary — a, b, c. Jako J1 označíme jazyk skládající se z řetězů abn, kde n = 0, 1, 2, … (tj. z řetězů a, ab, abb, abbb, …); jako J2 označíme jazyk skládající se ze všech možných řetězů nad symboly a a b, včetně prázdného řetězu, tzn. že do J2 patří např. řetězy: I, a, b, ab, ba, aba, bab, aab, baa, abb, bba, …): jako J3 označíme jazyk skládající se z řetězů amban, kde m, n = 0, 1, 2, … (tj. z řetězů b, ab, ba, aba, aaba, abaa, …); jako J4 označíme jazyk skládající se z řetězů amcbn, kde m, n = 0, 1, 2, … (tj. z řetězů c, ac, cb, acb, …); jako J5 označíme jazyk skládající se z řetězů abmcabn, kde m, n = 0, 1, 2, … (tj. z řetězů aca, abca, acab, abcab, …). Každý z těchto pěti jazyků se skládá z nekonečného počtu řetězů; každý z nich je možno generovat gramatikou v1 z konečného počtu řetězů.
Všimneme si nejdříve jazyka J1, pro nějž platí: J1 = v1 ({a, ab}).[14]
Na podrobný důkaz tohoto tvrzení zde není místa. Ale vezměme si libovolný řetěz abn z J1, např. ab4 (rozepsáno: abbbb), a ukažme, že jej lze odvodit gramatikou v1 z řetězů a a ab. Jak již bylo řečeno, je-li A množina řetězů, lze množinu řetězů vl(A) definovat takto: 1. A je častí v1(A). 2. Jsou-li ξ, ξ', ζ, ζ' řetězy, platí: Patří-li řetězy ξζ, ξζ', ξ'ζ do množiny v1(A), je také řetěz ξ, ζ prvkem množiny v1(A). Podmínku 2. zapíšeme:
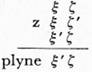
Tohoto schématu použijeme k znázornění postupu při generování (odvození) řetězu abbbb. Jak je vidět z obecného pravidla pro generování touto gramatikou, je nutno každý řetěz pomyslně rozdělit na dvě části (mohou je tvořit i prázdné řetězy). Pro větší názornost toto pomyslné dělení naznačíme mezerou. Tak např. řetěz ab bude se v průběhu odvozování zvoleného řetězu dělit dvěma způsoby. V schématu odvozování se objeví jako a b a ab I. Odvozování vypadá takto:
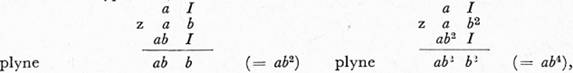
žádaný řetěz je tedy odvozen.
O jazyku J2 platí: J2 = v1 ({I, a, b,}).
Na ukázku odvodíme řetěz abbab:
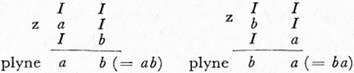
[236]
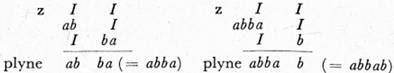
O jazyku J3 platí: J3 = v1 ({b, ab, ba}).
Na ukázku odvodíme řetěz aaba:
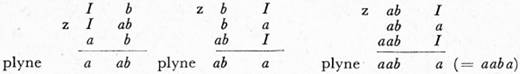
Dále platí: J4 = v1 ({c, ac, ca}), J5 = v1 ({aca, abca, acab}).[15]
Při srovnání s jinými generativními gramatikami zjistíme, že gramatika v1 je velmi slabá, tj. že mnohé jazyky, které lze generovat jinými gramatikami, gramatikou v1 generovat nelze. Vezměme např. gramatiku s konečným počtem stavů, která je z frázových gramatik N. Chomského nejslabší. Touto gramatikou je např. možno generovat jazyk J6 = {ambn, m, n = 0, 1, 2, …}. Tento jazyk však nelze definovat gramatikou v1. (To znamená, že neexistuje žádná konečná množina A taková, aby v1 (A) = {ambn, m, n, = 0, 1, 2, …}).
Zásadní příčina malé účinnosti gramatiky v1 spočívá v tom, že se při její aplikaci nepoužívá žádných pomocných symbolů. Gramatiku v1 (stejně jako všechny gramatiky vn) lze různým způsobem adaptovat tak, aby používala symbolů dvojího druhu, čímž se zvýší její účinnost.
Naznačíme jeden možný způsob adaptace gramatiky v1. Předpokládejme, že L neobsahuje symbol *. Symbolem N* označíme takové řetězy, které 1. začínají symbolem * a 2. obsahují symboly z L nebo *.
Jestliže L = {a, b, c}, patří do N*, např.: *, *a, **a, *abab, *c*a*bba atd. Řetězy z N budeme nazývat vlastními, řetězy z N* pomocnými.[16] Gramatiku v1 budeme nyní aplikovat pouze na řetězy pomocné. Generativní proces adaptované gramatiky — označíme ji v* — se bude skládat ze dvou kroků: 1. z aplikace gramatiky v1 na množinu pomocných řetězů (výsledkem bude zase množina pomocných řetězů); 2. vypuštění pomocného symbolu ze všech pomocných řetězů, a tudíž přechod k řetězům vlastním.
Gramatikou v* lze generovat jazyk J6, pro nějž platí: J6 = v* (**, *a*, **b), neboť v1 (**, *a*, **b) = {*am*bn, m, n, = 0, 1, 2, …} a vypuštěním symbolu * dostáváme množinu řetězů {ambn, m, n = 0, 1, 2, …}, což je jazyk J6.
Jak již bylo uvedeno, gramatika v* je jen jednou z možných adaptací gramatiky v1, které se opírají o pomocné symboly přidané k vlastním slovním tvarům jazyka. Je však i jiná cesta zobecnění. Její úplný a přesný popis je značně složitý, zde se omezíme jen na přibližný výklad její podstaty. Vyjdeme ze schématu, které jsme užívali při aplikaci v1 na s. 235:
Vystupují tu čtyři řetězy (ξζ, ξζ', ξ' ζ, ξ' ζ'), každý dělený na dvě části. Zřetězením (tj. spojením za sebou) těchto částí dostaneme dělený řetěz. K zobecnění dojde[237]me, když místo zřetězení připustíme libovolnou kompozici. Způsob kompozice musí být potom naznačen v řetězech ξ, ξ', ζ, ζ', např. pomlčkou.
Vezměme tento příklad:
Nechť ξ = I; rozdělíme jej na dvě části I — I; za ξ' položme řetěz ab; také ten rozdělíme na dvě části: a — b; jako ζ zvolme c a jako ζ' řetěz abc; tyto řetězy dělit nebudeme. Jejich kompozici provedeme tak, že vezmeme první část prvého řetězu (např. ξ), k ní zprava připíšeme první část druhého řetězu (např. ζ), k ní opět druhou část prvního řetězu atd., dokud je co připisovat (v našem příkladu jsme již hotovi). Označíme-li proces kompozice jako x, můžeme psát:

Uvedli jsme pouze náčrt možného zobecnění v1, který — spojí-li se s některou z uvedených adaptací — vede k tzv. kompoziční gramatice, která již obstojí v srovnání s frázovými gramatikami.
3. V tomto článku jsme si vzali za úkol nastínit problematiku jisté části AL. Vyšli jsme z přístupu analytického a poté přešli k stránce syntetické, přesněji řečeno generativní. Jde o oblast AL, v níž je dosud mnoho nevyřešených otázek, jak algebraických, tak i lingvistických. Na některé z nich jsme upozornili výše. Nakonec si všimněme ještě jedné.
Na začátku odst. 2 jsme definovali typy jazyků Un. Řekli jsme, že je pravděpodobné, že se čeština — bereme-li v úvahu pouze věty jednoduché — liší od typu U2 jen nepodstatně. Je možné, že to platí i o většině ostatních přirozených jazyků (některé z nich se budou už od typu U1 lišit méně než čeština). Není proto pravděpodobné, že by zařazení jazyků do typů Un přineslo něco pro jazykovou typologii. Tím spíše by však typy Un ukázaly na to, co mají přirozené jazyky společného.
Množina (gramaticky správných) vět jazyka je zřejmě naší abstrakcí, vzniklou z množiny těch řetězů slovních tvarů, jimiž se lze běžně dorozumět (které — použity v kontextech, jež považujeme za možné — mají smysl). Tato abstrakce musí být pochopitelně založena na analogiích ve stavbě řetězů slovních tvarů. Shodneme-li se pro jednoduchost na tom, že přirozené jazyky — množiny jednoduchých vět těchto jazyků — jsou typu U2, lze položit otázku, zda zobrazení u2 (jehož definice je rovněž založena na analogiích ve struktuře výchozích řetězů) nám zmíněnou abstrakci nemodeluje. Tento problém je značně složitý a k jeho rozřešení by jistě byla nutná spolupráce lingvisty, matematika a psychologa, nicméně typy Un (respektive Vn) k jeho řešení naznačují cestu.
R é s u m é
ON AN ALGEBRAIC MODEL OF LANGUAGE
On the basis of the properties of sentences of language two infinite sets of types of languages Un and Vn are defined. By means of them we proceed to define the mappings un and vn which associate an over-set to every set of strings over a finite set of word-forms. These mappings fulfil the properties of U-topology (see footnote 12) and finite consequence (see footnote 13). The study examines the relation of the types Un with natural languages. The possibility of using a certain adopted form of the mappings vn (v* described here into more detail) as a generative grammar is discussed.
[1] Srov. I. I. Revzin, Modely jazyka, Moskva 1962; ref. K. Berky a P. Nováka v SaS 24, 1963, 133—140.
[2] Jak je v AL obvyklé, budeme se na věty jazyka dívat jako na útvary, jež lze jednoznačným (předem známým) způsobem rozložit na útvary nižší (slovní tvary), jejichž strukturu již dále neanalyzujeme. Toto schéma je pochopitelně jednostranné, z teoretického hlediska však závažné. K hlubšímu modelu věty dojdeme stěží přes jeho popření; takový model zřejmě musí toto schéma pojmout do sebe jako svou část.
[3] Viz K. Ajdukiewicz, Język i poznanie. Warszawa 1960; Y. Bar-Hillel — C. Gaifman — E. Shamir, On Categorical and Phrase Structure Grammars, Bull. of Research Council Of Israel, Vol 9F, 1-16, Jerusalem 1960; J. Lambek, The Mathematics of Sentence Structure, Am. Math. Monthly, 1958, 65, 154n.; J. Lambek, On Calculus of Syntactic Types, Proc. of Symp. in Applied Mathematics, Vol XII, 166n.; z poněkud jiné strany též H. B. Curry, Combinatory Logic, Amsterodam 1958 a Some Logic Aspects of Grammatical Structure, Proceedings of Symposia in Applied Mathematics, Structure of Language and its Mathematical Aspects, Vol XII, 56n., 1961.
[4] N. Chomsky, Three Models for the Description of Languages, IRE Transactions on Information Theory, September 1956, 113—124; N. Chomsky, Syntactic Structures, s’ Gravenhage, 1957; N. Chomsky, On Certain Formal Properties of Grammars, Information and Control, 1959, 137—167.
[5] Některé práce z této oblasti, např. O. S. Kulagina, Ob odnom sposobe opredelenija grammatičeskich ponjatij na baze teorii množestv, Problemy kibernetiki, Moskva 1956, vycházejí i z vlastností dalších („paradigmatických“); ty jádro analytické AL netvoří a pomineme je.
[6] Viz Y. Bar-Hillel, On Syntactic Categories, Journal Symb. Logic, 1950, 1—16.
[7] Viz např. I. I. Revzin, Nekotoryje voprosy formalizacii sintaksisa, B. Mašinnogo perevoda 1957, 5n.; Ustanovlenije sintaksičeskich svjazej v MP metodom Ajdukieviča — Bar-Hillela i v terminach konfiguracionnogo analiza, Doklady na konferecii po obrabotke informacii, mašinnomu perevodu i avtomatičeskomu čteniju teksta 2, Moskva 1961, cit. Modely jazyka; R. L. Dobrušin, Elementarnaja grammatičeskaja kategorija, Matematičeskoje prosveščenije 5, 1961, 19n.; V. A. Uspenskij, K opredeleniju časti reči v teoretiko-množestvennoj sisteme jazyka, BMP 5, 1957.
[8] K. Čulík, referát na čs. kybernetické konferenci v Praze 1962.
[9] Spočetně nekonečné jsou takové množiny, jejichž prvky lze očíslovat přirozenými (tj. celými kladnými) čísly. Ostatní nekonečné množiny se nazývají nespočetné. Např. množina iracionálních (nebo všech reálných) čísel je nespočetná.
[10] Prvním pokusem o takový rozbor je referát I. Kalendové Gramatická konsekvence, ref. na studentské vědecké konferenci v Olomouci 1963.
[11] Stačí v definici typu Un+1 položit x0n+1 = x1n+l; potom je αn+1x0n+1αn+2 = αn+1x1n+1αn+2; píšeme-li místo tohoto řetězu αn+1, dospíváme k definici typu Un.
[12] E. Čech, Topologické prostory, Časopis pro pěstování matematiky, 1937, 235n.
[13] T. Kubinski, O zasięgu twierdzenia Lindenbauma o nadsystemach zupelnych, Studia Logica 12, 1961, 83n.
[14] Symbolicky zapsanému výroku J1 = v1 ({a, ab}) nutno rozumět takto: Všechny řetězy jazyka J1 (a právě jenom ty) lze dostat, aplikujeme-li zobrazení v1 na dvouprvkovou množinu skládající se z řetězů a a ab.
[15] Důkazy těchto pěti identit by se vymykaly možnostem tohoto článku. Poznamenejme jen, že dokazuje-li se identita tvaru J = v1(A), je nutno nejen prověřit, že každý řetěz jazyka J je odvoditelný z množiny A, ale také dokázat, že aplikací zobrazení v1 na množinu A nemůžeme dojít k žádnému řetězu, který by byl vně jazyka J.
[16] Protože symbol * neleží v množině L, není množina N* částí množiny N, nýbrž je s ní disjunktní. Žádný řetěz tedy nemůže být současně vlastní a současně pomocný.
Slovo a slovesnost, volume 24 (1963), number 4, pp. 231-237
Previous Zdenka Palková: K rytmu v české próze (Na materiálu z prózy Vl. Vančury)
Next Otto Ducháček: Různé typy významových vztahů a problematika jazykových polí
© 2011 – HTML 4.01 – CSS 2.1